江苏省海中学高一期中调研试卷

　　　　　　 数学试题　　　　 2005.11.

（本试卷满分150分，考试时间为120分钟）

一．选择题（每小题5分，满分60分。把答案填在答题纸上相应的表格中）

1．下列四个关系式中，正确的是　　　　　　　　　　　　　　　 （　 ）

A. 　　 B.　　C.　 D.

2.集合A={ x x = y, y∈R}，B={yy=x², x∈R}则A∩B= 　　　　　　( 　)

　　A. {0 , 1}　　　　 B. {(0 , 1)}　　　　C. {yy≥0}　　　 D.

3．下列各组函数中，表示同一函数的是　　　　　　　　　　　　  ( 　)

　 A 　　　　　　　 B

C 　　　　　　D

4．下列几个图形中,可以表示函数关系y=f(x)的那一个图是　　　　  (　 )

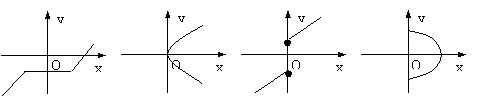
　　　　 A 　　　　　　　　B　　　　　　　　 C　　　　　　  D

5、若a=0.3²，b=log₂0.3，c=2^0.3，则a、b、c的大小关系是　　　　 （　 ）

A、a<c<b　　　B、a<b<c　　　C、b<a<c　　　　  D、b<c<a

6．　　　 （　 ）

A　有最大值，但无最小值　　　B　有最小值，有最大值1

C 有最小值1，有最大值 　　 D　无最大值，也无最小值

7．函数y=的定义域为　　　　　　　　　　　　  （　 ）

A．（，+∞） B．［1，+∞　C．（ ，1 D．（－∞，1）

8．函数y=是　　　　　　　　　　　　　　　　　 （　 ）

A．奇函数　　　　　　　　　　　  B．偶函数　

C．既是奇函数又是偶函数　　　　　 D．非奇非偶数　

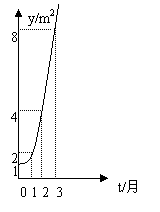9.如图所示的是某池塘中的浮萍蔓延的面积()与时间(月)

的关系:,有以下叙述:① 这个指数函数的底数是2;

② 第5个月时,浮萍的面积就会超过;

③ 浮萍从蔓延到需要经过1.5个月;

④ 浮萍每个月增加的面积都相等;

⑤ 若浮萍蔓延到、、所经过的时间

分别为、、，则.

y

其中正确的是　　　　　　　　　　　　　　　　　　　　　　　　 (　　)　　　　　　　　　　　　　　　　　　　　　　　　　　

　 A. ①②　　　　  B.①②③④　　　　C.②③④⑤　　　  D. ①②⑤

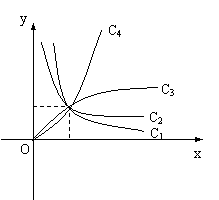10.如图, 给出幂函数y=xⁿ在第一象限内的图象 , n取±2 , ±四个值, 则相应于曲线C₁ , C₂ , C₃ , C₄的n依次为　　　　　　　　　　　　　　　　　(　  )

　　　　　　　　　　　　　　　　　　　　　

　 A. －2 , － ,  , 2、B. 2 ,  , － , －2

C. － , －2 , 2 , 、D. 2 ,  , －2 , －

11． 方程根的情况是　　　　　　　　　　　　　　　  （　　）

A.有两个正根　　　　　　 B.一个正根一个负根

C.有两个负根　　　　　   D.仅有一个实数根

12.已知偶函数f(x)在(－∞,0)上单调递增，对于任意x₁<0,x₂>0,

若∣x₁∣<∣x₂∣,则有　　　　　　　　　　　　　　　　　　　　  （　　）

A.f(－x₁)> f(－x₂)　　　　　　　 B.f(－x₁)﹤ f(－x₂)

C.－f(－x₁)> f(－x₂)　　　　　　 D.－f(－x₁)﹤ f(－x₂)

二．填空题（每小题4分，满分16分。把答案填在答题纸上的相应横线上）

13．已知函数，则的值是　　　　　 

14．已知且则=　 -13　　　　

15.若函数在上是增函数,则实数的取值范围是　　　　　　　　　   .

16. 关于函数有以下4个结论:其中正确的有　　　　　 　

　① 定义域为　 ② 递增区间为

③ 最小值为1;　　　　　　　　  ④ 图象恒在x轴的上方

三．解答题（6个小题，满分74分）

17．（满分12分）

若集合，

且，求实数、b的值；

18. （满分12分）

（1）计算：0.25^－1×(+log₂(₎×log₃()×log₅()

（2）已知：lg（x－1）+lg（x－2）=lg2，求x的值

19．（满分12分）

设二次函数f(x)满足：①f(x－2)= f(－x－2);②它的图象在y轴上的截距为1；③它的图象在x轴上截得的线段长为2。试求f(x)的解析式。

20．（满分12分）

设函数,

(1)　  求证:不论为何实数总为增函数;

(2)　  确定的值,使为奇函数及此时的值域.

21．（满分12分）

季节性服装当季节即将来临时，价格呈上升趋势，设某服装开始时定价为10元，并且每周(7天)涨价2元，5周后开始保持20元的价格平稳销售；10周后当季节即将过去时，平均每周削价2元，直到16周末，该服装已不再销售。

（1）试建立价格P与周次t之间的函数关系式。

（2）若此服装每件进价Q与周次t之间的关系为Q＝－0.125(t－8)²＋12，

t∈[0，16]，t∈N^*，试问该服装第几周每件销售利润L最大?

（注：每件销售利润＝售价－进价）

22. （满分14分）

已知函数,当时,恒有.

(1). 求证:

(2). 若试用表示

(3). 如果时,且,试求在区间上的最大值和最小值.

命题：李建华  

校对：李建华

　　　　　　　　　　　　　　　　　　　  附答案

江苏省海安中学高一期中调研试卷

一．选择题（每小题5分，满分60分。把答案填在下面的表格中）

1	2	3	4	5	6	7	8	9	10	11	12
D	C	C	A	C	C	C	B	D	A	D	A

二．填空题（每小题4分，满分16分。把答案填在下面的横线上）

13 　　　1/9　　　　　　　 　　 14 　　　　-13　　　　　　   

15 　　　a≥3　　　　　　　 　　16 　　 ②③④　　　　　　 

三．解答题（6个小题，满分74分）

17. 解析:

若;

若;

若B=.

18（1）0

　（2）x=3

19.f(x)=0.5x²+2x+1

20 (1) 的定义域为R, ,

则=,

, ,

即,所以不论为何实数总为增函数.

　　　　 (2) 为奇函数, ,即,

　　　　　  解得:  

(3)　   由(2)知, ,,

　　

　　　 所以的值域为

21.　　　　　　　  　　　10+2t　 t∈[0,5]

 (1)　　P=　　20　　t∈(5,10]

　　　  20-2t　 t∈(10,16]

 (2)二次函数最值3种情况分别求

22: (1)令得,再令得

(2)由.

(3)设,则=

,,

在R上是减函

数,,

.