江苏省南通中学2005—2006学年度第一学期期中考试
高一数学试卷
（时间120分钟，满分100分）
第I卷
一、 选择题：（每小题3分，共12小题，合计36分）
1、 下列几个关系中正确的是（ ）
A、
B、 
C、
D、
2、设
是集合M到集合N的映射，下列说法正确的是（ ）
A、 M中每一个元素在N中必有输出值。
B、 N中每一个元素在M中必有输入值。
C、 N中每一个元素在M中的输入值是唯一的。
D、 N是M中所有元素的输出值的集合。
3、下列函数与
有相同图象的一个是（
）
A、
B、
C、
且
D、
且
4、集合
，则（
）
A、
B、
C、
D、
5、已知
且
，则
的值为（
）
A、19 B、 13 C、 -19 D、 -13
6、若
，则函数
的图象必过点（
）
A、
B、（0，0） C、（0，-1） D、（1，-1）
7、要得到函数
的图象，只需将函数
的图象（
）
A、 向右平移2个单位，向下平移1个单位。
B、 向左平移2个单位，向下平移1个单位。
C、 向右平移2个单位，向上平移1个单位。
D、 向左平移2个单位，向上平移1个单位。
8、定义集合A、B的一种运算：
，若
，
，则
中的所有元素数字之和为（
）
A．9 B. 14 C.18 D.21
9、已知函数
在区间（-1，1）上存在
，使得
，则（ ）
A、
B、
C、
或 D、
10、对任意实数
规定
取
三个值中的最小值，则函数（ ）
A、有最大值2，最小值1， B、有最大值2，无最小值，
C、有最大值1，无最小值， D、无最大值，无最小值。
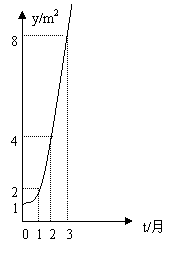11、如图所示的是某池塘中的浮萍蔓延的面积(
)与时间
(月)
的关系:
,有以下叙述:
① 这个指数函数的底数是2;
② 第5个月时,浮萍的面积就会超过
;
③ 浮萍从
蔓延到
需要经过1.5个月;
④ 浮萍每个月增加的面积都相等;
⑤ 若浮萍蔓延到
、
、
所经过的时间
分别为
、
、
，则
.
其中正确的是 ( )
A. ①② B.①②③④ C.②③④⑤ D. ①②⑤
12、函数
在
上是增函数，则实数
的取值范围是（
）
或
第II卷
二、
填空题：（每小题4分，共4小题，合计16分）
13、已知函数
的定义域为
，则函数的定义域为_________。
14、将
这三个数从小到大排列为__________________。
15、已知
，若
，则
。
16、下列几个命题
①方程
的有一个正实根，一个负实根，则。
②函数
是偶函数，但不是奇函数。
③函数
的值域是
，则函数
的值域为
。
④
设函数定义域为R，则函数
与
的图象关于轴对称。
⑤一条曲线
和直线
的公共点个数是
，则的值不可能是1。
其中正确的有___________________。
三、 解答题：（17、18每题6分，19、20每题8分，21、22每题10分，合计48分）
17、已知
，求
的值。
18、计算：（1）已知
求
的值。
（2）
的值。
19、已知函数
，求函数的定义域，并讨论它的奇偶性和单调性。
20、已知函数
的定义域为
，
（1） 求函数的单调区间；
（2） 求函数的值域。
21、定义在非零实数集上的函数满足
，且是区间
上的递增函数。
（1）
求：
的值；
（2）
求证：
；
（3）解不等式
。
22、已知是定义在[-1，1]上的奇函数，当
，且
时有
。
（1）
判断函数的单调性，并给予证明；
（2）
若
对所有
恒成立，求实数m的取值范围。
答案
一、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | D | B | D | B | C | B | C | B | D | B |
二、填空题：
13、
14、
15、－1或2 16、①⑤
三、解答题：
17、解：B={2}
∴方程x2+ax+b=0有两个相等实根为2
∴a=－4,b=4
∴a+b=0
18、解：(1) a+a-2=(a－a-1)2=3
∴原式=0
(2)原式=(lg2+lg5)[(lg2)2－lg2lg5+(lg5)2]+3lg2lg5
=(lg2)2+2lg2lg5+(lg5)2
=(lg2+lg5)2
=1
19、解：(1)定义域为(－1,1)
(2)f(-x)=
=-f(x) ∴函数是奇函数
(3) 在x∈(－1，1)时
y=1－x是减函数
是增函数
是增函数
是增函数
20、解：(1)令t=
，则y=t2－t+1=(t－
)2+
当时x∈[1,2]，t=是减函数，此时t
，y=t2－t+1是减函数
当时x∈[－3,1]，t=是减函数，此时t
，y=t2－t+1是增函数
∴函数的单调增区间为[1,2]，单调减区间为[－3,1]
(2)∵x∈[－3,2]，∴t
∴值域为
21、解：(1)令x=y=1，则f(1)=f(1)+ f(1) ∴f(1)=0
令x=y=－1，则f(1)=f(－1)+ f(－1) ∴f(－1)=0
(2)令y=－1，则f(－x)=f(x)+f(－1)=f(x) ∴f(－x)=f(x)
(3)据题意可知，函数图象大致如下：
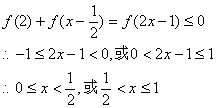
22、(1)证明：令－1≤x1<x2≤1，且a= x1，b=－x2
则
∵x1－ x2<0，f(x)是奇函数 ∴f(x1)－f(x2)<0即f(x1)<f(x2)
∵x1<x2 ∴f(x)是增函数
(2)解：∵f(x)是增函数，且f(x)≤m2－2bm+1对所有x∈[－1,2]恒成立
∴[f(x)]max≤m2－2bm+1 [f(x)]max=f(1)=1
∴m2－2bm+1≥1即m2－2bm≥0在b∈[－1,1]恒成立
∴y= －2mb+m2在b∈[－1,1]恒大于等于0
∴
∴
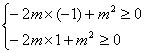
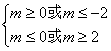
∴m的取值范围是