1．命题“a、b都是偶数，则a+b是偶数”的逆否命题为

A．a+b不是偶数，则a、b不都是偶数B．a+b不是偶数，则a、b都不是偶数

C．a、b不都是偶数，则a+b不是偶数D．a、b都不是偶数，则a+b不是偶数

2．把下列命题改写成“若p则q”的形式：

（1）对顶角相等；　　　　　 （2）不等式两边加上同一个数，不等号方向不变．

3．把下列命题改写成“若p则q”的形式：

（1）两个整数和为整数；　　　　（2）两个无理数相乘，它们的积也是无理数．

4．下列命题中，正确的是

①“若x²+y²=0，则x，y全是0”的否命题　②“全等三角形是相似三角形”的否命题　③“若m＞1，则mx²－2（m+1）x+（m－3）＞0的解集为R”的逆命题　④若“a+5是无理数，则a是无理数”的逆否命题

A．①②③ B．①④　　C．②③④　　 D．①③④

5．用反证法证明：“在同圆中，如果两条弦不等，那么它们的弦心距也不等．”

6．若x、y∈R⁺，且x+y＞2，求证：＜2与＜2中，至少有一个成立．

参考答案

1．A

2．（1）若两角为对顶角，则它们相等；（2）若在不等式两边加上同一个数，则不等式方向不变．

3．（1）若两个数为整数，则它们的和也为整数．（2）若两个无理数相乘，则它们的积也是无理数．

4．B

5．证明：假设在同圆中，两条弦不等而它们的弦心距相等，

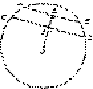
即AB≠CD，OE=OF则Rt△OAE、Rt△OCF中，OA=OC，OE=OF，

∴AE=CF，即AB=CD与已知矛盾，所以假设不成立，原命题成立．

6．证明：假设都不成立，即≥2，≥2成立

∵x，y∈R⁺，∴1+x≥2y，1+y≥2x，∴2+x+y≥2x+2y

∴x+y≤2与已知x+y＞2矛盾，∴假设不成立，∴原结论成立．

一、选择题（每小题2分，共12分）

1．命题“内错角相等，则两直线平行”的否命题为

A．两直线平行，内错角相等B．两直线不平行，则内错角不相等

C．内错角不相等，则两直线不平行D．内错角不相等，则两直线平行

2．已知原命题“菱形的对角线互相垂直”，则它的逆命题、否命题、逆否命题的真假判断正确的是

A．逆命题、否命题、逆否命题都为真B．逆命题为真，否命题、逆否命题为假

C．逆命题为假，否命题、逆否命题为真D．逆命题、否命题为假，逆否命题为真

3．如果一个命题的逆命题为真命题，那么它的否命题

A．一定是真命题B．一定是假命题C．不一定是真命题　　D．真假无法确定

4．命题“正数a的平方不等于0”是命题“若a不是正数，则它的平方等于0”的

A．逆命题 B．否命题　　　C．逆否命题　　　 D．否定命题

5．命题“若M∪N=N，则MN”的否命题为

A．若MN，则M∪N=N　 　　 B．若M∪N≠N，则MN

C．若MN，则M∪N≠N　　　　D．若M∩N=M，则M∪N=N

6．命题“若a>b，则>1”的逆否命题为

A．若>1，则a>b　　B．若a≤b，则≤1　C．若a>b，则b<a　　D．若≤1，则a≤b

二、填空题（每小题2分，共8分）

7．命题“垂直于同一直线的两条直线相互平行”的逆命题为______________．

8．命题“若a>1，则a>0”的否命题为_____________．

9．命题“全等三角形的面积相等”的逆否命题为________________．

10．给出下列命题：

①命题“若b²－4ac<0，则方程ax²+bx+c=0（a≠0）无实根”的否命题

②命题“△ABC中，AB=BC=CA，那么△ABC为等边三角形”的逆命题

③命题“若a>b>0，则>>0”的逆否命题；其中真命题的序号为__________．

三、解答题（共30分）

11．（10分）把下列命题改写成“若p则q”的形式：

（1）菱形的四边相等； （2）对顶角相等；（3）25是5的倍数；　（4）是无理数．

12．（10分）试判断命题“若m>0，则方程x²+x－m=0有实根”的逆否命题的真假．

13．（10分）用反证法证明：若x²－（m+n）x+mn≠0，则x≠m且x≠n．

参考答案

一、1．C　2．D　3．A　4．B　5．B　6．D

二、7．两条直线互相平行则它们垂直于同一条直线　8．若a≤1，则a≤0　

9．面积不相等的两个三角形不是全等三角形　10．①②③

三、11．（1）若四边形为菱形，则其四边相等（2）若两个角是对顶角，则它们相等

（3）若某数为25，则它为5的倍数（4）若一个数为，则它为无理数

12．真

13．证明：假设x=m或x=n

（1）当x=m时，则x²－（m+n）x+mn=0（2）当x=n时，则x²－（m+n）x+mn=0均与已知矛盾，∴x≠m且x≠n．

一、选择题

1．一个命题与它的逆命题、否命题、逆否命题这四个命题中（　）

A.真命题的个数一定是奇数　　　　　　　　　 B.真命题的个数一定是偶数

C.真命题的个数可能是奇数也可能是偶数　　　 D.上述判断都不正确

二、填空题

2．命题“若x=3且y=5则x+y=8”的逆否命题是________，否命题是________，逆命题是_________，其中假命题的个数是____________。

3．命题“各位数字之和是3的倍数的正整数，可以被3整除”的逆否命题是___________；逆命题是__________；否命题是_____________。

三、解答题

4．用反证法证明：若且x∈R，y∈R，则x、y全为0。

5．若a、b、c均为实数，且，，，

求证：a、b、c中至少有一个大于0。

6．利用反证法证明

已知a、b、c∈R，a+b+c>0，ab+bc+ac>0，abc>0，求证a>0，b>0，c>0。

7．分别写出下列命题的逆命题，否命题，逆否命题，并判断真假。

（1）若q<1，则方程有实根；

（2）若ab=0，则a=0或b=0。

8．证明：若△ABC不是正三角形，则内角A、B、C中必有一个大于60°。

参考答案

1．B　∵一个命题与它的逆否命题同真同假，一个命题的逆命题与它的否命题是同真同假，

∴真命题的个数一定是偶数。故选B。

2．若x+y≠8则x≠3或y≠5；若x≠3或y≠5，则x+y≠8；若x+y=8则x=3且y=5；2

3．原命题的逆否命题：不能被3整除的正整数，其各位数字之和不是3的倍数；逆命题是：能被3整除的正整数，它的各位数字之和是3的倍数；否命题是：各位数字之和不是3的倍数的正整数，不能被3整除。

4．证明：假设x、y不全为0，则x≠0或者y≠0。

由x≠0得到，而，，，矛盾

所以x=0

由，而，，，矛盾

所以y=0

5．证明：假设a、b、c都不大于0，即a≤0，b≤0，c≤0，则有a+b+c≤0，而

。

因为π-3>0且无论x，y，z为何实数，。

所以a+b+c>0，这与a+b+c≤0矛盾，因此假设不成立，a，b，c中至少有一个不大于0。

6．证明：假设a、b、c不同时为正，不妨先考虑a不是正数，从而有a=0和a<0两种情况。

若a=0，则abc=0，与已知abc>0矛盾，故a=0不可能。若a<0，因为abc>0，所以bc<0，又因为a+b+c>0，所以b+c>-a>0。所以ab+bc+ac=a（b+c）+bc<0。这与已知ab+bc+ac>0矛盾，所以a<0也不可能。

综上所述a>0成立。同理可知b>0、c>0成立。原命题得证。

7．解：（1）逆命题：若方程有实根，则q<1，逆命题为假。

否命题：若q≥1，则方程无实根，否命题为假。

逆否命题：若方程无实根，则q≥1，逆否命题为真。

（2）逆命题：若a=0或b=0，则ab=0，逆命题为真。

否命题：若ab≠0，则a≠0且b≠0，否命题为真。

逆否命题：若a≠0，且b≠0，则ab≠0，逆否命题为真。

8．证明：假∠A≤60°，∠B≤60°，∠C≤60°，则∠A+∠B+∠C=180°，因为∠A+∠B+∠C≤180°，所以∠A=∠B=∠C=60°，所以△ABC为正三角形，这与△ABC不是正三角形矛盾，故假设错误。所以命题成立。

一、选择题

1．命题“若a∈A，则”的否命题是(　　)

A．若，则　　　　　　　　　　　　　　　　　　　　 B．若，则

C．若，则b∈B　　　　　　　　　　　　　　　　　　　　　 D．若b∈B，则

2．若一个命题的否命题是真命题，则其逆命题(　　)

A．不一定是真命题B．一定是真命题C．一定是假命题　　　D．不一定是假命题

3．命题“若ab＝0，则a＝0或b＝0”的逆否命题是(　  )

A．若a＝0或0　　　　　　　　　　　　　　　 B．若ab≠0，则a≠0且b≠0

C．若ab＝0，则a≠0且b≠0　　　　　　　　　　　　　　　　D．若a≠0且b≠0，则ab≠0

4．命题“若a>b，则ac>bc”(a，b，c都是实数)与其逆命题、否命题、逆否命题中真命题的个数为(　　)

A．4　　 B．2　　　　C．3　　　　　　　　　　　D．0

5．给出以下四个命题：

(1)若，则x＝2或x＝3；(2)若2≤x<3，则(x－2)(x－3) ≤0；

(3)若a＝b＝0，则a＋b＝0；(4)若x，y∈N，x＋y是奇数，则x，y中一个是奇数，一个是偶数．那么(　　)

A．(4)的逆命题假B．(1)的逆命题真C．(2)的否命题真　　　　D．(3)的否命题假

二、填空题

1．命题“若ab>0，则a>0且b>0”的逆命题是_________，否命题是________，逆否命题是________．

2．命题“若x、y是奇数，则x＋y是偶数”的逆否命题是_________________．

3．命题“若a≠0，则ab≠0”与它的逆命题、否命题、逆否命题中，真命题的个数为_________________．

三、解答题

1．指出命题：“内接于圆的四边形的对角互补”及其否命题、逆命题、逆否命题中哪些是真命题，哪些是假命题．

2．a、b、c为实数，且a＝b＋c＋1，证明：两个一元二次方程，中至少有一个方程有两个不相等的实数根．

四、问答题

1．若命题p的逆命题是q，命题p的否命题是r，则q是r的_________________．

2．求证．

参考答案

【同步达纲练习】

一、1．C　 2．B　 3．D　 4．D提示：∵原命题不成立(令c＝－2，a＝3，b＝2，则)　　5．B

二、1．若a>0且b>0，则ab>0;若ab≤0，则a≤0或b≤0;若a≤0或b≤0，则ab≤0

2．若x＋y不是偶数，则x，y不都是奇数

3．2　但

三、1．否命题：“若一个四边形不内接于圆，则它的对角不互补”．

逆命题：“若一个四边形的对角互补，则它内接于圆”．

逆否命题：“若一个四边形的对角不互补则它不内接于圆”．

都是真命题

2．反证法：设两个方程都没有两个不等的实数根

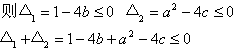
∵a＝b＋c＋1，∴b＋c＝a－1∴

即但，故矛盾！

四、1．逆否命题：

提示：设p：若A则B，则q：若B则A，r：若则，则r与q关系显然

2．反证法：

证明：假设则存在x，使得

∴x∈A且　这是矛盾关系！∴

一、选择题.

1.命题“当AB=AC时，△ABC是等腰三角形”与它的逆命题、否命题、逆否命题这四个命题中，真命题的个数是(　　)

A.4　　　　  B.3　　　　  C.2　　　　   D.0

2.若命题p的逆命题是q，命题q的否命题是r，则r是p的(　　)

A.逆命题　　　B.否命题　　　C.逆否命题　　　　 D.以上判断都不正确

3.如果一个命题的否命题是真命题，那么这个命题的逆命题是(　　)

A.真命题 　　 B.假命题　　  C.不一定是真命题　　　 D.不一定是假命题

4.设原命题为“若A∩B=B，则AB”，则原命题、逆命题、否命题和逆否命题中是真命题的个数是(　　)

A.0个　　　　　　 B.1个　　　　　　 C.2个　　　　　　 D.4个

5.在下列三个命题中，正确的为(　　)

(1)命题“△ABC和△A₁B₁C₁都是直角三角形”的否命题是“△ABC和△A₁B₁C₁都不是直角三角形”；

(2)命题“若xy≠0，则x≠0且y≠0”的逆否命题是“若x＝0或y＝0，则xy=0”；

(3)命题“若x∈A或x∈B，则x∈A∪B”的逆命题是“若x∈A∪B，则x∈A且x∈B”.

A.(2)　　　　　　　B.(2)、(3)　　　　 C.(1)、(3)　　　　 D.(1)、(2)、(3)

6.在以下四个命题中，不正确的为(　　)

A.命题“两个无理数的积仍是无理数”的逆命题是“乘积为无理数的两数都是无理数”；

B.命题“两个无理数的积仍是无理数”的否命题是“两个不都是无理数的积也不是无理数”；

C.命题“两个无理数的积仍是无理数”的逆否命题是“乘积不是无理数的两个数都不是无理数”；

D.命题“两个无理数的积仍是无理数”的命题的非是“两个无理数的积不一定是无理数”.

二、填空题

1.命题“若x²+y²=0，则x、y全为0”的否命题是　　　　　 .

2.命题“若a、b是奇数，则a+b是偶数”的逆否命题是　　　　　 .

3.命题“已知a，b，c，d∈R，若a=b，c=d，则a+c=b+d”的逆命题为　　　　　 ；否命题为　　　　　 .

4.命题“正数的绝对值等于它本身”的逆命题是　　　　　 .

三、解答题

1.把下列命题写成“若p则q”的形式

①到圆心距离等于半径的点在圆上　　 ②三角形内角和等于180°

③两个有理数的商仍为有理数　　　　 ④实数的平方为正实数

2.写出下列命题的逆命题，否命题，逆否命题，并判断这些命题的真假.

①实数的平方为正实数　　 ②三角形的两边之和不小于第三边

③若a＞b，则b＜a　　　　④若m，n∈Q，则m+n∈Q

3.用反证法证明：若a＞b＞0，则＞.

4.用反证法证明：如果一个三角形的两条边不等，那么这两条边所对的角也不相等.

5.用反证法证明：圆的两条不是直径的相交弦不能互相平分.

四、1.a、b、c∈R，写出命题“若ac＜0，则ax²+bx+c=0有两个不相等实根”的逆命题、否命题、逆否命题的真假.

2.证明：在△ABC中，若AB=AC，M为△ABC内一点，∠AMB＞∠AMC，则∠BAM＜∠CAM.

参考答案：

一、1.C　2.C　3.A  4.A　5.A　6.C

二、1.“若x²+y²≠0，则x、y不全为0”.　　2.若a+b不是偶数，则a、b不都是奇数.　　3.逆命题为：已知a、b、c、d∈R，若a+c=b+d，则a=b，c=d.　否命题为：已知a、b、c、d∈R，若a≠b或c≠d，则a+c≠b+d.　　4.绝对值等于它本身的数是正数.

三、1.解：①若点到圆心的距离等于半径，则该点在圆上.②若一个图形是三角形，则它的内角和等于180°.

③若两个数是有理数，则它们的商仍为有理数.④若一个数是实数，则它的平方是一个正实数.

2.①原命题：若一个数是实数，则它的平方是一个正实数，为假，因为0的平方就不是正实数.

逆命题：若一个数的平方为正实数，则这个数是实数，为真.

否命题：若一个数不是实数，则它的平方也不是一个正实数，为真.

逆否命题：若一个数的平方不是正实数，则它不是实数.为假

②原命题：若一个图形是三角形，则它的两边之和不小于第三边.为真

逆命题：若两条线段的长的和不小于第三条线段的长，则以这三条线段构成一个三角形.为假

否命题：若三条线段不参构成三角形，则其中两条线段长的和小于第三条线段的长.为假

逆否命题：若两条线段的长的和小于第三条线段的长，则这三条线段构不成一个三角形.为真

③原命题：若a＞b，则b＜a，为真　　 逆命题：若b＜a，则a＞b，为真

否命题：若a≤b，则b≥a，为真　　　 逆否命题：若b≥a，则a≤b，为真

④原命题：若m，n∈Q，则m+n∈Q，为真

逆命题：若m+n∈Q，则m，n∈Q为假，如(3+)+(5-)∈Q，但3+Q，5-Q

否命题：若mQ或nQ，则m+nQ为假　　　逆否命题：若m+nQ，则mQ或nQ为真

3.略　　4.略　　5.略.

四、1.解：原命题是真命题，这是因为方程的判别式△=b²-4ac，b²≥0，-4ac＞0，所以△＞0.

逆命题：“若ax²+bx+c=0(a、b、c∈R)有两个不相等的实根，则ac＜0”，它是假命题.如当a=1，b=-3，c=2时，方程x²-3x+2=0有两个不相等的实根x₁=1，x₂=2，但ac=2＞0.

否命题：“若ac≥0，则方程ax²+bx+c=0(a、b、c∈R)没有两个不相等的实数”，它也是假命题.这是因为它和逆命题互为逆否命题，而逆命题是假命题的缘故.

逆否命题：“若ax²+bx+c=0(a、b、c∈R)没有两个不相等的实数根，则ac≥0”，它是真命题.

2.提示：假设∠BAM≥∠CAM，然后分二种情况(即∠BAM＞CAM和∠BAM=∠CAM)推出矛盾结果.

三、参考练习题

1．在下列命题中，真命题是（　　）

①“在同一个三角形中，大边对大角”的否命题．②“若m≤1，则x²－2x＋m＝0有实根”的逆命题．

③“菱形的对角线互相垂直平分”的否命题．④“若A∩B＝B，则AB”的等价命题．

A．①②④　　　　　　　　　 B．③④　　　　　　 C．①②　　　　　　　　　 D．①②③

答案：D

2．命题“若a＞b，则am＞bm”与它的逆命题、否命题，逆否命题中真命题共有____个．答案：0

3．写出命题“对角线不互相垂直的平行四边形不是菱形．”的逆命题、否命题、逆否命题，并指出它们的真假．

答案：逆命题为：“不是菱形的平行四边形，对角线不互相垂直”，为真命题．

否命题为“对角线互相垂直的平行四边形是菱形”，为真命题．

逆否命题为“平行四边形是菱形，其对角线互相垂直”，为真命题．

4．判断下列命题的否命题的真假．

（1）正方形四条边相等．（2）已知a＜0，如果x＝－a，那么x＜0（3）一个锐角的补角是钝角．

答案：（1）否命题为假命题．　（2）否命题为假命题．　（3）否命题为真命题．

1．命题“若aA，则b∈B．”的否命题是

A．若aA，则bB 　B．若a∈A，则bB　 C．若b∈B，则aA 　 D．若bB，则aA

2．命题“正数不是质数”与它的逆命题、否命题、逆否命题这四个命题中，假命题有___________个

A．4 B．3　　C．2　D．0

3．有下列四个命题，其中为真命题的是

①“若xy＝1，则x，y互为倒数”的逆命题；②“面积相等的三角形全等”的否命题；

③“若m≤1，则x²－2x＋m＝0有实根”的逆否命题；④“若A∩B＝B，则AB”的逆否命题．

A．①②　　　　B．②③　　　 C．①②③　　 D．③④

4．命题“若A∩B＝A，则A∪B＝B”的逆否命题是

A．若A∪B＝B，则A∩B＝A　　　　B．若A∩B≠A，则A∪B≠B

C．若A∪B≠B，则A∩B≠A　　　　D．若A∪B≠B，则A∩B＝A

5．命题“x或y是零，则xy是零”的逆否命题是_________．

6．已知m，n是正整数，a是大于1的实数，“若m＞n，则a^m＞aⁿ”的逆否命题是_________．

7．命题“若a＞b，则ac＞bc”与它的逆命题、否命题、逆否命题中，有_________个真命题．

8．命题：“已知a，b，c，d是实数，若a＝b，c＝d，则a＋c＝b＋d”写出该命题的逆命题、否命题、逆否命题，并判断其真假．

9．判断命题“若x≤－3，则x²－x－6＞0”的否命题的真假．

参考答案

一、1．B　提示：注意“∈”的否定是“”．

2．A　提示：因为“正偶数不是质数”是假命题，所以其逆否命题也为假，又因其否命题“正偶数是质数”是假命题，所以其否命题也为假．

3．C　提示：④若A∩B＝B，应用BA．

4．C　提示：注意“A∩B＝A”的否定是“A∩B≠A”．

二、5．“x或y是零，则xy是零”的逆否命题是“若xy不是零，则x，y都不是零”．

6．填：已知m，n是正整数，a是大于1的实数，“若a^m≤aⁿ，则m≤n”．

7．0　提示：因为a＞b，c＝0时，ac＝bc，所以原命题为假，又因若“ac＞bc则a＞b”是假命题，所以4个命题均为假命题．

三、8．解：逆命题：“已知a，b，c，d是实数，若a＋c＝b＋d，则a＝b，c＝d．”是假命题．

否命题：“已知a，b，c，d是实数，若a与b，c与d不都相等，则a＋c≠b＋d”．(假命题)

逆否命题：“已知a，b，c，d是实数，若a＋c≠b＋d，则a与b，c与d不都相等”是真命题．

9．解：该命题的否命题为：“若x＞－3，则x²－x－6≤0”．

p:A＝｛x｜x＞－3｝．q:B＝｛x｜x²－x－6≤0｝＝｛x｜－2≤x≤3｝

∵BA，∴若p则q为假．∴该命题的否命题为假命题．

1．命题“两条对角线相等的四边形是矩形”是命题“矩形是两条对角线相等的四边形”的(　　)

A．逆命题　　B．否命题　　 C．逆否命题　　  D．无关命题

解析： 依逆命题定义易得．

答案： A

2．命题“对顶角相等”与它的逆命题、否命题、逆否命题中，真命题是(　　)

A．上述四个命题　　　　　　　　　　　  B．原命题与逆命题

C．原命题与逆否命题　　　　　　　　　  D．逆命题与否命题

解析： 因真命题“对顶角相等”的逆命题“相等的角是对顶角”是假命题．

答案： C

3．用反证法证明命题“＋是无理数”时，假设正确的是(　　)

A．假设是有理数　　　　　　　 B．假设是有理数

C．假设或是有理数　　　　  D．假设＋是有理数

答案： D

4．命题“若A∪B＝A，则A∩B＝B”的否命题是(　　)

A．若A∪B≠A，则A∩B≠B　 B．若A∩B＝B，则A∪B＝A

C．若A∩B≠B，则A∪B≠A　 D．若A∪B≠A，则A∩B＝B

答案： A

5．命题“若a＞1，则a＞0”的逆命题是______，逆否命题是______．

答案： 若a＞0，则a＞1  若a≤0，则a≤1

6．给定下列命题：

①“若k＞0，则方程x²＋2x－k＝0”有实数根；②“若a＞b，则a＋c＞b＋c”的否命题；

③“矩形的对角线相等”的逆命题；④“若xy＝0，则x、y中至少有一个为0”的否命题．

其中真命题的序号是______．

解析： ①Δ＝4－4(－k)＝4＋4k＞0∴是真命题

②否命题为“若a≤b，则a＋b≤b＋b”是真命题

③逆命题“对角线相等的四边形是矩形”是假命题

④否命题：“若xy≠0，则x、y都不为零”是真命题

答案： ①②④

1．若命题p的否命题为r，命题r的逆命题为s，则s是p的逆命题t的(　　)

A．逆否命题　　  B．逆命题　　　　 C．否命题　　　　　  D．原命题

解析： 设p为“若A则B”，则r、s、t分别为“若﹁A则﹁B”“若﹁B则﹁A”“若B则A”，故s是t的否命题．

答案： C

2．当命题“若p则q”为真时，下列命题中一定正确的是(　　)

A．若q则p　　　　  B．若﹁q﹁p　　 C．若﹁q则﹁p　　　　D．p且q

解析： 因原命题与逆否命题等价，故选C．

答案： C

3．一个命题与它的逆命题、否命题、逆否命题这四个命题中(　　)

A．真命题的个数一定是奇数　　　　　　　　　　 B．真命题的个数一定是偶数

C．真命题的个数可能是奇数也可能是偶数　　　　 D．上述判断都不正确

解析： 因“原命题”与“逆否命题”同真假，“逆命题”与“否命题”同真假，故真命题是成对出现的．

答案： B

4．有下列四个命题，其中真命题是(　　)

①“若xy＝1，则x，y互为倒数”的逆命题；②“相似三角形的周长相等”的否命题；

③“若b≤－1，则方程x²－2bx＋b²＋b＝0有实根”的逆否命题；④“若A∪B＝B，则AB”的逆否命题．

A．①②　 B．②③　 C．①③　 D．②④

答案： C

5．命题“若A∪B＝B，则AB”的否命题是______，逆否命题是______．

答案： 若A∪B≠B，则AB　若AB，则A∪B≠B

6．用反证法证明命题“若整数n的立方是偶数，则n也是偶数”如下：

假设n是奇数，则n＝2k＋1(k是整数)，n³＝(2k＋1)³＝______，与已知n³是偶数矛盾，所以n是偶数．

解析： (2k＋1)³＝8k³＋12k²＋6k＋1＝2(4k³＋6k²＋3k)＋1

答案： 2(4k³＋6k²＋3k)＋1

7．把下列命题写成“若p则q”的形式，并写出它们的逆命题、否命题与逆否命题．

(1)当x＝2时，x²－3x＋2＝0；(2)对顶角相等．

解：(1)原命题：若x＝2，则x²－3x＋2＝0

逆命题：若x²－3x＋2＝0，则x＝2

否命题：若x≠2，则x²－3x＋2≠0

逆否命题：若x²－3x＋2≠0，则x≠2

(2)原命题：若两个角是对顶角，则它们相等．

逆命题：若两个角相等，则它们是对顶角．

否命题：若两个角不是对顶角，则它们不相等．

逆否命题：若两个角不相等，则它们不是对顶角．

8．命题：“已知a，b，c，d是实数，若a＝b，c＝d，则a＋c＝b＋d”．写出该命题的逆命题、否命题、逆否命题，并判断这些命题的真假．

解：逆命题：“已知a，b，c，d是实数，若a＋c＝b＋d，则a＝b，c＝d(即a与b、c与d都相等)．”

否命题：“已知a、b、c、d是实数，若a与b、b与d不都相等，则a＋b≠b＋d”．

逆否命题：“已知a，b，c，d是实数，若a＋c≠b＋d，则a与b、c与d不都相等．”

原命题是真命题．

若令a＝3，b＝2，c＝1，d＝2，则a＋c＝1＋3＝4，b＋d＝2＋2＝4，即a＋c＝b＋d．但a≠b，c≠d，所以逆命题为假命题．

根据原命题与逆否命题、逆命题与否命题等价的性质．所以逆否命题为真命题，否命题为假命题．

9．已知a、b、c是一组勾股数(即a²＋b²＝c²)，求证：a、b、c不可能都是奇数．

证明：假设a、b、c都是奇数∵a、b、c是一组勾股数，∴a²＋b²＝c²①

∵a、b、c都是奇数，∴a²、b²、c²也都是奇数∴a²＋b²是偶数

这样①式的左边是偶数，右边却是奇数，得出自相矛盾的结论．

∴a、b、b不可能都是奇数．

10．已知m、n为实数，命题“若mn＝0，则m＝0或n＝0”的否命题、逆否命题各是什么?命题“若m²＋n²＝0，则m＝0且n＝0”的否命题、逆否命题各是什么?并判断以上各命题的真假．

解：“若mn＝0，则m＝0或n＝0”的否命题是“若mn≠0，则m≠0且n≠0”．逆否命题是“若m≠0且n≠0，则mn≠0”．

命题“若m²＋n²＝0，则m＝0且n＝0”的否命题是“若m²＋n²≠0，则m≠0或n≠0”；逆否命题是“若m≠0或n≠0，则m²＋n²≠0”．

以上各命题都是真命题．

1．若p，q是两个简单命题，且“p或q”的否定是真命题，则必有

A．p真q真　　B．p假q假　　　　 C．p真q假　　　 D．p假q真

2．关于实数a，b，c以下叙述错误的是

A．命题“a，b都是零”的否定形式是“a，b都不是零”

B．命题“a，b至少有一个是零”的否定形式是“a，b都不是零”

C．命题“a，b，c至多两个是零”的否定形式是“a，b，c都是零”

D．命题“a，b，c至少两个是零”的否定形式是“a，b，c至多一个是零”

3．否定结论“至多有两个解”的记法中，正确的是

A．有一解　　　B．有两解　　　　C．至少有三解　 　D．至少有两解

4．用反证法证明命题“已知△A′BC与△ABC有公共边BC，且∠BA′C＜∠BAC，求证A′在△ABC的外部”时，反设正确的是

A．设点A′在△ABC的外部　　　　  B．设点A′在△ABC的边上

C．设点A′在△ABC的内部　　　　  D．设点A′在△ABC的边上或在△ABC的内部

5．若0＜x＜5，则｜x－2｜＜5的逆否命题是_________．

6．x≠±1的否定形式为_________，(x－1)(x－2)＝0的否定形式为___________．

7．用反证法证明命题“若a∈R，3＋a是无理数，则a是无理数”如下：假设a是有理数，根据有理数运算法则，3＋a是有理数，这与_________矛盾，所以假设不成立，原命题正确．

8．已知a，b是实数，命题“若a²＋b²＝0，则a＝0且b＝0”的否命题，逆否命题各是什么？

参考答案

一、1．A　提示：“或”的否定是“且”．

2．A　提示：“都是”的否定是“不都是”而不是“都不是”．

3．C　提示：“至多有n个”的否定是“至少有n＋1个”．

4．D　提示：“外部”的反面是“内部或边上”．

二、5．填“若｜x－2｜≥5，则x≥5或x≤0”．

6．x≠±1的否定形式为x＝1或x＝－1

(x－1)(x－2)＝0的否定：x－1≠0且x－2≠0．

7．与“3＋a是无理数”矛盾．

三、8．解：命题a²＋b²＝0，则a＝0且b＝0的否命题是：若a²＋b²≠0，则a≠0或b≠0．

逆否命题是：若a≠0或b≠0，则a²＋b²≠0