高一数学第二学期期末质量抽测试卷

一、填空题（本大题共10小题，每小题3分，满分30分）

1．计算：　　　　　　 .

2．函数的反函数　　　　　　　　 .

3．若函数在上是减函数，则的取值范围是　　　　　 　　 .

4．若点是角终边上的一点,则　　　　　　　 .

5．在半径为2的圆中，弧长为1的圆弧所对的圆心角的弧度数为　　　　　　　　 .

6．已知，化简：　　　　　　　　  .

7．在中，设分别是三个内角所对的边，且，　　.

8．函数，的值域是　　　　　　　 .

9．在中，设分别是三个内角所对的边，，面积，

则内角的大小为　　　　　　　  .

10．方程及在区间的根分别为，则

的大小关系为　　　　　　  .

二、选择题（本大题共6小题，每小题3分，满分18分）

11．方程的解是……………………………………………………（　　）

A．　　　　　　　　　　　　　B．　　　　　　　　　　　　　 C．　　　　　　　　 D．

12．在中,“”是“”的……………………………………（　　）

A. 充分不必要条件　　　　　　　　　　　　　　　　　　　　 B. 必要不充分条件　

C. 充要条件　　　　　　　　　　  　　　　　　 D. 既不充分也不必要条件

13．函数的单调递减区间是……………………………………………………（　　）

A．　　　　 　　　B．

C．　　　　　  D．

14．今有一组实验数据如下：

	1.95	3.00	3.94	5.10	6.12
	0.97	1.59	1.98	2.35	2.61

　　　　　　　　　　　　　　　　　　　　　 　 

现准备用下列函数中的一个近似地表示这些数据满足的规律，其中最合适

的一个是…………………………………………………………………………………（　　）

A．　　　　　　　　　B．　　　　　　　C．　　　　D．

15．函数的图像无论经过平移或沿直线翻折后仍不能与的图像重合，

则可以是……………………………………………………………………………（　　）

A．　　　　　　　B．　　　　C．　　 D．

16．已知函数的图像是下列两个图像中的一个，请你选择后再根据图像

作出下面的判断：若且，则…………………………（　　）

A． B．　　　　　　C． D．

三、解答题（本大题共5小题，满分52分）

17．（本小题满分8分）

已知函数

（1）求的最小正周期；

（2）求的最大值和最小值.

18．（本小题满分8分）

已知.

（1）求的值；

（2）求的值.

19．（本小题满分10分）

设函数，（为常数且）

（1）若，求的解析式；

（2）在（1）的条件下，解方程：.

20．（本小题满分12分）

如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营

救．甲船立即前往，同时把消息告知在A处的南偏西30，相距10海里C处的乙船，试

问乙船应朝北偏东多少度的方向沿直线前往B处救援（角度精确到1）？

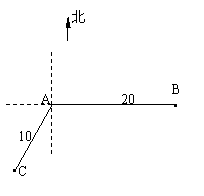21．（本小题满分14分）

已知函数的图像关于直线对称，当时，

函数（）的图像如图所示；

（1）求常数、的值；

（2）求函数在上的解析式；

（3）求方程的解集。

浦东新区2006学年度第二学期期终考试

高一年级数学试卷参考解答及评分说明

说明：

1.本解答列出试题的一种解法，如果学生的解法与所列解法不同，可参照解答中评分标准进行评分。

2.评阅试卷，应坚持每题评阅到底，不要因为学生的解答中出现错误而中断对该题的评阅。当学生的解答在某一步出现错误，影响了后继部分，但该步以后的解答未改变这一题的难度时，可视影响程度决定后面部分的给分，这时原则上不应超过后面部分应给分数之半，如有较严重的概念性错误，就不给分。

3.第17题至第21题中右端所注的分数，表示学生正确做到这一步应得的该题的累加分数。

4.给分或扣分均以1分为单位。

一．本题共30分，每小题正确的给3分，否则一律得0分。

1. 4.　 　　　 2. （）.　　　　　3. .　　　　 4. .　 　 5. .　　

6. .　　　7. .　　　8. .　　　　 9. 或.　　　 10. .　 　

二．本题共18分，每小题正确的给3分，否则一律得0分。

11. .　 　　 12. .　　　 13. .　 　  14. .　　 　 15. .　　　　  16. .

三．本题共52分。

17. 本题满分8分　　　　　　　　　　　　 

[解]……………………………………………2分

（1）由，所以函数的最小正周期为；…………………4分

（2）当时，取得最小值；…………………………………6分

当时，取得最大值。…………………………………………8分

18. 本题满分8分　　　　　　　　　　　　　

[解] （1）；…………………………………………………………………3分

（2）显然，…………………………………………………………………………4分

所以

…………………………6分

当时；……………………………………………………………7分

当时；……………………………………………………………8分

19. 本题满分10分

[解] （1）由题设得，所以；…………………………4分

（2）由（1）得（）……………………………………………6分

于是方程或……………………9分

经检验或都是原方程的根。……………………………………………………10分

20. 本题满分12分

[解] 连接，设

由题设知……………………………2分

于是,

且，…………………………4分

在中，由正弦定理得

…7分

……10分

，乙船应朝北偏东的方向沿直线前往B处救援………………………………12分

21. 本题满分14分

[解] （1）、；………………………………4分

（2）当时，

函数

当时，，

， …………8分

综上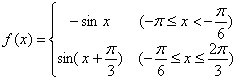 ………………………………………………10分

（3）的解集为。………………………………………14分