高一新课程质量检测数学试题(2008.7)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分120分.测试时间120分钟.
第Ⅰ卷(选择题共 48分)
注意事项:
1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂在答题卡上.
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选择其它答案标号.不能答在试题卷上.
3. 可使用不含有存储功能的计算器.
一、选择题:本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.
1. 下列框图符号中,表示处理框的是

2.
-![]() 是
是
A. 第一象限的角 B. 第二象限的角 C. 第三象限的角 D. 第四象限的角
3. 某质量监督局要对某厂6月份生产的三种型号的轿车进行抽检,已知6月份该厂共生产甲种轿车1 400辆,乙种轿车6 000辆,丙种轿车2 000辆,现采用分层抽样的方法抽取47辆进行检验,则这三种型号的轿车依次应抽取
A. 14辆,21辆,12辆 B. 7辆,30辆,10辆
C. 10辆,20辆,17辆 D. 8辆,21辆,18辆
4. 将一副54张扑克的扑克牌均匀洗好后,任取其中一张,那么取到“大王”或“小王”的概率为
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
5. 已知角α的终边上有一点(3cos60°,sin60°),则α等于
A. k·180°-30°,k∈Z B. k·180°+30°,k∈Z
C. k·360°-30°,k∈Z D. k·360°+30°,k∈Z
6. 已知向量a=(1,2),b=(x,1),且a+2b与2a-b平行,则x等于
A. 4
B. 2
C. ![]() D.
-
D.
-![]()
7. 函数y=13sin2xcos2x的最小值和周期分别为
A. -![]() ,
,![]() B. -
B. -![]() ,
,![]() C.
C.![]() ,2π D.
,2π D.![]() ,4π
,4π
8. 函数y=sinx的图像是由函数y=3sin(x-![]() )的图像怎样变化而成
)的图像怎样变化而成
A.把图像上所有点向右平行移动![]() 个单位,再把纵坐标伸长到原来的3倍(横坐标不变)
个单位,再把纵坐标伸长到原来的3倍(横坐标不变)
B. 把图像上所有点向左平行移动![]() 个单位,再把纵坐标伸长到原来的3倍(横坐标不变)
个单位,再把纵坐标伸长到原来的3倍(横坐标不变)
C. 把图像上所有点向右平行移动![]() 个单位,再把纵坐标缩短到原来的
个单位,再把纵坐标缩短到原来的![]() 倍(横坐标不变)
倍(横坐标不变)
D. 把图像上所有点向左平行移动![]() 个单位,再把纵坐标缩短到原来的
个单位,再把纵坐标缩短到原来的![]() 倍(横坐标不变)
倍(横坐标不变)
9. 为培育更好的花卉品种,从某一品种花卉在甲、乙两种栽培情况下各取5株,分别测得他们的株高如下:(单位:cm)
甲:25,41,40,37,22
乙:27,16,44,27,46
则此花卉长得高的栽培方式是
A. 甲种 B. 乙种 C. 一样高 D. 无法区别
10. 若tan(β-![]() )=
)=![]() ,则tanβ等于
,则tanβ等于
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11. 函数y=2cos2(![]() -
-![]() ),(x∈ [0,2π])的递减区间是
),(x∈ [0,2π])的递减区间是
A. [0,π] B. [![]() ,π]
C. [
,π]
C. [![]() ,
,![]() ]
D. [
]
D. [![]() ,
,![]() ]
]
12.
点P是△ABC所在平面内的一点,且满足![]() ,则△PAC的面积与△ABC的面积之比为
,则△PAC的面积与△ABC的面积之比为
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
 绝密★启用前
绝密★启用前
济南市高一新课程质量检测(2008.7)数 学 试 题
数 学 试 题
第Ⅱ卷(非选择题 共72分)
注意事项:
1. 用钢笔或圆珠笔直接答在试题卷中.
| 得 分 | 评卷人 |
2. 答题前将密封线内的项目填写清楚.
 二、
填空题:本大题共4个小题,每小题4分;共16分.将答案填在题中横线上.
二、
填空题:本大题共4个小题,每小题4分;共16分.将答案填在题中横线上.
13. 计算sin(-![]() )+cos
)+cos![]() +tan(-
+tan(-![]() )=
.
)=
.
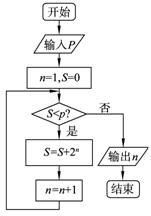
14. 执行右边的程序框图,若p=15,则输出的n= .
15. 已知向量a,b,x满足a=(2,2),b=(1,3),3(a+2x)-2(x-b)=0,
则x= (用坐标表示).
16. arccos![]() +arctan
+arctan![]() =
.
=
.
三、 解答题:本大题共6个小题,共56分.解答应写出文字说明,证明
过程或演算步骤.
| 得 分 | 评卷人 |
17. (本小题满分8分)
已知α是第二象限角,按要求做下列各题:
(1) 已知cosα=-![]() ,求sinα和tanα的值;
,求sinα和tanα的值;
(2) 化简:![]() ·tanα.
·tanα.
18. (本小题满分8分)
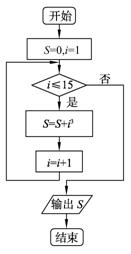
画出求13+23+33+……+153的算法的程序框图.
19. (本小题满分8分)
某外语学校英语班有A1,A2两位同学、日语班有B1,B2,B3,B4四位同学、俄语班有C1,C2两位同学共8人报名奥运会志愿者,现从中选出懂英语、日语、俄语的志愿者各1人,组成一个小组.
(1) 写出一切可能的结果组成的基本事件空间并求出B4被选中的概率;
(2) 求A1和C1不全被选中的概率.
20. (本小题满分10分)
假设关于某设备的使用年限x和所支出的维修费用y(万元)统计数据如下:
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若有数据知y对x呈线性相关关系.求:
(1) 填出右图表并求出线性回归方程
| 序号 | x | y | xy | x2 |
| 1 | 2 | 2.2 | ||
| 2 | 3 | 3.8 | ||
| 3 | 4 | 5.5 | ||
| 4 | 5 | 6.5 | ||
| 5 | 6 | 7.0 | ||
| ∑ |
![]() =bx+a的回归系数
=bx+a的回归系数![]() ,
,![]() ;
;
(2) 估计使用10年时,维修费用是多少.
| 得 分 | 评卷人 |
21. (本小题满分10分)
已知点A(4,0),B(0,4),C(cosα,sinα),O为坐标原点.
(1) 若![]() ,求sin2α的值;
,求sin2α的值;
(2)
若![]() 且α∈(0,π),求
且α∈(0,π),求![]() 与
与![]() 的夹角.
的夹角.
22. (本小题满分12分)
已知函数f(x)=2acos2x+bsinxcosx,f(0)=2,f(![]() )=
)=![]() +
+![]() .
.
(1) 求f(x)的最大值和最小值;
(2) 对于角α,β,若有α-β≠kπ,k∈Z,且f(α)=f(β),求tan(α+β)的值.
济南市高一新课程质量检测(2008.7)数学试题参考答案
一、选择题1. A 2. C 3. B 4. B 5. D 6. C 7. B 8. D 9. A 10. A 11. D 12. C
 二、填空题13.
二、填空题13.![]() 14. 4 15. (-2,-3) 16.
14. 4 15. (-2,-3) 16. ![]()
三、解答题
17. 解:(1) sinα=![]() ……………2分
……………2分
tanα= …………………………………4分
…………………………………4分
(2) 原式=![]() ………8分
………8分
18. 评分细则:共7个空和两条线,开始与结束共1分,两条线1分,其余每空1分.
19. 解:(1) 基本事件空间Ω={(A1,B1,C1),(A1,B1,C2),(A1,B2,C1),A1,B2,C2},(A1,B3,C1),
(A1,B3,C2),(A1,B4,C1),(A1,B4,C2),(A2,B1,C1),(A2,B1,C2),(A2,B2,C1),(A2,B2,C2),(A2,B3,C1),(A2,B3,
C2),(A2,B4,C1),(A2,B4,C2)}共16个………………………………………………………………4分
其中B4被选中的事件有4个…………………………………………………………………5分
所以B4被选中的事件的概率为![]() =
=![]() ……………………………………………6分
……………………………………………6分
(2)
A1和C1全被选中的事件共4个,它的概率为![]() …………………………………………7分
…………………………………………7分
(3)
所以A1和C1不全被选中的概率为1-![]() =
=![]() ………………………………………………8分
………………………………………………8分
(4) 或A1和C1不全被选中的事件共12个……………………………………………………7分
所以概率为![]() …………………………………………………………………………8
…………………………………………………………………………8
| 序号 | x | y | xy | x2 |
| 1 | 2 | 2.2 | 4.4 | 4 |
| 2 | 3 | 3.8 | 11.4 | 9 |
| 3 | 4 | 5.5 | 22.0 | 16 |
| 4 | 5 | 6.5 | 32.5 | 25 |
| 5 | 6 | 7.0 | 42.0 | 36 |
| ∑ | 20 | 25 | 112.3 | 90 |
20. 解:(1) 填表………………………………………4分
所以![]()
将其代入公式得
![]()
![]() ………………6分
………………6分
(2)
线性回归方程为![]() =1.23x+0.08…………7分x=10时,
=1.23x+0.08…………7分x=10时,![]() =1.23x+0.08=1.23×10+0.08=12.38
=1.23x+0.08=1.23×10+0.08=12.38
(万元)…………………………………………………………………………………………9分
答:使用10年维修费用是12.38(万元)……………………………………………………10分
21. 解:(1)
![]() =(cosα-4,sinα),
=(cosα-4,sinα),![]() =(cosα,sinα-4)…………………………………1分
=(cosα,sinα-4)…………………………………1分
由![]() =-2,得cosα(cosα-4)+sinα·(sinα-4)=-2
=-2,得cosα(cosα-4)+sinα·(sinα-4)=-2
化简得sinα+cosα=![]() ……………………………………………………………………4分
……………………………………………………………………4分
两边平方得1+2sinαcosα=![]() …………………………………………………………5分
…………………………………………………………5分
所以sin2α=-![]() …………………………………………………………………………6分
…………………………………………………………………………6分
(2)
由![]() ……………………7分
……………………7分
![]()
平方得cosα=![]() …………………………………………………………………………8分
…………………………………………………………………………8分
∵α∈(0,π),∴α=![]() ,C
,C
∴cos<![]() >=
>=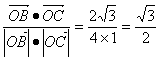 ………………………………………9分
………………………………………9分
∴<![]() >=
>=![]() ……………………………………………………………………10分
……………………………………………………………………10分
22. 解:(1) 由f(0)=2a=2得a=1,…………………………………………………………1分
由f(![]() )=2×
)=2×![]() +b·
+b·![]() ×
×![]() =
=![]() +
+![]() 得b=2………………………………………2分
得b=2………………………………………2分
于是f(x)=2acos2x+bsinxcosx=2cos2x+sin2x=cos2x+sin2x+1
=![]() sin(2x+
sin(2x+![]() )+1……………………………………………………………………4分
)+1……………………………………………………………………4分
∴f(x)的最大值和最小值分别为![]() ………………………………………6分
………………………………………6分
(2)
∵f(α)=f(β),∴sin(2α+![]() )=sin(2β+
)=sin(2β+![]() )………………………………7分
)………………………………7分
∴得①2α+![]() =2kπ+2β+
=2kπ+2β+![]() 或②2α+
或②2α+![]() =2kπ+π-(2β+
=2kπ+π-(2β+![]() )……………………9分
)……………………9分
由①得α-β=kπ,k∈Z(舍去)………………………………………………………10分
由②得α+β=kπ+![]() ,k∈Z……………………………………………………………11分
,k∈Z……………………………………………………………11分
∴tan(α+β)=tan(kπ+![]() )=1…………………………………………………………12分
)=1…………………………………………………………12分