高一数学第二学期期末质量调研试题2008.7
命题单位:常州市教育教研室
一、填空题:本大题共14小题,每小题3分,共42分.不需写出解答过程,请把答案填写在题中横线位置上.
1.直线![]() 的倾斜角等于
.
的倾斜角等于
.
2.函数![]() 的定义域为
.
的定义域为
.
3.圆心是![]() ,且经过原点的圆的标准方程为
.
,且经过原点的圆的标准方程为
.
4.如果直线![]() 与
与![]() 互相垂直,那么实数m=
.
互相垂直,那么实数m=
.
5.已知△ABC的三个顶点![]() ,
,![]() ,
,![]() ,则BC 边上的中线长等于
.
,则BC 边上的中线长等于
.
6.已知等差数列![]() 的首项
的首项![]() ,
,![]() ,则
,则![]() 的公 差d= .
的公 差d= .
7.正方体![]() 中,异面直线
中,异面直线![]() 所成角的大小为 .
所成角的大小为 .
8.设![]() 为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
为两两不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
①若![]() 则
则![]()
 ②
②![]() 则
则![]()
③![]() 则
则 ![]() ;
;
④若![]() 则
则![]()
则其中所有正确命题的序号是 .
9.一个空间几何体的主视图、左视图、俯视图为直角三角形,边
长如右图所示,那么该几何体的体积为 .
10.棱长为1的正方体外接球的表面积为 .
11.已知实数![]() 、
、![]() 满足约束条件
满足约束条件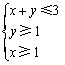 ,则
,则![]() 的最小值为 .
的最小值为 .
12.设正数![]() 满足
满足![]() ,则
,则![]() 的最大值为
.
的最大值为
.
13.若直线y=x+m与曲线x=![]() 有且只有一个公共点,则实数m的取值范围是 .
有且只有一个公共点,则实数m的取值范围是 .
14.汽车轮胎的磨损与汽车行驶的距离成正比,已知某品牌的前轮轮胎可行驶的里程为![]() 千米,后轮轮胎可行驶
千米,后轮轮胎可行驶![]() 千米,
千米,![]() .若在行驶一定的里程之后,将前后的两对轮胎互换,则可增加行驶的里程数,那么一套新的轮胎最多可以保证行驶的里程是 千米.
.若在行驶一定的里程之后,将前后的两对轮胎互换,则可增加行驶的里程数,那么一套新的轮胎最多可以保证行驶的里程是 千米.
二.解答题:本大题共6小题,共58分.解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分8 分)如图,P,Q,R分别是三棱椎A—BCD的棱AC,BC,BD的中点,过三点P,Q,R的平面交AD于S.
求证:四边形PQRS是平行四边形.
16.(本小题满分8 分)
(1)已知直线l过点P(3,4),它在y轴上的截距是在x轴上截距的2倍,求直线l的方程.
(2)求与圆C:![]() 同圆心,且与直线2x–y+1=0相切的圆的方程.
同圆心,且与直线2x–y+1=0相切的圆的方程.
17.(本小题满分 10分)
设等差数列![]() 的前
的前![]() 项和为
项和为![]() , 已知
, 已知![]() .
.
(1)求![]() 的首项
的首项![]() 和公差
和公差![]() 的值;
的值;
(2)若![]() ,求数列
,求数列![]() 的前n项和.
的前n项和.
18.(本小题满分10 分)
若关于x的不等式![]() 在[-1,3]上恒成立,求实数m的取值范围.
在[-1,3]上恒成立,求实数m的取值范围.
19.(本小题满分10 分)
如图,在正方体![]() 中,F为
中,F为![]() 的中点.
的中点.
求证:(1)![]() ;(2)
;(2)![]() .
.
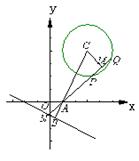
20.(本小题满分 12 分)已知圆![]() ,直线
,直线![]() 过定点 A (1,0).
过定点 A (1,0).
(1)若![]() 与圆C相切,求
与圆C相切,求![]() 的方程;
的方程;
(2)若![]() 的倾斜角为
的倾斜角为![]() ,
,![]() 与圆C相交于P,Q两点,求线段PQ的中点M的坐标;
与圆C相交于P,Q两点,求线段PQ的中点M的坐标;
(3)若![]() 与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时
与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时![]() 的直线方程.
的直线方程.
常州市2007—2008学年度第二学期期末质量调研
高一数学(必修5必修2)试题答案
一.填空题:
1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.3
6.3 7.
5.3
6.3 7.![]() 8.②③
9.1 10.
8.②③
9.1 10.![]() 11.2 12.
11.2 12.![]() 13.
13.![]() 14.
14.![]()
二.解答题:
15.证明:
∵P为AC的中点,Q 为BC的中点,
∴PQ∥AB,且PQ=![]() AB. …………………………………………1分
AB. …………………………………………1分
![]()
∴AB∥ 平面PQRS. …………………………………………3分
![]()
∴AB∥RS. …………………………………………5分
∵R为BD中点,
∴S为AD中点. …………………………………………6分
∴RS∥AB,且RS=![]() AB.
AB.
∴RS∥PQ,且RS=PQ.
∴PQRS为平行四边形. …………………………………………8分
16.解:
(1)当直线l过原点时,斜率k=![]() ,直线方程为
,直线方程为![]() . ………………2分
. ………………2分
(2)当直线l不过原点时,设直线方程为![]() .
.
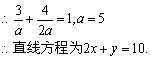
∴所求直线l方程为![]()
(2)

17解: (1)![]()
![]() ,
, ![]() …………………………………3分
…………………………………3分
解得![]() …… ……………………………………………………………5
分
…… ……………………………………………………………5
分
(2)
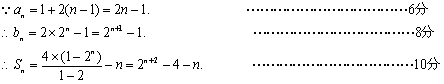
18解:

19证明:连接AC,设![]() .
.

(2)设正方体棱长为 a.

20.
(1) 解:①若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() ,符合题意.
…………………1 分
,符合题意.
…………………1 分
②若直线![]() 斜率存在,设直线
斜率存在,设直线![]() 为
为![]() ,即
,即![]() .
.
由题意知,圆心(3,4)到已知直线![]() 的距离等于半径2,即:
的距离等于半径2,即: ![]() ,
,
解之得
![]() .
.
所求直线方程是![]() ,或
,或![]() . …………………………………… 3分
. …………………………………… 3分
(2) 直线![]() 方程为y=x-1.
方程为y=x-1.
∵PQ⊥CM,
∴CM方程为y-4=-(x-3),即x+y-7=0.
∵![]()
∴![]()
∴M点坐标(4,3). ……………………………………6
 (3)
直线与圆相交,斜率必定存在,且不为0,设直线方程为
(3)
直线与圆相交,斜率必定存在,且不为0,设直线方程为![]() ,
,
则圆![]()
![]() 积
积
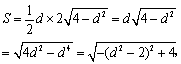
∴当d=![]() 时,S取得最小值2.
…………………………………9分
时,S取得最小值2.
…………………………………9分
![]()
∴直线方程为y=x-1,或y=7x-7. …………………………………12分