高一数学第二学期期终试题
一.选择题:(本大题共12个小题,每小题4分,共48分)在每个小题的4个选项中,只有一个符合题目要求,请把所选项填在下表中。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1.下列说法正确的是
(A)第一象限角是锐角 (B)-1200是钝角
(C)1850和-1750是终边相同角 (D)![]() 的终边相同的角是2k
的终边相同的角是2k![]() (k
(k![]() R)
R)
2.下列命题中,正确命题的个数为: ( 1 )![]()
![]() ( 2 )
( 2 )![]()
( 3 )![]() ( 4)(
( 4)(![]() A.1个 B.2 个C.3个D.4 个
A.1个 B.2 个C.3个D.4 个
3.函数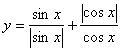 的值域是:( A ){2} ( B ){0,2}( C ){-2,2} ( D ){-2,0,2}
的值域是:( A ){2} ( B ){0,2}( C ){-2,2} ( D ){-2,0,2}
4设O是正六边形ABCDEF的中心,则下列命题中,正确命题的个数为:
①![]()
![]() 与
与 ![]() 共线②
共线②![]() ③
③![]() ④
④![]() //
//![]()
A.1个 B. 2个 C.3个 D. 4个
5.函数![]() 的最小正周期是:
的最小正周期是:
A. ![]() B.
B.
![]() C.
C. ![]() D.
D.![]()
6函数 ![]() 的一条对称轴是
的一条对称轴是
A. ![]() B.
B.![]() C.
C. ![]() D.
D.![]()
7.已知![]()
![]()
8.在三角形ABC中,记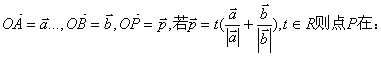
A.AB所在直线上 B.角AOB的角平分线上 C.线段AB的中垂线上 D.AB边的中线上
9.已知函数![]() 的大小,正确的是:
的大小,正确的是:
A, f(-1)<f(2)<f(3) B.f(-1)<f(3)<f(1) C. f(3)<f(-1)<f(1) D.f(3)<f(1)<f(-1)
10.在三角形ABC中,a=4 ,c=2![]() ,B=1500
则b等于:
,B=1500
则b等于:
A.2 B。2![]() C。2
C。2![]() D。2
D。2![]()
11.已知A(-3,3),B(-1,1),C(1,y)三点共线,则y等于:A-1 B1 C 2 D5
12.设函数 y=f(x) 的图像为 C1 ,将C1向右平移 ![]() 个单位,可得曲线 C2 ,若曲线 C2与函数y=cos2x 的图像关于x轴对称,那么y=f(x)的解析式可能是:
个单位,可得曲线 C2 ,若曲线 C2与函数y=cos2x 的图像关于x轴对称,那么y=f(x)的解析式可能是:
A.f(x)=sin2x
B.f(x)=cos2x C.
f(x)=-sin2x
D.f(x)=-cos(2x-![]() )
)
二.填空题:(共4个小题,每小题4分,共16分)
13.已知cosa=-![]() , a 为钝角,则a=________________
, a 为钝角,则a=________________
14.函数 f(x)=sinx+cosx 的最大值为________________
15.已知![]() 若
若 ![]() 与
与 ![]() 的夹角为900 ,则x=____________
的夹角为900 ,则x=____________
16.已知cosa=
-![]() ,且
,且![]() <a<
<a<![]() 求tan(
求tan(![]() 的值____________
的值____________
三.解答题(本大题有5个小题,共56分)
17.(10分)
化简: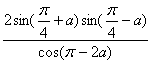
18.(10分)
已知cosa=-![]() ,且a为第三象限角,求cos(a+
,且a为第三象限角,求cos(a+![]() ) 的值.
) 的值.
19.(12分)已知函数:f(x)=![]() 且
且![]()
⑴求f(x)的最小正周期;⑵若函数y=2sin2x的图像按向量![]() <
<![]() ), 平移后得到 y=f(x) 的图像,求实数m、n的值。
), 平移后得到 y=f(x) 的图像,求实数m、n的值。
20.已知![]() 且
且![]()
⑴ 求![]() 与
与![]() 的夹角。⑵求
的夹角。⑵求![]() 与
与![]()
21.(本小题满分12分)
在![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)若![]() 最大边的边长为
最大边的边长为![]() ,求最小边的边长.
,求最小边的边长.
2007-2008高一第二学期期终预考试题答案
一.选择题:(本大题共12个小题,每小题4分,共48分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 答案 | C | B | D | C | B | D | A | B | C | B | A | A |
二.填空题:(共4个小题,每小题4分,共16分)
13、![]() 14、
14、![]() 15: 9 16:
15: 9 16: ![]()
三.解答题(本大题有5个小题,共56分)
17(10分)解:原式=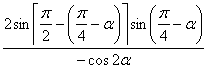 …………..3分
…………..3分![]()
=![]()
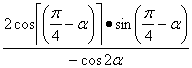 ……………5分
……………5分
=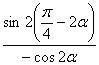 ………………………………7分
………………………………7分
=![]() =-1………………………………10分
=-1………………………………10分
18.(10分) )解:因为cosa=-![]() ,a为第三象限角
,a为第三象限角
所以sina=-![]()
![]() …………………………………4分
…………………………………4分
所以cos(a+![]() )=cosacos
)=cosacos![]() -sinasin
-sinasin![]()
=![]()
=![]() ………………10分
………………10分
19.(12分) 解⑴f(x)=![]() 2cos2x+
2cos2x+![]()
=1+cos2x+![]() ………4分
………4分
所以T=![]() ………5分
………5分
⑵设函数y=2sin2x的图像上任意一点(x,y)按向量![]() <
<![]() ), 平移后对应的点为(x`,y`)则:
), 平移后对应的点为(x`,y`)则:
![]() x`=x+m y`=y+n … 6分 所以x=x`-m y=y`-n
x`=x+m y`=y+n … 6分 所以x=x`-m y=y`-n
所以y`-n=2sin2(x`-m) 所以y`=2sin2(2x`-2m)+n *…8分
由⑴可知函数*的解析式为y=2sin(2x+![]() )+1
)+1
故可令-2m=![]() n=1 ………………………10分
n=1 ………………………10分
得m=-![]() n=1 可满足
n=1 可满足![]() <
<![]()
故实数m、n的值分别为-![]() ,1……………………12分
,1……………………12分
20.(12分)解⑴因为(2![]()
所以6![]() 2-7
2-7![]() 2=21
2=21
又因为![]()
所以![]() ………………………………3分
………………………………3分
所以cos<![]() 〉=
〉= ………………………………5分
………………………………5分
所以〈![]() 〉=
〉=![]() ………………………………6分
………………………………6分
⑵由⑴有![]() ………………………………9分
………………………………9分
![]() ………………………………12分
………………………………12分
21.解:(Ⅰ)![]() ,…………………2分
,…………………2分
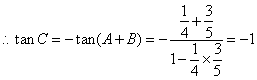 .又
.又![]() ,
,![]() .……5分
.……5分
(Ⅱ)![]() ,
,![]() 边最大,即
边最大,即![]() .……7分
.……7分
又![]() ,
,![]() 角
角![]() 最小,
最小,![]() 边为最小边.
边为最小边.
由 且
且![]() ,……9分
,……9分
得![]() .由
.由![]() 得:
得:![]() .
.
所以,最小边![]() .……12分
.……12分