高一数学第二学期第一阶段考试试卷
(本卷满分160分,时间:120分钟)
一.填空题(本大题共14小题,每小题5分,共70分)
1. 等差数列![]() 中,
中,![]() ,则
,则![]() =__________
=__________
2. 在△ABC中,若a = 2 ,![]() ,
,![]() , 则B等于
, 则B等于
3. 已知实数![]() 、
、![]() 满足约束条件
满足约束条件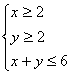 ,则
,则![]() 的最大值为
的最大值为
4. 若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 _____
,则此数列的通项公式为 _____
5. 等比数列{an}的前n项的和为48,前2n项的和为60,则它的前3n项的和为_________![]()
6. △ABC的内角A、B、C的对边分别是a、b、c,若a、b、c成等比数列,且c=
7.已知等比数列![]() 的各项均为正数,公比
的各项均为正数,公比![]() ,设
,设![]() ,
,![]() ,则P与Q的大小关系是_____________________
,则P与Q的大小关系是_____________________
8. 在![]() ABC中,
ABC中,![]() ,
,![]() ,面积为
,面积为![]() ,那么
,那么![]() 的长度为 .
的长度为 .
9. 首项为-24的等差数列,从第10项起开始为正数,则公差的取值范围是____________
10.若不等式![]() 和不等式
和不等式![]() 的解集相同,则
的解集相同,则![]() -
-![]() 的值为
的值为
11. 等差数列![]() 共有
共有![]() 项,其中奇数项之和为319,偶数项之和为290,则其中间项为_______________.
项,其中奇数项之和为319,偶数项之和为290,则其中间项为_______________.
12. 等差数列{an}
中,Sn是它的前n项和,且![]() ,则①此数列的公差d<0
②S9<S6 ③a7是各项中最大的一项 ④S7一定是Sn中的最大值。其中正确的是________(填序号)
,则①此数列的公差d<0
②S9<S6 ③a7是各项中最大的一项 ④S7一定是Sn中的最大值。其中正确的是________(填序号)
13.已知a>0,b>0,且![]() ,则
,则![]() 的最大值是
的最大值是
 14.如图,在面积为1的正
14.如图,在面积为1的正![]() 内作正
内作正![]() ,使
,使![]() ,
,![]() ,
,![]() ,依此类推, 在正
,依此类推, 在正![]() 内再作正
内再作正![]() ,……。记正
,……。记正![]() 的面积为
的面积为![]() ,
,
则a1+a2+……+an=__________________
二.解答题(本大题共6小题,共90分)
15.(本题12分)求不等式组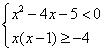 的解集。
的解集。
16. (本题12分)在等比数列![]() 的前n项和中,
的前n项和中,![]() 最小,且
最小,且![]() ,前n项和
,前n项和![]() ,求n和公比q
,求n和公比q
17(本题14分)设数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数y=-x+12的图像上.
均在函数y=-x+12的图像上.
(Ⅰ)写出![]() 关于n的函数表达式;
关于n的函数表达式;
(Ⅱ)求证:数列![]() 是等差数列.
是等差数列.
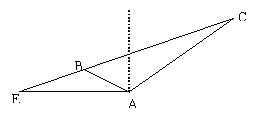 18.(本题14分)小明在某岛上的A处,上午11时测得在A的北偏东600的C处有一艘轮船,12时20分时测得该船航行到北偏西600的B处,12时40分时又测得轮船到达位于A正西方
18.(本题14分)小明在某岛上的A处,上午11时测得在A的北偏东600的C处有一艘轮船,12时20分时测得该船航行到北偏西600的B处,12时40分时又测得轮船到达位于A正西方
(1)点B到A的距离;
(2)船的航行速度。
19.(本题18分)已知正数数列![]() 中,
中, ![]() (
(![]() ), a1=1,
), a1=1,
(1)求a2,a3;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]()
20.(本题20分)已知数列![]() 的前
的前![]() 项和为
项和为![]() 满足
满足![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,判断
,判断![]() 是什么数列,并说明理由;
是什么数列,并说明理由;
(Ⅲ)证明:![]()
新华中学高一数学试卷答题纸
一.填空题
1._______________________________ 2._____________________________
3._______________________________ 4._____________________________
5._______________________________ 6._____________________________
7._______________________________ 8._____________________________
9._______________________________ 10._____________________________
11._____________________________ 12._____________________________
13.______________________________ 14._____________________________
二.解答题
15.
16.
17.
18.
 |
| 座位号 |
19.
20.
高一数学试卷第二学期第一阶段考试
答案
一.填空题
1.8;2.![]() ;3.20;4.
;3.20;4.![]() ;5.63;6.
;5.63;6.![]() ;7.
;7.![]() ;
;
8.![]() ;9.
;9.![]() ;10.5;11.29;12.①②④;13.
;10.5;11.29;12.①②④;13.![]() ;14.
;14.![]()
二.解答题
15.(本题12分)求不等式组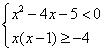 的解集。
的解集。
解:![]() ;-------------------------5分
;-------------------------5分
![]() --------------------------------10分
--------------------------------10分
所以不等式组的解集为![]() ----------------------------12分
----------------------------12分
16. 在等比数列![]() 的前n项和中,
的前n项和中,![]() 最小,且
最小,且![]() ,前n项和
,前n项和![]() ,求n和公比q
,求n和公比q
解:由题意,因为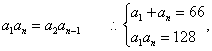 -----------------------4分
-----------------------4分
解得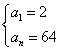 或
或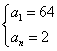 --------------------------------------6分
--------------------------------------6分
![]() -------------------------------------8分
-------------------------------------8分
依题意知![]()
![]() ------------------------------10分
------------------------------10分
![]() ---------------------------------------------12分
---------------------------------------------12分
17(本题14分)设数列![]() 的前n项和为
的前n项和为![]() ,点
,点![]() 均在函数y=-x+12的图像上.(Ⅰ)写出
均在函数y=-x+12的图像上.(Ⅰ)写出![]() 关于n的函数表达式; (Ⅱ)求证:数列
关于n的函数表达式; (Ⅱ)求证:数列![]() 是等差数列.
是等差数列.
解:(1)由条件,![]() , ---------------------------------4分
, ---------------------------------4分
即![]() -----------------------------------
6分
-----------------------------------
6分
(2)![]()
![]() --------------------------------10分
--------------------------------10分
![]() 为常数------------12分
为常数------------12分
又![]()
![]() ,所以
,所以![]() 是等差数列------14分
是等差数列------14分
注:其他证法请酌情给分
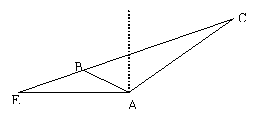
 18.(本题14分)小明在某岛上的A处,上午11时测得在A的北偏东600的C处有一艘轮船,12时20分时测得该船航行到北偏西600的B处,12时40分时又测得轮船到达位于A正西方
18.(本题14分)小明在某岛上的A处,上午11时测得在A的北偏东600的C处有一艘轮船,12时20分时测得该船航行到北偏西600的B处,12时40分时又测得轮船到达位于A正西方
(1)点B到A的距离;
(2)船的航行速度。
解:(1)由已知得BC=4BE,设BE=x,则BC=4x,
------------------2分
在![]() 中,由正弦定理得
中,由正弦定理得
![]() ---------------------6分
---------------------6分
在![]() 中,由正弦定理得
中,由正弦定理得
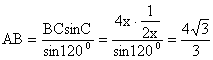 --------------------------8分
--------------------------8分
(2)在![]() 中,由余弦定理得
中,由余弦定理得
![]()
所以![]() ------------------------------------------12分
------------------------------------------12分
所以轮船速度是![]() (千米/小时)----------------14分
(千米/小时)----------------14分
19.(本题18分)已知正数数列![]() 中,
中, ![]() (
(![]() ), a1=1,
), a1=1,
(1)求a2,a3;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]()
解:(1)![]() ---------------------------------------4分
---------------------------------------4分
(2)由条件![]() -----------------------6分
-----------------------6分
因为![]() ,所以
,所以![]()
![]() --------8分
--------8分
![]() 是以1为首项,2为公比的等比数列
是以1为首项,2为公比的等比数列
![]() -------------------------------------10分
-------------------------------------10分
(3)由条件![]()
![]() ----------------------12分
----------------------12分
![]()
![]() ------------------14分
------------------14分
两式相减得:![]() ---------------16分
---------------16分
可得:![]() -------------------------18分
-------------------------18分
20.(本题20分)已知数列![]() 的前
的前![]() 项和为
项和为![]() 满足
满足![]()
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,判断
,判断![]() 是什么数列,并说明理由;
是什么数列,并说明理由;
(Ⅲ)证明:![]()
解:(1)由条件![]()
![]() ,
,![]() ……………………4分
……………………4分
故数列![]() 是首项为2,公比为2的等比数列。……………………5分
是首项为2,公比为2的等比数列。……………………5分
![]() ,
,![]() …………………………………………6分
…………………………………………6分
(2)数列![]() 是等差数列……………………………………8分
是等差数列……………………………………8分
![]() ,
,![]()
![]() ①
①
![]() ②
②
②—①得![]() ,即
,即![]() ③……………10分
③……………10分
![]() ④
④
④—③得![]() ,即
,即![]()
所以数列![]() 是等差数列…………………………………………………………12分
是等差数列…………………………………………………………12分
(3)![]() ………………………………16分
………………………………16分
设![]() ,则
,则![]()
![]()
…………18分
![]() ………………………………20分
………………………………20分