高一数学第二学期第二次月考试题(必修2+必修5)
注:本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页,满分150分。 答
题时间120分钟。必须将答案全部写在答题卷上,否则一律无效。
第Ⅰ卷(选择题)
一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请把答案填写在答题纸上)
1、已知集合![]() ,则集合
,则集合![]()
中元素的个数为
A、0 B、1 C、2 D、不确定
2、若等差数列![]() 的前3项和
的前3项和![]() ,则
,则![]() 等于
等于
A、3 B、4 C、5 D、6
3、已知![]() 的面积为
的面积为![]() ,且
,且![]() ,则
,则![]() 等于
等于
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已知![]() 为两条不同的直线,
为两条不同的直线,![]() 为两个不同的平面,则下列命题中正确
为两个不同的平面,则下列命题中正确
的是
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、直线![]() 的倾斜角的范围是
的倾斜角的范围是
A、![]() B、
B、![]()
C、![]() D、
D、![]()
 6、在小时候,我们就用手指练习过数数. 一个小朋友按如图所示的规则练习
6、在小时候,我们就用手指练习过数数. 一个小朋友按如图所示的规则练习
数数,数到2008时对应的指头是
A、大拇指
B、食指
C、中指
D、无名指
7、在![]() 中,
中,![]() ,则
,则![]() 等于
等于
A、![]() B、
B、![]() C、
C、![]() D、以上都不对
D、以上都不对
8、已知一个几何体的三视图如下图所示,则此几何体的表面积为
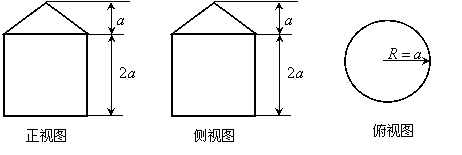
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、在下列表格中,每格填上一个数字后,使每一横行成等差数列,每一纵列
成等比数列,则![]() 的值为
的值为
| 1 | 2 | |||
|
| 1 | |||
|
| ||||
|
| ||||
|
|
A、1 B、2 C、3 D、4
10、在等差数列![]() 中,
中,![]() ,
,![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项
项
和,则使![]() 的
的![]() 的最小值为
的最小值为
A、10 B、11 C、20 D、21
11、从点![]() 向圆
向圆![]() 作切线,切线长度的最小值等于
作切线,切线长度的最小值等于
A、4 B、![]() C、5 D、
C、5 D、![]()
12、在![]() 的二面角
的二面角![]() 内有一点
内有一点![]() ,点
,点![]() 到两个面
到两个面![]() 的距离都为
的距离都为![]() ,则点
,则点![]() 到棱
到棱![]() 的距离为
的距离为
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
宣城中学07—08学年度第二学期第二次月考
高一数学答题卷
一、选择题:(本题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
 第Ⅱ卷(非选择题)
第Ⅱ卷(非选择题)
二、填空题:(本题共4小题,每小题4分,共16分)
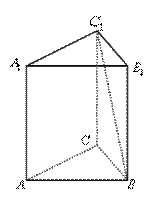
13、如图,在正三棱柱![]() 中,侧棱长为
中,侧棱长为![]() ,底面三角形
,底面三角形
的边长为![]() ,则
,则![]() 与侧面
与侧面![]() 所成的角为
。
所成的角为
。
14、若直线![]() 与曲线
与曲线![]() 恰有一个公共点,则实数
恰有一个公共点,则实数![]()
的取值范围是 。
15、在![]() 中,若
中,若![]() ,则
,则![]() 为
三角形。
为
三角形。
16、已知![]() 为等比数列,且
为等比数列,且![]() ,那么
,那么![]() 。
。
三、解答题:(本题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17、(本小题满分12分)
一条直线从点![]() 射出,经
射出,经![]() 轴反射后,与圆
轴反射后,与圆![]() 相切,求反射后光线所在直线的方程。
相切,求反射后光线所在直线的方程。
18、(本小题满分12分)
有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.
19、(本小题满分12分)
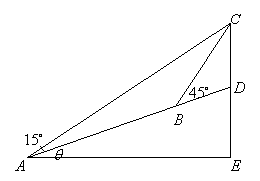 如右图,在斜度一定的山坡上的一点
如右图,在斜度一定的山坡上的一点![]() 测得山顶上一建筑物顶端
测得山顶上一建筑物顶端![]() 对于山坡的斜度为
对于山坡的斜度为![]() ,向山顶前进
,向山顶前进![]() 后,又从
后,又从![]() 点测得斜度为
点测得斜度为![]() ,设建筑物的高度为
,设建筑物的高度为 ,求此山对于地平面的斜度的倾角
,求此山对于地平面的斜度的倾角![]() .
.
20、(本小题满分12分)
已知在等比数列![]() 中,
中,![]() ,设
,设![]() .
.
(Ⅰ)求数列![]() 的通项; (Ⅱ)求数列
的通项; (Ⅱ)求数列![]() 前
前![]() 项和
项和![]() 的最大值.
的最大值.
21、(本小题满分13分)
海岛![]() 上有一座海拔
上有一座海拔![]() 的小山,山顶设有一观察站
的小山,山顶设有一观察站![]() ,上午
,上午![]() 时测得一轮船在海岛的北偏东
时测得一轮船在海岛的北偏东![]() 的
的![]() 处,俯角为
处,俯角为![]() ,
,![]() 时
时![]() 分,又测得该船在海岛的北偏西
分,又测得该船在海岛的北偏西![]() 的
的![]() 处,俯角为
处,俯角为![]() .
.
(Ⅰ) 求该船的速度;
(Ⅱ)若此船以不变的船速继续前进,则它何时到达海岛的正西方向?此时轮船所在点![]() 离海岛
离海岛![]() 的距离是多少?
的距离是多少?
22、(本小题满分13分)
设数列![]() 的前
的前![]() 项和
项和![]() ,
,![]() 为等比数列,且
为等比数列,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 前
前![]() 项和
项和![]() .
.
宣城中学07—08学年度第二学期第二次月考
高一数学答题卷
一、选择题:(本题共12小题,每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | A | D | D | B | B | C | C | A | C | B | A |
 第Ⅱ卷(非选择题)
第Ⅱ卷(非选择题)
二、填空题:(本题共4小题,每小题4分,共16分)
13、如图,在正三棱柱![]() 中,侧棱长为
中,侧棱长为![]() ,底面三角形
,底面三角形
的边长为![]() ,则
,则![]() 与侧面
与侧面![]() 所成的角为
所成的角为 ![]() 。
。
14、若直线![]() 与曲线
与曲线![]() 恰有一个公共点,则实数
恰有一个公共点,则实数![]()
的取值范围是 ![]() 。
。
15、在![]() 中,若
中,若![]() ,则
,则![]() 为 等腰直角 三角形。
为 等腰直角 三角形。
16、已知![]() 为等比数列,且
为等比数列,且![]() ,那么
,那么![]() -5 。
-5 。
三、解答题:(本题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17、(本小题满分12分)
一条直线从点![]() 射出,经
射出,经![]() 轴反射后,与圆
轴反射后,与圆![]() 相切,求反射后光线所在直线的方程。
相切,求反射后光线所在直线的方程。
 |
解:由对称性可知:反射光线所在直线一定经过![]() 点关于
点关于![]() 轴的对称点
轴的对称点![]() ,又斜率存在,可设其直线方程为
,又斜率存在,可设其直线方程为![]() ,即
,即![]()
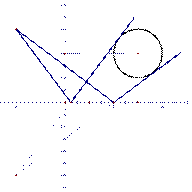 由
由![]() 即
即![]() 可得
可得![]()
故所求直线方程为![]()
或![]()
18、(本小题满分12分)
有四个数,其中前三个数成等差数列,后三个数成等比数列,并且第一个数与第四个数的和是16,第二个数与第三个数的和是12,求这四个数.
 解:由题意设这四个数为
解:由题意设这四个数为![]() ,则
,则
 由(1)得
由(1)得![]() ,
,
代入(2)得![]() ,于是
,于是![]()
当![]() 时,这四个数为
时,这四个数为![]() ;当
;当![]() 时,这四个数为
时,这四个数为![]()
19、(本小题满分12分)
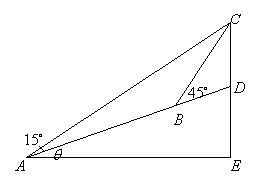 如右图,在斜度一定的山坡上的一点
如右图,在斜度一定的山坡上的一点![]() 测得山顶上一建筑物顶端
测得山顶上一建筑物顶端![]() 对于山坡的斜度为
对于山坡的斜度为![]() ,向山顶前进
,向山顶前进![]() 后,又从
后,又从![]() 点测得斜度为
点测得斜度为![]() ,设建筑物的高度为
,设建筑物的高度为 ,求此山对于地平面的斜度的倾角
,求此山对于地平面的斜度的倾角![]() .
.
 解:在
解:在![]() 中,
中,![]() ,
,
由正弦定理可知,
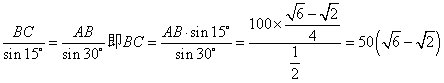
在![]() 中,由正弦定理可知,
中,由正弦定理可知,
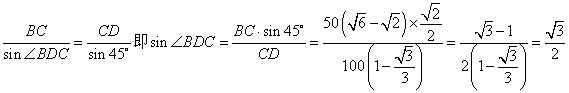
![]() (
(![]() )
) ![]()
答:此山对于地平面的斜度的倾角为![]()
20、(本小题满分12分)
已知在等比数列![]() 中,
中,![]() ,设
,设![]() .
.
 (Ⅰ)求数列
(Ⅰ)求数列![]() 的通项; (Ⅱ)求数列
的通项; (Ⅱ)求数列![]() 前
前![]() 项和
项和![]() 的最大值.
的最大值.

21、(本小题满分13分)
海岛![]() 上有一座海拔
上有一座海拔![]() 的小山,山顶设有一观察站
的小山,山顶设有一观察站![]() ,上午
,上午![]() 时测得一轮船在海岛的北偏东
时测得一轮船在海岛的北偏东![]() 的
的![]() 处,俯角为
处,俯角为![]() ,
,![]() 时
时![]() 分,又测得该船在海岛的北偏西
分,又测得该船在海岛的北偏西![]() 的
的![]() 处,俯角为
处,俯角为![]() .
.
(Ⅰ) 求该船的速度;
(Ⅱ)若此船以不变的船速继续前进,则它何时到达海岛的正西方向?此时轮船所在点![]() 离海岛
离海岛![]() 的距离是多少?
的距离是多少?

 解:(Ⅰ)由题意可知
解:(Ⅰ)由题意可知![]()
![]() ,设
,设![]() ,则
,则
在![]() 中,由余弦定理知
中,由余弦定理知
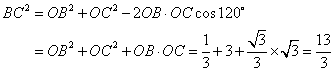
即![]() ,
,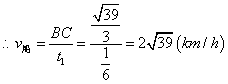
 (Ⅱ)由(Ⅰ)结合正弦定理知
(Ⅱ)由(Ⅰ)结合正弦定理知
在![]() 中由正弦定理知
中由正弦定理知
再由余弦定理知![]()
![]() ,此时
,此时![]()
故该船将于![]() 时
时![]() 分到达海岛的正西方向,轮船所在点
分到达海岛的正西方向,轮船所在点![]() 离海岛
离海岛![]() 的距离是
的距离是![]() .
.
22、(本小题满分13分)
设数列![]() 的前
的前![]() 项和
项和![]() ,
,![]() 为等比数列,且
为等比数列,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
 (Ⅱ)设
(Ⅱ)设![]() ,求数列
,求数列![]() 前
前![]() 项和
项和![]() .
.
解:(Ⅰ)![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故![]() 的通项公式为
的通项公式为![]() 是首项为2,公差为4的等差数列.
是首项为2,公差为4的等差数列.
(Ⅱ) 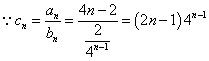 ,
,

两式相减得
![]()
![]()
