充分条件与必要条件·典型例题

 

能力素质

　

例1　已知p：x₁，x₂是方程x²＋5x－6＝0的两根，q：x₁＋x₂＝－5，则p是q的

[　　]

A．充分但不必要条件　 　　B．必要但不充分条件

C．充要条件　 　　　D．既不充分也不必要条件

分析　利用韦达定理转换．

解　∵x₁，x₂是方程x²＋5x－6＝0的两根，

∴x₁，x₂的值分别为1，－6，

∴x₁＋x₂＝1－6＝－5．

因此选A．

说明：判断命题为假命题可以通过举反例．

例2　p是q的充要条件的是

[　　]

A．p：3x＋2＞5，q：－2x－3＞－5

B．p：a＞2，b＜2，q：a＞b

C．p：四边形的两条对角线互相垂直平分，q：四边形是正方形

D．p：a≠0，q：关于x的方程ax＝1有惟一解

分析　逐个验证命题是否等价．

解　对A．p：x＞1，q：x＜1，所以，p是q的既不充分也不必要条件；

对B．pq但qp，p是q的充分非必要条件；

对C．pq且qp，p是q的必要非充分条件；

说明：当a＝0时，ax＝0有无数个解．

例3　若A是B成立的充分条件，D是C成立的必要条件，C是B成立的充要条件，则D是A成立的

[　　]

A．充分条件　 　　　B．必要条件

C．充要条件　 　　　D．既不充分也不必要条件

分析　通过B、C作为桥梁联系A、D．

解　∵A是B的充分条件，∴AB①

∵D是C成立的必要条件，∴CD②

由①③得AC④

由②④得AD．

∴D是A成立的必要条件．选B．

说明：要注意利用推出符号的传递性．

例4　设命题甲为：0＜x＜5，命题乙为x－2＜3，那么甲是乙的

[　　]

A．充分不必要条件　　　 B．必要不充分条件

C．充要条件　 　　　D．既不充分也不必要条件

分析　先解不等式再判定．

解　解不等式x－2＜3得－1＜x＜5．

∵0＜x＜5－1＜x＜5，但－1＜x＜50＜x＜5

∴甲是乙的充分不必要条件，选A．

说明：一般情况下，如果条件甲为x∈A，条件乙为x∈B．

当且仅当A＝B时，甲为乙的充要条件．

例5　设A、B、C三个集合，为使A(B∪C)，条件AB是

[　　]

A．充分条件　 　　　B．必要条件

C．充要条件　 　　　D．既不充分也不必要条件

分析　可以结合图形分析．请同学们自己画图．

∴A(B∪C)．

但是，当B＝N，C＝R，A＝Z时，

显然A(B∪C)，但AB不成立，

综上所述：“AB”“A(B∪C)”，而

“A(B∪C)”“AB”．

即“AB”是“A(B∪C)”的充分条件(不必要)．选A．

说明：画图分析时要画一般形式的图，特殊形式的图会掩盖真实情况．

例6　给出下列各组条件：

(1)p：ab＝0，q：a²＋b²＝0；

(2)p：xy≥0，q：x＋y＝x＋y；

(3)p：m＞0，q：方程x²－x－m＝0有实根；

(4)p：x－1＞2，q：x＜－1．

其中p是q的充要条件的有

[　　]

A．1组　　B．2组

C．3组　　D．4组

分析　使用方程理论和不等式性质．

解　(1)p是q的必要条件

(2)p是q充要条件

(3)p是q的充分条件

(4)p是q的必要条件．选A．

说明：ab＝0指其中至少有一个为零，而a²＋b²＝0指两个都为零．

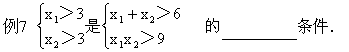
分析　将前后两个不等式组分别作等价变形，观察两者之间的关系．

　

点击思维

　

例8　已知真命题“a≥bc＞d”和“a＜be≤f”，则“c≤d”是“e≤f”的________条件．

分析　∵a≥bc＞d(原命题)，

∴c≤da＜b(逆否命题)．

而a＜be≤f，

∴c≤de≤f即c≤d是e≤f的充分条件．

答　填写“充分”．

说明：充分利用原命题与其逆否命题的等价性是常见的思想方法．

例9　ax²＋2x＋1＝0至少有一个负实根的充要条件是

[　　]

A．0＜a≤1　　 　B．a＜1

C．a≤1　　D．0＜a≤1或a＜0

分析　此题若采用普通方法推导较为复杂，可通过选项提供的信息，用排除法解之．当a＝1时，方程有负根x＝－1，当a＝0时，x＝

当a≠0时

综上所述a≤1．

即ax²＋2x＋1＝0至少有一个负实根的充要条件是a≤1．

说明：特殊值法、排除法都是解选择题的好方法．

例10　已知p、q都是r的必要条件，s是r的充分条件，q是s的充分条件，那么s，r，p分别是q的什么条件？

分析　画出关系图1－21，观察求解．

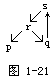
解　s是q的充要条件；(srq，qs)

r是q的充要条件；(rq，qsr)

p是q的必要条件；(qsrp)

说明：图可以画的随意一些，关键要体现各个条件、命题之间的逻辑关系．

例11　关于x的不等式

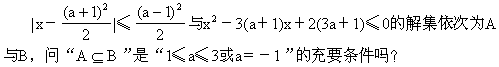
分析　化简A和B，结合数轴，构造不等式(组)，求出a．

解　A＝{x2a≤x≤a²＋1}，B＝{x(x－2)[x－(3a＋1)]≤0}

B＝{x2≤x≤3a＋1}．

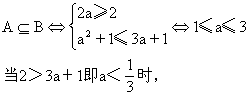
B＝{x3a＋1≤x≤2}

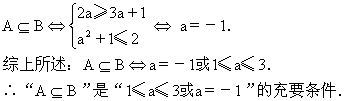
说明：集合的包含关系、命题的真假往往与解不等式密切相关．在解题时要理清思路，表达准确，推理无误．

　

学科渗透

　

要条件？

分析　将充要条件和不等式同解变形相联系．

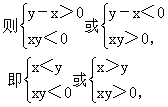
说明：分类讨论要做到不重不漏．

例13　设α，β是方程x²－ax＋b＝0的两个实根，试分析a＞2且b＞1是两根α，β均大于1的什么条件？

分析　把充要条件和方程中根与系数的关系问题相联系，解题时需

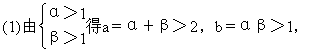
∴qp．

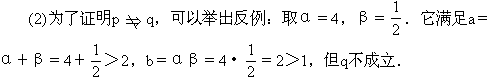
上述讨论可知：a＞2，b＞1是α＞1，β＞1的必要但不充分条件．

说明：本题中的讨论内容在二次方程的根的分布理论中常被使用．

　

高考巡礼

　

例14　(1991年全国高考题)设甲、乙、丙是三个命题，如果甲是乙的必要条件，丙是乙的充分条件，但不是乙的必要条件，那么

[　　]

A．丙是甲的充分条件，但不是甲的必要条件

B．丙是甲的必要条件，但不是甲的充分条件

C．丙是甲的充要条件

D．丙不是甲的充分条件，也不是甲的必要条件

分析1：由丙乙甲且乙丙，即丙是甲的充分不必要条件．

分析2：画图观察之．

答：选A．

说明：抽象命题之间的逻辑关系通常靠画图观察比较方便