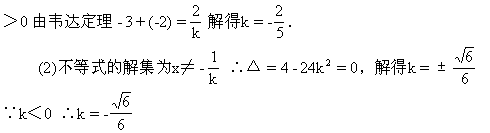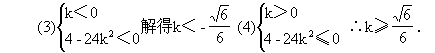§1.5.2一元二次不等式的解法（二）

班级　　　　学号　　　 姓名　　　　　  

目标要点：掌握含字母系数的不等式及恒成立问题的解法。

一、基础练习

1、不等式的解集为{x︱}，则a+b=----------（　　）.

　　 A、-14　　　B、14　　　 C、-10　　　　 D、10

2、已知不等式的解集为，则a的取值范围是----（　  ）

　 A、　　　　  B、　　　　　 C、　　　　 D、

3、若a＞b时，不等式x²-(a+b)x+ab＜0的解集为--------------------（　　）

A．{xx＞a或x＞b}　　　　　　　　　 B．{xx＜a或x＞b}

C．{xa＜x＜b}　　　　　　　　　　　 D．{xb＜x＜a}

4、若方程x²+(m+2)x+m+5=0的两根均为正数，则m的取值范围是______．

5、设不等式对于一切实数都成立，则的范围是___________.

二、能力培养

6、已知集合A={xx²-5x+4≤0}，B={xx²-5x+6≥0}则A∩B=------------（　　）

A．{x1x2或3x4}　　 B．{x1x2，且3x4}

C．{1，2，3，4}　 　　　　　 D．{x-4x-1或2x3}

7、若对于任何实数，二次函数y=ax²-x+c的值恒为负，那么a、c应满足(　　)

A. 且　　　　　　 B、且

　  C、且　　　　　　 D、且

8、不等式的解集为_______________________________.

9、设不等式的解集为A，关于x的不等式的解集为B，若，则实数a组成的集合为______________________.

10、解下列关于x的不等式

　（1）　　　　　　　　 （2）

三、综合拓展

12、设I=R，集合A={x︱},B={x︱},求。

13、已知不等式kx²-2x+6k＜0 (k≠0)

(1)若不等式的解集是｛xx＜-3或x＞-2｝，求k的值．

(3)若不等式的解集是R，求k的值．

　　　　　　　　　　　　　　　 参考答案

1、A　 2、B　 3、D　 4、　 5、　 6、A　 7、C　

 8、　 9、　

10、（1）当时，解集为

　　　　当时，解集为

（2） 当时，解集为R；

当时，解集为

12、=

13、解：(1)由解集x＜-3或x＞-2可知k＜0，不等式变为-kx²+2x-6k