高二数学下第二次半月考试卷

（理科）

注 意 事 项

考生在答题前请认真阅读本注意事项及各题答题要求

1．本试卷共4页，包含填空题(共14题)、解答题(共6题)，满分160分，考试时间为120分钟。

2．答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在答题纸上。

3．请认真核对答题纸密封线内规定填写的项目是否准确。

4．作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置，在其他位置作答一律无效．如有作图需要，可用2B铅笔作答，并请加黑加粗，描写清楚。

一、填空题：本大题共14题，每小题5分，共70分，请将正确答案填写在答题纸的相应位置．

1．多项式（）的展开式中，的系数为　 ▲　 ．

2．点是椭圆上的一个动点，则的最大值为　 ▲　 ．

3．用演绎法证明y=x²是增函数时的大前提是　 ▲　 ．

4．学校要选派4名爱好摄影的同学中的3名参加校外摄影小组的3期培训（每期只派1名），由于时间上的冲突，甲、乙两位同学都不能参加第1期培训，则不同的选派方式有　▲　 种．

5．计算　 ▲　 ．

6．曲线的极坐标方程为，则曲线的直角坐标方程为　 ▲　　．

7．观察下列的算式：1＝1，3＋5＝8，7＋9＋11＝27，13＋15＋17＋19＝64，21＋23＋25＋27＋29＝125，…，从中归纳出一个一般性的结论：　 ▲　 ．

8．一袋中装有5个白球，3个红球，现从袋中往外取球，每次取出一个，取出后记下球的颜色，然后放回，直到红球出现10次停止，设停止时,取球次数为随机变量,则 　 ▲　 ．（只需列式，不需计算结果）

9．已知直线方程为,先进行的变换,再进行的变换, 则变换后其方程为　 ▲　 ．

10．已知复数z满足，则的最小值为 　　　▲　　.

11．设随机事件A、B，，则=　 ▲　 ．

12．下面是按照一定规律画出的一列“树型”图：

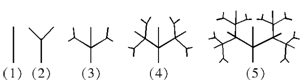
设第个图有个树枝，则与之间的关系是　　　▲　　．

13．设平面内有ｎ条直线，其中有且仅有两条直线互相平行，任意三条直线不过同一点．若用表示这ｎ条直线交点的个数，则当ｎ＞４时，＝　 ▲　 （用含n的数学表达式表示）．

14．设三位数（，其中），若以、、

为三条边的长可以构成一个等腰（含等边）三角形，则这样的三位数有　 ▲　 个．

二、解答题：本大题共6小题；共90分．解答应写出文字说明、证明过程或演算步骤．

15．（本小题满分14分）

男运动员6名,女运动员4名,其中男女队长各1人,从中选5人外出比赛.

（1）若选出男运动员3名,女运动员2名，有多少种不同的选派方法？　　　　　　　 

（2）若队长至少有1人参加，有多少种不同的选派方法？

（3）若至少有1名女运动员，有多少种不同的选派方法？　　　　　 

（4）若既要有队长, 又要有女运动员，有多少种不同的选派方法？

16．（本小题满分14分）

（1）设，若矩阵把直线：变换为另一直线：，求的值.

（2）已知直线经过点,倾斜角，

（I）写出直线的参数方程　

（II）设与圆相交与两点，求点到两点的距离之积　

17．（本小题满分14分）

甲、乙两名射击运动员，甲射击一次命中10环的概率为0.5，乙射击一次命中10环的概率为s，若他们独立的射击两次，设乙命中10环的次数为X，则E(X)=，Y为甲与乙命中10环的次数差的绝对值. 求s的值及Y的分布列及数学期望．

18．（本小题满分16分）

若某一等差数列的首项为，公差为展开式中的常数项，其中m是77⁷⁷-15除以19的余数，则此数列前多少项的和最大？并求出这个最大值。

19．（本小题满分16分）

已知且，．

（1）求函数的表达式；

（2）已知数列的项满足，试求；

（3）猜想的通项，并用数学归纳法证明．

20．(本小题满分16分)

设z是虚数，ω是实数，且－1＜ω＜2．

（1）求 z 的值及z的实部的取值范围；

（2）设，求证：u为纯虚数；

（3）求ω的最小值．

高二数学下第二次半月考试卷

第二次半月考试卷

高二数学

参考答案及评分标准

一、填空题：本大题共14题，每小题5分，共70分，请将正确答案填写在答题纸的相应位置．

1．多项式（）的展开式中，的系数为　 0 　 ．

2．点是椭圆上的一个动点，则的最大值为　　 ．

3．用演绎法证明y=x²是增函数时的大前提是　 增函数的定义　　 ．

4．学校要选派4名爱好摄影的同学中的3名参加校外摄影小组的3期培训（每期只派1名），由于时间上的冲突，甲、乙两位同学都不能参加第1期培训，则不同的选派方式有　12　 种．

5．计算　 　 ．

6．曲线的极坐标方程为，则曲线的直角坐标方程为　 　　．

7．观察下列的算式：1＝1，3＋5＝8，7＋9＋11＝27，13＋15＋17＋19＝64，21＋23＋25＋27＋29＝125，…，从中归纳出一个一般性的结论：　[(n²－n)＋1]＋[(n²－n)＋3]＋[(n²－n)＋5]＋…＋ [(n²－n)＋(2n－1)]＝n³　 ．

8．一袋中装有5个白球，3个红球，现从袋中往外取球，每次取出一个，取出后记下球的颜色，然后放回，直到红球出现10次停止，设停止时,取球次数为随机变量,则 　　 ．（只需列式，不需计算结果）

9．已知直线方程为,先进行的变换,再进行的变换, 则变换后其方程为  4x-y-42=0 　．

10．已知复数z满足，则的最小值为 　　　4　 .

11．设随机事件A、B，，则=　 　 ．

12．下面是按照一定规律画出的一列“树型”图：

设第个图有个树枝，则与之间的关系是　　　　　．

13．设平面内有ｎ条直线，其中有且仅有两条直线互相平行，任意三条直线不过同一点．若用表示这ｎ条直线交点的个数，则当ｎ＞４时，＝（用含n的数学表达式表示）．

14．设三位数（，其中），若以、、

为三条边的长可以构成一个等腰（含等边）三角形，则这样的三位数有　165 　 个．

二、解答题：本大题共6小题；共90分．解答应写出文字说明、证明过程或演算步骤．

15．（本小题满分14分）

男运动员6名,女运动员4名,其中男女队长各1人,从中选5人外出比赛.

（1）若选出男运动员3名,女运动员2名，有多少种不同的选派方法？　　　　　　　 

（2）若队长至少有1人参加，有多少种不同的选派方法？

（3）若至少有1名女运动员，有多少种不同的选派方法？　　　　　 

（4）若既要有队长, 又要有女运动员，有多少种不同的选派方法？

15．解：（1）CC＝120（种）---------------------------------------------------------------------------3分

（2）CC＋CC＝140＋56＝196　（种） -------------------------------------6分

（3）C－C＝246　（种）------------------------------------------------９分

（4）C－C－C＝191　（种）------------------------------------------13分

答：略  -----------------------------------------------------------------------------14分

16．（本小题满分14分）

（1）设，若矩阵把直线：变换为另一直线：，求的值.

（2）已知直线经过点,倾斜角，

（I）写出直线的参数方程　

（II）设与圆相交与两点，求点到两点的距离之积　

16．（1）的值为39

（2）解：（I）直线的参数方程为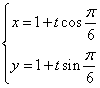，即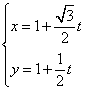

　　　（II）把直线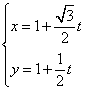代入

得

，则点到两点的距离之积为

17．（本小题满分14分）

甲、乙两名射击运动员，甲射击一次命中10环的概率为0.5，乙射击一次命中10环的概率为s，若他们独立的射击两次，设乙命中10环的次数为X，则E(X)=，Y为甲与乙命中10环的差的绝对值. 求s的值及Y的分布列及数学期望．

17．解：由已知可得，故．

有Y的取值可以是0，1，2.

甲、乙两人命中10环的次数都是0次的概率是，

甲、乙两人命中10环的次数都是1次的概率是，

甲、乙两人命中10环的次数都是2次的概率是

所以；

甲命中10环的次数是2且乙命中10环的次数是0次的概率是，

甲命中10环的次数是0且乙命中10环的次数是2次的概率是

所以，故

所以Y的分布列是

Y	1	2	3
P

　　 所以 Y的期望是EY=

18．（本小题满分16分）

若某一等差数列的首项为，公差为展开式中的常数项，其中m是77⁷⁷-15除以19的余数，则此数列前多少项的和最大？并求出这个最大值。

18．S₂₅=S₂₆=1300

19．（本小题满分16分）

已知且，．

（1）求函数的表达式；

（2）已知数列的项满足，试求；

（3）猜想的通项，并用数学归纳法证明．

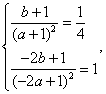19.解:(1)由题意得:即解之得:

所以.

(2); ;

;

.

(1)　  猜想:

证明:①当时, 所以等式成立

②假设且时,等式成立.即.

则当时,

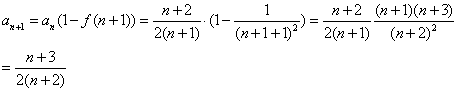
所以,对一切正整数,有

20．(本小题满分16分)

设z是虚数，ω是实数，且－1＜ω＜2．

（1）求 z 的值及z的实部的取值范围；

（2）设，求证：u为纯虚数；

（3）求ω的最小值．

20．解：（1）设，则

，为实数，，，即z=1．---3分

．，的实部的取值范围为．----------------------------5分

　（2），，，为纯虚数-------------------10分

　（3）当，

，即时取到等号，的最小值是1．-----------------16分

第二次半月考答案纸

高二数学（理科）

一．填空题：(本大题共14小题，每小题分，共70分．请把结果直接填在题中横线上)

1. __________________　2. ___________________________

3. __________________　4. ___________________________

5. __________________　6. ___________________________

7. __________________　8. ___________________________

9. __________________　10. __________________________

11. _________________　12. __________________________

13. _________________　14. __________________________

二．解答题：(本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤.)

15.

16.

17.

18.

19．

20.