典型例题一

例1．已知地球的半径为，球面上两点都在北纬45圈上，它们的球面距离为，点在东经30上，求点的位置及两点所在其纬线圈上所对应的劣弧的长度．

分析：求点的位置，如图就是求的大小，只需求出弦的长度．对于应把它放在中求解，根据球面距离概念计算即可．

解：如图，设球心为，北纬45圈的中心为，

由两点的球面距离为，所以=，

为等边三角形．于是．

由，

．即=．

又点在东经30上，故的位置在东经120，北纬45或者西经60，北纬45．

　　两点在其纬线圈上所对应的劣弧．

说明：此题主要目的在于明确经度和纬度概念，及利用球的截面的性质和圆的有关性质设计计算方案．

典型例题二

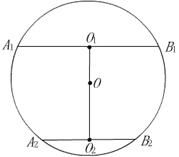例2．用两个平行平面去截半径为的球面，两个截面圆的半径为，．两截面间的距离为，求球的表面积．

分析：此类题目的求解是首先做出截面图，再根据条件和截面性质做出与球的半径有关的三角形等图形，利用方程思想计算可得．

解：设垂直于截面的大圆面交两截面圆于，上述大圆的垂直于的直径交于，如图2．

设，则，解得．

．

说明：通过此类题目，明确球的有关计算问题需先将立体问题转化为平面问题，进一步熟悉有关圆的基础知识，熟练使用方程思想，合理设元，列式，求解．

典型例题三

例3．自半径为的球面上一点，引球的三条两两垂直的弦，求的值．

分析：此题欲计算所求值，应首先把它们放在一个封闭的图形内进行计算，所以应引导学生构造熟悉的几何体并与球有密切的关系，便于将球的条件与之相联．

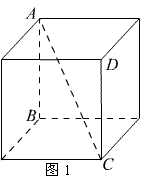
解：以为从一个顶点出发的三条棱，将三棱锥补成一个长方体，则另外四个顶点必在球面上，故长方体是球的内接长方体，则长方体的对角线长是球的直径．

=．

说明：此题突出构造法的使用，以及渗透利用分割补形的方法解决立体几何中体积计算．

典型例题四

例4．试比较等体积的球与正方体的表面积的大小．

分析：首先抓好球与正方体的基本量半径和棱长，找出等量关系，再转化为其面积的大小关系．

解：设球的半径为，正方体的棱长为，它们的体积均为，

则由，，由得．

．

．

，即．

说明：突出相关的面积与体积公式的准确使用，注意比较大小时运算上的设计．

典型例题五

例5．如图1所示，在棱长为1的正方体内有两个球相外切且又分别与正方体内切．（1）求两球半径之和；（2）球的半径为多少时，两球体积之和最小．

分析：此题的关键在于作截面，一个球在正方体内，学生一般知道作对角面，而两个球的球心连线也应在正方体的体对角线上，故仍需作正方体的对角面 ，得如图2的截面图，在图2中，观察与和棱长间的关系即可．

解：如图2，球心和在上，过，分别作的垂线交于．

则由得．

，

．

（1）设两球体积之和为，

则

　　  =

=

当时，有最小值．当时，体积之和有最小值．

典型例题六

例6．设正四面体中，第一个球是它的内切球，第二个球是它的外接球，求这两个球的表面积之比及体积之比．

分析：此题求解的第一个关键是搞清两个球的半径与正四面体的关系，第二个关键是两个球的半径之间的关系，依靠体积分割的方法来解决的．

解：如图，正四面体的中心为，的中心为，则第一个球半径为正四面体的中心到各面的距离，第二个球的半径为正四面体中心到顶点的距离．

设，正四面体的一个面的面积为．

依题意得，

又

即．

所以．．

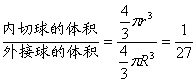说明：正四面体与球的接切问题，可通过线面关系证出，内切球和外接球的两个球心是重合的，为正四面体高的四等分点，即定有内切球的半径(为正四面体的高)，且外接球的半径．

典型例题七

例7．把四个半径都是1的球中的三个放在桌面上，使它两两外切，然后在它们上面放上第四个球，使它与前三个都相切，求第四个球的最高点与桌面的距离．

分析：关键在于能根据要求构造出相应的几何体，由于四个球半径相等，故四个球一定组成正四面体的四个顶点且正四面体的棱长为两球半径之和2．

解：由题意，四球心组成棱长为2的正四面体的四个顶点，

则正四面体的高．

而第四个球的最高点到第四个球的球心距离为求的半径1，且三个球心到桌面的距离都为1，故第四个球的最高点与桌面的距离为．

说明：此类型题目对培养学生空间想象能力，并根据题意构造熟悉几何体都非常有帮助，且还可以适当增加一点实际背景，加强应用意识．

典型例题八

例8　过球面上两点作球的大圆，可能的个数是（　　）．

A．有且只有一个　　　B．一个或无穷多个

C．无数个　　　　　　D．以上均不正确

分析：对球面上两点及球心这三点的位置关系进行讨论．当三点不共线时，可以作一个大圆；当三点共线时，可作无数个大圆，故选B．

答案：B

说明：解此易选出错误判断A．其原因是忽视球心的位置．

典型例题九

例9　球面上有3个点，其中任意两点的球面距离都等于大圆周长的，经过3个点的小圆的周长为，那么这个球的半径为（　　）．

A．　　　B．　　　C．　　　D．

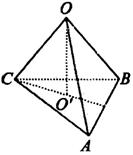
分析：利用球的概念性质和球面距离的知识求解．设球的半径为，小圆的半径为，则，∴．如图所示，设三点、、，为球心，．又∵，∴是等边三角形，同样，、都是等边三角形，得为等边三角形，边长等于球半径．为的外接圆半径，，．

答案：B

说明：本题是近年来球这部分所出的最为综合全面的一道题，除了考查常规的与多面体综合外，还考查了球面距离，几乎涵盖了球这部分所有的主要知识点，是一道不可多得的好题．

典型例题十

例10　半径为的球内接一个各棱长都相等的四棱锥．求该四棱锥的体积．

分析：四棱锥的体积由它的底面积和高确定，只需找到底面、高与球半径的关系即可，解决这个问题的关键是如何选取截面，如图所示．

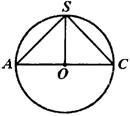
解：∵棱锥底面各边相等，

∴底面是菱形．

∵棱锥侧棱都相等，

∴侧棱在底面上射影都相等，即底面有外接圆．

∴底面是正方形，且顶点在底面上的射影是底面中心，此棱锥是正棱锥．

过该棱锥对角面作截面，设棱长为，则底面对角线，

故截面是等腰直角三角形．

又因为是球的大圆的内接三角形，所以，即．

∴高，体积．

说明：在作四棱锥的截面时，容易误认为截面是正三角形，如果作平等于底面一边的对称截面（过棱锥顶点，底面中心，且与底面一边平行），可得一个腰长为斜高、底为底面边长的等腰三角形，但这一等腰三角形并不是外接球大圆的内接三角形．可见，解决有关几何体接切的问题，如何选取截面是个关键．

解决此类问题的方法通常是先确定多面体的棱长（或高或某个截面内的元素）与球半径的关系，再进一步求解．

典型例题十一

例11　在球面上有四个点、、、，如果、、两两互相垂直，且．求这个球的表面积．

分析：，因而求球的表面关键在于求出球的半径．

解：设过、、三点的球的截面半径为，

球心到该圆面的距离为，

则．

由题意知、、、四点不共面，因而是以这四个点为顶点的三棱锥（如图所示）．的外接圆是球的截面圆．

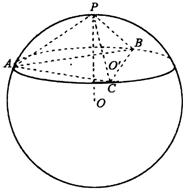
由、、互相垂直知，在面上的射影是的垂心，又，

所以也是的外心，所以为等边三角形，

且边长为，是其中心，

从而也是截面圆的圆心．

据球的截面的性质，有垂直于⊙所在平面，

因此、、共线，三棱锥是高为的球内接正三棱锥，从而．由已知得，，所以，可求得，∴．

说明：涉及到球与圆柱、圆锥、圆台切接问题，一般作其轴截面；涉及到球与棱柱、棱锥、棱台的切接问题，一般过球心及多面体中特殊点或线作截面，把空间问题化为平面问题，进而利用平面几何的知识寻找几何体元素间的关系．

典型例题十二

例12　已知棱长为3的正四面体，、是棱、上的点，且，．求四面体的内切球半径和外接球半径．

分析：可用何种法求内切球半径，把分成4个小体积(如图)．

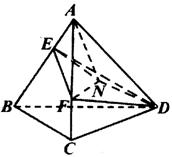
解：设四面体内切球半径为，球心，外接球半径，球心，连结、、、，则．

四面体各面的面积为

，，．

各边边长分别为，，

∴．

∵，

，

∴，

∴．

如图，

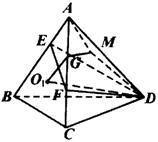
是直角三角形，其个心是斜边的中点．

设中心为，连结，过作平面的垂线，必在此垂线上，

连结、．

∵，，

∴，．

在直角梯形中，，，

，，

又∵，∴，

解得：．

综上，四面体的内切球半径为，外接球半径为．

说明：求四面体外接半径的关键是确定其球心．对此多数同学束手无策，而这主要是因本题图形的背景较复杂．若把该四面体单独移出，则不参发现其球心在过各面三角形外心且与该三角形所在平面垂直的直线上，另还须注意其球心不一定在四面体内部．

本题在求四面体内切球半径时，将该四面体分割为以球心为顶点，各面为底面的四个三棱锥，通过其体积关系求得半径．这样分割的思想方法应给予重视．

典型例题十三

例13　一个倒圆锥形容器，它的轴截面是正三角形，在容器内注入水，并放入一个半径为的铁球，这时水面恰好和球面相切．问将球从圆锥内取出后，圆锥内水平面的高是多少？

分析：先作出轴截面，弄清楚圆锥和球相切时的位置特征，利用铁球取出后，锥内下降部分(圆台)的体积等于球的体积，列式求解．

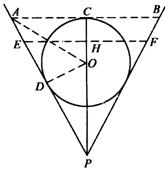
解：如图，作轴截面，设球未取出时，水面高，球取出后，水面高．

∵，，

则以为底面直径的圆锥容积为

，

．

球取出后，水面下降到，水的体积为

．

又，则，

解得．

答：球取出后，圆锥内水平面高为．

说明：抓住水的何种不变这个关键，本题迅速获解．

典型例题十四

例14 球面上有三点、、组成这个球的一个截面的内接三角形三个顶点，其中，、，球心到这个截面的距离为球半径的一半，求球的表面积．

分析：求球的表面积的关键是求球的半径，本题的条件涉及球的截面，是截面的内接三角形，由此可利用三角形求截面圆的半径，球心到截面的距离为球半径的一半，从而可由关系式求出球半径．

解：∵，，，

∴，是以为斜边的直角三角形．

∴的外接圆的半径为，即截面圆的半径，

又球心到截面的距离为，

∴，得．

∴球的表面积为．

说明：涉及到球的截面的问题，总是使用关系式解题，我们可以通过两个量求第三个量，也可能是抓三个量之间的其它关系，求三个量．例如，过球表面上一点引三条长度相等的弦、、，且两两夹角都为，若球半径为，求弦的长度．由条件可抓住是正四面体，、、、为球上四点，则球心在正四面体中心，设，则截面与球心的距离，过点、、的截面圆半径，所以得．

典型例题十五

例15　、是半径为的球的球面上两点，它们的球面距离为，求过、的平面中，与球心的最大距离是多少？

分析：、是球面上两点，球面距离为，转化为球心角，从而，由关系式，越小，越大，是过、的球的截面圆的半径，所以为圆的直径，最小．

解：∵球面上、两点的球面的距离为．

∴，∴．

当成为圆的直径时，取最小值，此时，取最大值，

，

即球心与过、的截面圆距离最大值为．

说明：利用关系式不仅可以知二求一，而且可以借此分析截面的半径与球心到截面的距离之间的变化规律．此外本题还涉及到球面距离的使用，球面距离直接与两点的球心角有关，而球心角又直接与长度发生联系，这是使用或者求球面距离的一条基本线索，继续看下面的例子．

典型例题十六

例16　正三棱锥的高为1，底面边长为，正三棱锥内有一个球与其四个面相切．求球的表面积与体积．

分析：球与正三棱锥四个面相切，实际上，球是正三棱锥的内切球，球心到正三棱锥的四个面的距离相等，都为球半径．这样求球的半径可转化为球球心到三棱锥面的距离，而点面距离常可以用等体积法解决．

解：如图，球是正三棱锥的内切球，到正三棱锥四个面的距离都是球的半径．

是正三棱锥的高，即．

是边中点，在上，

的边长为，∴．

∴

可以得到．

由等体积法，

∴

得：，

∴．

∴．

说明：球心是决定球的位置关键点，本题利用球心到正三棱锥四个面的距离相等且为球半径来求出，以球心的位置特点来抓球的基本量，这是解决球有关问题常用的方法．比如：四个半径为的球两两外切，其中三个放在桌面上，第四个球放在这三个球之上，则第四个球离开桌面的高度为多少？这里，四个球的球心这间的距离都是，四个球心构成一个棱长为的正四面体，可以计算正四面体的高为，从而上面球离开桌面的高度为．

典型例题十七

例17　求球与它的外切圆柱、外切等边圆锥的体积之比．

分析：首先画出球及它的外切圆柱、等边圆锥，它们公共的轴截面，然后寻找几何体与几何体之间元素的关系．

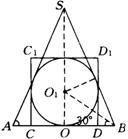
解：如图，等边为圆锥的轴截面，此截面截圆柱得正方形，截球面得球的大圆圆．

设球的半径，则它的外切圆柱的高为，底面半径为；

，

，

∴，，

，

∴．

典型例题十八

例18　正三棱锥的侧棱长为，两侧棱的夹角为，求它的外接球的体积．

分析：求球半径，是解本题的关键．

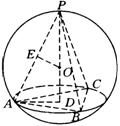
解：如图，作底面于，则为正的中心．

∵底面，∴、、三点共线．

∵，．

∴．

∴，

设，作于，在中，

∵，

又，∴．

在中，∵，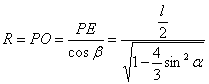

∴．

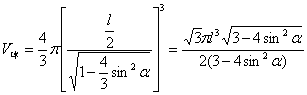说明：解决与球有关的接、切问题时，一般作一个适当的截面，将问题转化为平面问题解决，这类截面通常指圆锥的轴截面、球的大圆、多面体的对角面等，在这个截面中应包括每个几何体的主要元素，且这个截面必须能反映出体和体之间的主要位置关系和数量关系．

典型例题十九

例19 在球心同侧有相距的两个平行截面，它们的面积分别为和．求球的表面积．

分析：可画出球的轴截面，利用球的截面性质，求球的半径．

解：如图为球的轴截面，由球的截面性质知，，且若、分别为两截面圆的圆心，则，．设球的半径为．

∵，∴

同理，∴

设，则．

在中，；在中，，

∴，解得，

∴，∴

∴．

∴球的表面积为．