《直线与平面的垂直的判定、性质》单元测试卷

一、　　　　　　 选择题

1.如果直线和平面内的无数条直线都垂直,那么(　　　)

A.　　　 B.与相交　　　　　　 C.　　　　  D.与的关系不确定

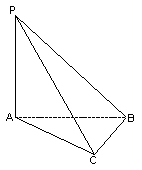2.如图，PA⊥平面ABC，△ABC中，BC⊥AC，则图中直角三角形的个数是（　　　 ）。

A.4　　　 B.3　　　　C.2　　　　D.1

3.两条异面直线在同一平面内的射影是(　　　 ).

A.两条平行直线　　　　　　 B.两条相交直线

C.一个点和一条直线　　　　 D.以上都有可能

4.已知Rt△ABC中，∠C=90°,点P在平面ABC外，且PA=PB=PC,

PO⊥平面ABC于点O，则O是（　　　 ）

A.AC边的中点　　　 B.BC边的中点

C.AB边的中点　　　 D.以上都有可能

5.a,b表示两条直线，表示平面，给出以下命题，其中正确的命题是（　　　 ）

①a⊥,b∥a⊥b　　　　　 ②a⊥, a⊥b b∥

③a∥, a⊥b b⊥　　　　 ④a⊥,b∥ab⊥

A.①②　　　　B.②③　　　　  C.③④　　　　  D.①④

6.已知P是平面四边形ABCD所在平面外一点，且P到这个四边形各边的距离相等，那么这个四边形一定是（　　　 ）。

A.圆内接四边形　　　 B.矩形　　　　C.圆外切四边形　　　 D.平行四边形

7.正方体ABCD-A₁B₁C₁D₁中，E为A₁C₁的中点，则直线CE垂直于（　　 ）。

A.AC　　　  B.BD　　　 C.A₁D₁　　　 D.AA₁

8.下列命题中真命题是（　　　）。

A.和平面的斜线垂直的直线也和这条斜线的射影垂直

B.和斜线的射影垂直的直线也和斜线垂直

C.如果两条直线垂直于同一个平面，那么这两条直线平行

D.和斜线的射影不垂直的直线也和斜线不垂直

9.从平面外一点P作与相交的直线，使得P与交点的距离为1，则满足条件的直线条数一定不可能是（　　　 ）.

A.0　　　　  B.1　　　　  C.2　　　 D.无数个

10.已知PA⊥平面ABCD，四边形ABCD是矩形，并且PA=6,AB=3,AD=4，则P到BD的距离是（　　　）.

A.　　　　　 B.　　　　  C.　　　　　  D.

11. Rt△ABC的斜边AB在平面内，直角顶点C在平面外，C在上的射影为D（不在AB上），则△ABD是（　　　 ）。

A.直角三角形　　　B.锐角三角形　　　 C.钝角三角形　　 D.锐角或钝角三角形

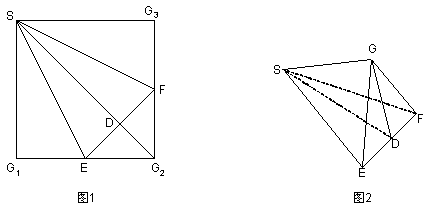
12.如图1，在正方形SG₁G₂G₃中，E,F分别是边G₁G₂,G₂G₃的中点，D是EF的中点，现沿SE,SF及EF把这个正方形折成一个几何体如图2，使G₁,G₂,G₃三点重合于点G，这样，下面结论成立的是（　　　）。

A.SG⊥平面EFG　　　　 B. SD⊥平面EFG

C.FG⊥平面SEF　　　　 D. DG⊥平面SEF

二、　　　　　　 填空题

13.室内有一直尺,无论怎样放置,地面上总有这样的直线与该直尺的边所在的直线__________.

14.在空间四边形ABCD中，如果AB⊥CD，BC⊥DA，那么对角线AC与BD的位置关系是__________。

15.在长为6的线段AB的垂直平分面内有两点C,D,并且AC=5,AD=8,则C,D两点间的最大距离为__________;最小距离为______________.

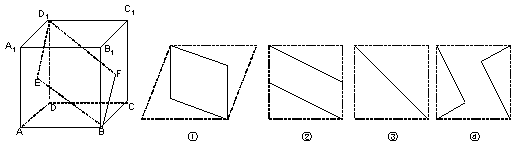
16.如图，E，F分别为正方体的面ADD₁A₁，面BCC₁B₁的中心，则四边形BFD₁E在该正方体的面上的射影可能是__________（要求:把可能的图序号都填上）。

三、　　　　　　 解答题

17. 已知P是△ABC所在平面外一点，PA⊥PB，PB⊥PC，PC⊥PA，H是△ABC的垂心，

　　求证：PH⊥平面ABC。

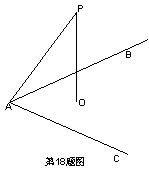
18.如图，∠BAC=90°，点P在平面ABC外，∠PAB=60°，∠PAC=60°，PO⊥平面ABC于O，　　并且PO=a,求线段PA的长。

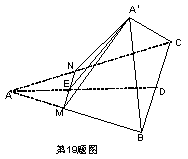
19.如图，AD是△ABC的边CB上的高，E为AD上的点，且，过E作直线MN平行于BC交AB于点M，交AC于点N，将△AMN沿MN折过去，此时A点到了A′的位置，成了一个立体图形，若∠A′ED=60°，求证:EA′⊥平面A′BC。

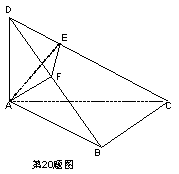
20.如图，在空间四边形ABCD中，DA⊥平面ABC，∠ABC=90°，AE⊥CD，AF⊥DB，

　求证：EF⊥DC。

21.已知等腰Rt△ABC中，∠ACB=90°，AC=2，以AB边上的高CD为折痕，把Rt△ABC对折，对折后∠ADB=90°，求对折后D与D在平面ABC上的射影之间的距离。

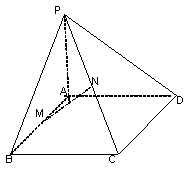22.如图,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.

(1)求证:MN⊥CD;

(2)若∠PDA=45°,求证:MN⊥平面PCD.

参考答案：

1.　　 当与内的无数条平行直线垂直时，和的关系不能确定，故选D。

2.　　　 △PAC, △PAB, △PCB, △ACB都是直角三角形，故选A。

3.　　　 选D。

4.　　　 由PA=PB=PC得OA=OB=OC，∴O是Rt△ABC的外心∴O是AB边的中点。故选C。

5.　　　 对于②，b可能在内；对于③，b可能在内，也可能b∥。故选D。

6.　　　 由题意可知P在平面ABCD内的射影到四边形的各边距离相等，故选C。

7.　　　 连结B₁D₁，由正方体的性质知B₁D₁和BD平行。在正方形A₁B₁C₁D₁中，B₁D₁⊥A₁C₁,又∵CC₁⊥平面A₁C₁，∴CE在平面A₁C₁上的射影为A₁C₁，∴B₁D₁⊥CE且B₁D₁∥BD∴BD⊥CE,故选B。

8.　　　 利用三垂线定理及逆定理要注意条件：直线在平面内。故选C。

9.　　　 设P到平面的距离为d，若d>1，则这样的直线不存在；若d=1，则有1条；若0<d<1，则有无数条。故选C。

10.　 P到BD的距离是,故选A。

11.　 ∵AD<AC,BD<BC∴AD²+DB²<AC²+BC²=AB²∴∠ADB为钝角,故选C.

12.　 在图1中,SG₁⊥G₁E,SG₃⊥G₃F∴在图2中SG⊥GE,SG⊥GF∴SG⊥平面EFG,故选A.

13.　 由三垂线定理易得填垂直。

14.　 过A作AH⊥平面BCD∵CD⊥AB，BC⊥AD∴CD⊥BH，BC⊥DH，故H为△BCD的垂心，连结CH，则BD⊥CH，故BD⊥AC。

15.　 C,D两点间的最大距离为,

最小距离为

16.　 四边形BFD₁E在平面ABCD与平面A₁B₁C₁D₁，面ABB₁A₁与面DCC₁D₁的射影都是②；四边形BFD₁E在面ADD₁A₁与面BCC₁B₁的射影是③，故填②③。

17.　 ∵PA⊥PB，PA⊥PC，PB∩PC=C∴PA⊥平面PBC∴PA⊥BC又∵H是△ABC的垂心∴AH⊥BC∴BC⊥平面PAH∴BC⊥PH，同理可证得AB⊥PH∴PH⊥平面ABC。

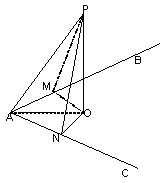
18.　 如图，过O作OM⊥AB于点M，ON⊥AC于点N，

连结AO,PM,PN

∵PO⊥平面ABC∴AB⊥PM,AC⊥PN

∵∠PAB=∠PAC=60°,PA=PA∴Rt△PAM≌Rt△PAN∴PM=PN

∴Rt△POM≌Rt△PON∴OM=ON∴∠MAO=∠MBO

设PA=x,在Rt△PAM中，∠PAM=60°∴AM=

在Rt△AMO中，∠MAO=45°∴AO=

在Rt△PAO中，PA²=AO²+OP²∴∴即

19.∵AD⊥BC,MN∥BC∴MN⊥AD,即MN⊥AE∴MN⊥A′E∴BC⊥A′E

连结A′D，在△A′ED中，设ED=a，则A′E=。又∠A′ED=60°∴∠EA′D=90°,

即A′E⊥A′D∵EA′⊥BC∴EA′⊥平面A′BC

20.∵DA⊥平面ABC∴DA⊥CB∵BC⊥AB∴BC⊥平面ABD∴BC⊥AF∵BD⊥AF∴AF⊥平面BCD∴AF⊥CD∵AE⊥CD∴CD⊥平面AEF∴CD⊥EF.

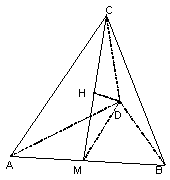21. 取AB的中点M,连结CM,作DH⊥CM于H.

在等腰Rt△ABC中，∠ACB=90°，AC=2∴AD=BD=CD=

∴AB⊥DM∵CD⊥AD,CD⊥BD∴CD⊥平面ABD∴AB⊥CD

∴AB⊥平面MDC∵DH平面MDC∴DH⊥AB

∵DH⊥CM∴DH⊥平面ABC即H为D在平面ABC上的射影

在等腰Rt△ABD中, AD=BD= ∴DM=1,

∵CD=,∠CDM=90°

即

∴D与D在平面ABC上的射影之间的距离为.

22.(1)取AC中点O,连结NO,MO,则NO∥PA.∵PA⊥平面ABCD∴NO⊥平面ABCD

∵MO⊥AB∴MN⊥AB∵CD∥AB∴MN⊥CD.

(2)∵∠PDA=45°∴PA=AD,由△PAM≌△CBM得PM=CM∴MN⊥PC∵MN⊥CD,PC∩CD=C

∴MN⊥平面PCD