典型例题一

例1　求经过两点A(2，1)，B(m，2)(mR)的直线的斜率，并求出其倾斜角及其取值范围．

分析：斜率公式成立的条件是，所以应先就m的值是否等于2进行讨论．

解：当m=2时，

∴直线垂直于轴，故其斜率不存在，此时，倾斜角=．

当m2时，k＝

当m＞2时，＞0　 此时＝arctan（０，）．

当m＜2时，＜0　 此时＝+arctan（，）．

说明：通过讨论确定直线的斜率存在与不存在是解决直线斜率问题常用的方法．

典型例题二

例2　已知两点A(-3，4)，B(3，2)，过点P(2，－1)的直线l与线段AB有公共点．

　　　　（1）求直线l的斜率的取值范围．（2）求直线l的倾斜角的取值范围．

分析：如图1，为使直线l与线段AB有公共点，则直线l的倾斜角应介于直线PB的倾斜角与直线PA的倾斜角之间，所以，当l的倾斜角小于90°时，有；当l的倾斜角大于90°时，则有．

解：如图1，有分析知

　　＝－1，

　　 ＝3．

　　　　∴ （1）或．

　　　　　 （2）arctan3．

说明：学生常错误地写成－1k3，原因是与倾斜角分不清或误以为正切函数在上单调递增．

典型例题三

例3　判断下列命题是否正确：

①一条直线l一定是某个一次函数的图像；

②一次函数的图像一定是一条不过原点的直线；

③如果一条直线上所有点的坐标都是某一个方程的解，那么这个方程叫做这条直线的方程；

④如果以一个二元一次方程的解为坐标的点都在某一条直线上，那么这条直线叫做这个方程的直线．

解：①不正确．直线，不是一次函数；

②不正确．当时，直线过原点．

③不正确．第一、三象限角的平分线上所有的点都是方程的解，但此方程不是第一、三象限角平分线的方程

④不正确．以方程 ()的解为坐标的点都在第一象限的角平分线上，但 此直线不是方程 ()的图像．

说明：直线方程概念中的两个条件缺一不可，它们和在一起构成充要条件．

典型例题四

例4　设直线的斜率为k，且，指出直线倾斜角的范围．

分析：倾斜角与斜率有关，根据公式和正切函数的单调性，由斜率的范围可以得到倾斜角的范围，可以画图，利用数形结合来帮助解决问题．

解： ，由已知得 ．

　　　　，．

　　　　∴ 直线的倾斜角的范围是．

　　说明：注意正切函数在范围的单调性，最好结合图形，不容易出错．

典型例题五

例5　已知两点A(－1，－5)，B(3，－2)，直线l的倾斜角是直线倾斜角的一半，求直线l的斜率．

解1：设直线l的倾斜角为，则直线的倾斜角为2

tan2＝＝，

∴＝．

化简得　3tan²+8tan－3＝0，

解得　tan＝ 或 tan＝－3．

tan2＝＞0，

∴　0°<2<90°，　0°<<45°，

∴　tan＞0，故直线的斜率是．

解2：(思路要点)根据tan2＝＝，且2为锐角，

易得sin2＝和cos2＝，

进一步有：tan＝=．

说明：这里应考虑角的取值范围及函数值的取舍，解２计算更容易．

典型例题六

例6　已知a、b、m都是正数，且，试用解析法证明：>

证明：如图2，

在坐标平面上取点A(m，m)，B(a，b)，

则AB的中点为C(，)．

　　　　显然OA、OB、OC的斜率满足

　　　　　　　　　  ，

　　　　又　，，1．

　　　　所以 >．

说明：本题与前边不等式的证明联系紧密，此处提供了一种新颖的证明，有助于学生对解析法的理解．同时本题为构造性证明，不易想到．事实上，把分式看成斜率是常用的方法．

典型例题七

例7 设直线过原点，其倾斜角为，将直线绕坐标原点沿逆时针方向旋转45°，得到直线，则直线的倾斜角为（　　）．

A．　　　　　　  B．　　　　　　  C．

D．当时为，当时为

分析：倾斜角的范围是，因此，只有当，即时，的倾斜角才是．而，所以必须讨论的情况，结合图形和倾斜角的概念，即可得到时的倾斜角为．故应选D．

答案：D

说明：在求直线的倾斜角时，应该重视的是：(1)注意角的取值范围；(2)数形结合是一种常用而有效的方法．

典型例题八

例8 若三点，，共线，求的值．

分析：若三点共线，则由任两点所确定的直线斜率相等或都不存在．

解答：由、、三点共线，则．

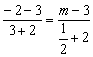∴，解得．

说明：由三点共线求其中参数的方法很多，如两点间的距离公式，定比分点坐标公式，面积公式等，但用斜率公式求的方法最简便．

典型例题九

例9　 (1)直线过点和点，求的斜率和倾斜角；

(2)若直线过，两点，且，求此直线的倾斜角．

(3)已知直线过点和，求的倾斜角和斜率．

分析：(1)中直线上两点与均为已知点，故是确定的，其斜率和倾斜角自然也是确定的，直接利用斜率公式求解即可；(2)中的直线上的点是已知的，点的横纵坐标与角有关，应注意条件中地取值范围；(3)中的直线上的点是已知的，而点的横坐标不确定，它的取值将影响直线的斜率及倾斜角，应对类讨论，以直线的斜率是否存在为分类的标准．根据倾斜角和斜率的概念进行求解．

解：设直线的斜率为，倾斜角为．

(1)∵直线过点和点，

∴它的斜率．

于是．

∵，，

∴的倾斜角，

即：．

(2)因为，所以．所以斜率：

．

因为，所以．

所以，直线的倾斜角为．

(3)当时，直线与轴垂直．所以，倾斜角，没有斜率．

当时，斜率．

若，则；

若，则．

因此，当时，，直线没有斜率．

当时，，．

当时，，．

说明：由斜率求倾斜角时，要注意倾斜角的取值范围是．当倾斜角不是特殊角而必须用反正切表示时，应注意．

(1)当直线的倾斜角是时，斜率是．但反过来，当直线的斜率是时，直线的倾斜角不一定是．

(2)在用公式时，要注意两点：

①斜率公式与两点的顺序无关，即两点的纵坐标和横坐标在公式中的次序可以同时颠倒．

②当，（即直线和轴垂直）时，不能用此公式，此时倾斜角是，直线没有斜率．

(3)解答本题易出错的地方是对参数未进行讨论或讨论不完整．