典型例题一

例1　今有标号为1、2、3、4、5的五封信，另有同样标号的五个信封，现将五封信任意地装入五个信封中，每个信封一封信，试求至少有两封信与信封标号一致的概率．

　　分析：至少有两封信与信封的标号配对，包含了下面两种类型：两封信与信封标号配对；3封信与信封标号配对；4封信与信封标号配对，注意：4封信配对与5封信配对是同一类型．现在我们把上述三种类型依次记为事件，可以看出两两互斥，记“至少有两封信与信封标号配对”为事件，事件发生相当于有一个发生，所以用公式可以计算.

　　解：设至少有两封信配对为事件，恰好有两封信配对为事件，恰有3封信配对为事件，恰有4封信（也就是5封信）配对为事件，则事件等于事件，且事件为两两互斥事件，所以．

　　5封信放入5个不同信封的所有放法种数为，

　　其中正好有2封信配对的不同结果总数为

　  正好有3封信配对的不同结果总数为

　　正好有4封信（5封信）全配对的不同结果总数为1，

　　而且出现各种结果的可能性相同，

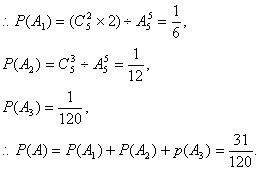
　　说明：至少有两封信与信封配对的反面是全不配对和恰好有1封信配对，但是配对越少，计算该结果的所有方法总数越困难，即计算该事件的概率越不方便．现在把问题改为计算“至多两封信与信封标号配对”的概率是多少？我们转化为求其对立事件的概率就简单得多，它的对立事件为“3封信配对或4封信（即5封）配对”，得到其结果的概率为，在计算事件的概率时有时采用“正难则反”的逆向思维方法，直接计算事件的概率比较难，而计算其对立事件的概率比较容易时可采用这种方法．

典型例题七

例7　射手张强在一次射击中射中10环、9环、8环、7环、7环以下的概率分别为，，，，．计算这个射手在一次射击中：

(1)射中10环或9环的概率；

(2)至少射中7环的概率；

(3)射中环数不足8环的概率．

分析：“射中10环”，“射中9环”，…“射中7环以下”是彼此互斥事件，可运用“事件的和”的概率公式求解．

解：设“射中10环”、“射中9环”、“射中8环”、“射中7环”、“射中7环以下”的事件分别为、、、、，则

(1)，

所以射中10环或9环的概率为．

(2)

，

所以至少射中7环的概率为．

(3) ，

所以射中环数不足8环的概率为．

说明：公式只有在、两事件互斥时才使用，如果、两事件不互斥，就不能应用这一公式，一定要注意这一公式应用的前提是、两个事件互斥．

典型例题三

例3　有4个红球，3个黄球，3个白球装在袋中，小球的形状、大小相同，从中任取两个小球，求取出两个同色球的概率是多少？

　　分析：与倒2中取球方式不同的是，从中取出两球是不放回的取出．处理上，例2是分步取球，先取哪个后取哪个是有区别地对待，而本例中，只要搞清是取的什么球，直接用组合数列式．取出两个同色球可以分成下面几个类型：两个红球；两个黄球；两个白球．

　　解：从10个小球中取出两个小球的不同取法数为

　　“从中取出两个红球”的不同取法数为，其概率为

　　“从中取出两个黄球”的不同取法数为，其概率为

　　“从中取出两个白球”的不同取法数为，其概率为

　　所以取出两个同色球的概率为：

　　说明：本题求取出两个同色球的概率，对结果比较容易分类，如果换上“取出3个球，至少两个同颜色”，这样的问题分类相对就比较复杂，在此我们不一一列出，但考虑其反面，对立事件为“取出3个球，颜色全不相同”，对立事件的概率比较容易算出．取出3个球，颜色全不相同的所有不同取法数为（种），对立事件的概率为，所以“取出3个球，至少两个同颜色”的概率为：

典型例题九

例9　小明的袋中放有3个伍分硬币、3个贰分硬币和4个壹分硬币，从中任取3个，求总数超过8分的概率．

分析1：视其为互斥事件，进而求概率．

解法1：(1)记“总数超过8分”为事件，它包括下列四种情况：①“取到3个伍分硬币”记为事件；②“取到2个伍分硬币和1个贰分硬币”为事件；③“取到2个伍分硬币和1个壹分硬币”为事件；④“取到１个伍分硬币和2个贰分硬币”为事件．

，，

，．

根据题意，、、、彼此互斥，故所求概率

．

分析2：视其为等可能事件，进而求概率．

解法2：从10个硬币中取3个，共有种不同方法．“总数超过8分”的共有以下四种情况：①取3个伍分硬币，共有种方法；②取2个伍分硬币和1个贰分硬币，共有种方法；③取2个伍分硬币和1个壹分硬币，共有种方法；④取１个伍分硬币和2个贰分硬币，共有种不同方法，所以“总数超过8分”共有种方法．∴总数超过8分的概率为．

说明：复杂的等可能事件的概率可化为彼此互斥的简单事件来求，要注意分类的不重、不漏．

典型例题二

例2　袋中装有红、黄、白3种颜色的球各1只，从中每次任取1只，有放回地抽取3次，求：

　　（1） 3只全是红球的概率，（2） 3只颜色全相同的概率，

　　（3） 3只颜色不全相同的概率，（4） 3只颜色全不相同的概率．

　　分析：有放回地抽3次的所有不同结果总数为，3只全是红球是其中的1种结果，同样3只颜色全相同是其中3种结果，全红、全黄、全白，用求等可能事件的概率方式可以求它们的概率．“3种颜色不全相同”包含的类型较多，而其对立事件为“三种颜色全相同”却比较简单，所以用对立事件的概率方式求解．3只颜色全不相同，由于是一只一只地按步取出，相当于三种颜色的一个全排列，其所有不同结果的总数为，用等可能事件的概率公式求解．

　　解：有放回地抽取3次，所有不同的抽取结果总数为：

　　3只全是红球的概率为

　　3只颜色全相同的概率为

　　“3只颜色不全相同”的对立事件为“三只颜色全相同”．

　　故“3只颜色不全相同”的概率为

　　“3只颜色全不相同”的概率为

　　说明：如果3种小球的数目不是各1个，而是红球3个，黄球和白球各两个，其结果又分别如何？首先抽3次的所有不同结果总数为，全是红球的结果总数为，所以全是红球的概率为，同样全是黄球的概率为，全是白球的概率也是，所以3只球颜色全相同的概率为上述三个事件的概率之和，，“三种颜色不全相同”为“三种颜色全相同”的对立事件，其概率为 “3只小球颜色全不相同”可以理解为三种颜色的小球各取一只，然后再将它们排成一列，得到抽取的一种结果，其所有不同结果总数为（种），所以“3只小球颜色全不相同”的概率为

典型例题五

例5　判断下列各对事件是否是互斥事件，并说明道理．

某小组有3名男生和2名女生，从中任选2名同学去参加演讲比赛，其中

(1)恰有1名男生和恰有2名男生；

(2)至少有一名男生和至少有一名女生；

(3)至少有一名男生和全是男生；

(4)至少有1名男生和全是女生．

分析：判断两个事物是否为互斥事件，就是考察它们能否同时发生，如果不能同时发生，则是五斥事件，不然就不是互斥事件．

解：(1)是互斥事件

道理是：在所选的2名同学中，“恰有1名男生”实质是选出的是“一名男生和一名女生”，它与“恰有两名男生”，不可能同时发生，所以是一对互斥事件．

(2)不可能是互斥事件

道理是：“至少有1名男生”包括“1名男生、1名女生”和“两名都是男生”两种结果．“至少有1名女生”包括“1名女生、1名男性”和“两名都是女生”两种结果，它们可同时发生．

(3)不可能是互斥事件

道理是：“至少有一名男生”包括“一名男生、一名女生”和“两名都是男性”，这与“全是男生”，可同时发生．

(4)是互斥事件

道理是：“至少有1名男生”包括“1名男生、1名女生”和“两名都是男生”两种结果，它和“全是女生”不可能同时发生．

小结：互斥事件是概率知识中重要概念，必须正确理解．

(1)互斥事件是对两个事件而言的．若有、两个事件，当事件发生时，事件就不发生；当事件发生时，事件就不发生（即事件、不可能同时发生），我们就把这种不可能同时发生的两个事件叫做互斥事件．否则就不是互斥事件．

(2)对互斥事件的理解，也可以从集合的角度去加以认识．

如果、是两个互斥事件，反映在集合上，是表示、这两个事件所含结果组成的集合彼此互不相交．

如果事件中的任何两个都是互斥事件，那么称事件彼此互斥，反映在集合上，表现为由各个事件所含的结果组成的集合彼此互不相交．

典型例题八

例8　玻璃球盒中装有各色球12只，其中5红、4黑、2白、1绿，求从中取1球：(1)红或黑的概率；(2)红或黑或白的概率．

分析1：视其为等可能事件，进而求概率．

解法1：(1)从12只球中任取1球得红球有5种取法，得黑球有4种取法，得红球或黑球共有种不同取法，任取一球有种取法，

∴任取1球得红球或黑球的概率得．

(2)从12只球中任取1球得红球有5种取法，得黑球有4种方法，得白球有2种取法，从而得红或黑或白球的概率为．

分析2：视其为互斥事件，进而求概率．

解法2：记事件：从12只球中任取1球得红球；：从中任取1球得黑球；：从中任取1球得白球；：从中任取1球得绿球，则

，，，．

根据题意，、、、彼此互斥，由互斥事件概率得．

(1)取出红球或黑球的概率为

；

(2)取出红或黑或白球的概率为

．

分析3：应用对立事件求概率．

解法3：(1)由思路2，取出红球或黑球的对立事件为取出白球或绿球，即的对立事件为，

∴取出红球或黑球的概率为

．

(2)的对立事件为．

即为所求．

说明：(1)“互斥”和“对立”事件容易搞混．互斥事件是指指事件不能同时发生，对立事件是指互斥的两事件中必有一个发生．

(2)求复杂事件的概率通常有两种方法：一是将所求事件转化成彼此互斥的事件的和；二是先去求对立事件的概率，进而再求所求事件的概率．

典型例题六

例6　判断下列给出的每对事件，(1)是否为互斥事件，(2)是否为对立事件，并说明道理．

从扑克40张(红桃、黑桃、方块、梅花点数从1—10各10张)中，任取一张．

(1)“抽出红桃”与“抽出黑桃”；

(2)“抽出红色牌”与 “抽出黑色色牌”；

(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”．

解：(1)是互斥事件，不是对立事件．

道理是：从40张扑克牌中任意抽取1张，“抽出红桃”和“抽出黑桃”是不可能同时发生的，所以是互斥事件，同时，不能保证其中必有一个发生，这是由于还可能抽出“方块”或者“梅花”，因此，二者不是对立事件．

(2)既是互斥事件，又是对立事件．

道理是：从40张扑克牌中，任意抽取1张．“抽出红色牌”与“抽出黑色色牌”，两个事件不可能同时发生，但其中必有一个发生，所以它们既是互斥事件，又是对立事件．

(3)不是互斥事件，当然不可能是对立事件

道理是：从40张扑克牌中任意抽取1张．“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”这两个事件可能同时发生，如抽得10，因此，二者不是互斥事件，当然不可能是对立事件．

说明：“互斥事件”和“对立事件”都是就两个事件而言的，互斥事件是不可同时发生的两个事件，而对立事件是其中必有一个发生的互斥事件．因此，对立事件必须是互斥事件，但互斥事件不一定是对立事件，也就是说“互斥事件”是“对立事件”的必要但不充分的条件．“对立事件”是“互斥事件”的充分不必要条件．

典型例题十

例10　同时抛掷两枚骰子，求至少有一个5点或6点的概率．

分析1：视其为等可能事件，进而求概率．

解法1：同时投掷两枚骰子，可能结果如下表：

共有36个不同的结果，其中至少有一个5点或6点的结果有20个，所以至少有一个5点或6点的概率为．

分析2：利用对立事件求概率．

解法2：至少有一个5点或6点的对立事件是没有5点或6点．如上表，没有5点或6点的结果共有16个，没有5点或6点的概率为．

至少有一个5点或6点的概率为．

下面再给出一种解法（此解法可在下一节学完后，再学习）

分析3：利用公式．

解法3：记事件：含有点数为5的．

事件：含有点数为6的．显然、不是互斥事件

，，

∴至少有一个5点或6点的概率为

．

说明：(1)本题常出现的错误有两类：一类是不符合题意的臆想，含5的有6个，含6的有6个，∴至少有一个5或6的有12个，从而所求概率为；另一类是没有搞清楚、是否为互斥事件，直接利用公式．

(2)解题时，将所有基本事件全部列出是避免重复和遗漏的有效方法；对于用直接法难于解决的问题，可求其对立事件的概率，进而求得概率，以降低难度．

典型例题十一

例11 一批产品共件，其中件是废品，任抽件进行检查，求下列事件的概率．

(1)件产品中至多有一件废品；

(2)件产品中至少有一件废品．

分析：件产品中恰有件废品是互斥事件，可用概率加法公式．

解：设为事件“件产品中恰有件废品”，其中，易知()为彼此互斥事件．

(1)设为事件“件产品中至多有件废品”，则有，又由于与互斥，所以

(2)(法1)设为事件“件产品中至少有件废品”，则有，而且彼此互斥，所以

 

 

(法2)由于的对立事件为“件产品中无废品”，即，

∴

．

说明：抽查产品问题与模球问题类似，是一类典型问题，应予以很好地理解和掌握．(1)“至多有一件废品”的意义是“可以有一件废品，也可以没有废品”，即（又，∴），其反面是“有件以上废品”，即（故）．“至少有一件废品”的意义是“可以一件废品、可以有两件废品，…，可以有五件废品”，即，（故），其反面是“没有废品”，即（故）．要正确理解“至多”、“至少”的含义，有时直接解简单，而有时用其反而去解简单．(2)注意求概率的直接法和间接法两种思路．

典型例题十三

例13 学校文娱队员唱歌、跳舞至少会一项，已知会唱歌的有人，会跳舞的有人，现从中选人，且至少有一位既会唱歌又会跳舞的概率是，问该文娱队有多少人？

分析：可选设既会唱歌又会跳舞的人数为，则该队的队员人数为人．如图所示．

解：设该队既会唱歌又会跳舞的人有名，则该队队员的人数为名，只会唱歌的人有人，只会跳舞的人有人，从中选出人，记为事件“至少有一位既会唱歌又会跳舞的人”，则的对立事件为“人都只会唱歌或只会跳舞”．

∵，

∴．

∴．

解得：．

∴．

∴该文娱队共有人．

说明：(1)注意集合元素个数的计算方法：card（）=card+card-card（）．(2)本题中出现了“至少”一词，可考虑从反而做，因为人数不知，所以从正面做较繁．

典型例题十二

例12 某战士射击一次，设中靶的概率为．令事件为“射击一次、中靶”，求：

(1)的概率是多少？

(2)若事件（中靶环数大于）的概率是，那么事件（中靶环数小于）的概率是多少？事件（中靶环数大于且小于）的概率是多少？

分析：(1)易做．(2)搞清三个事件、、之间的包含或对立关系．

解：(1) ．

(2)由题意，事件即为“中靶环数为环”，而事件为“中靶环数为环”，事件为“中靶环数为环”．可见与是对立事件，而．

∴．

又，

∴．

说明：离散型随机变量在某一范围内取值的概率，往往利用其在不同范围内发生的互斥性，再根据概率的加法处理．例如教材中例题：某地区年降水量在(mm)内的概率是，在(mm)内的概率是，则该地区年降水量在(mm)内的概率即为，因为这两个事件是互斥的．

典型例题四

例4　在 9个国家乒乓球队中有 3个亚洲国家队，抽签分成三组进行比赛预赛．求：

　　（1）三个组各有一支亚洲队的概率；（2）至少有两个亚洲国家队在同～组的概率．

　　分析：9个队平均分成三组的所有不同的分法总数为，其中每个队有一支亚洲国家队的分法数为，用等可能事件的概率公式可求其概率．至少有两支亚洲国家队在同一小组可分成两类：恰好有两支亚洲国家队在同一组；三支亚洲国家队在同一组．分别计算它们的概率然后相加．此外，我们也可以先计算其对立事件的概率，而其对立事件为“3支亚洲国家队不在同一组”，实际上两小题的事件互为对立事件．

解：（1）所有的分组结果是等可能的，9支队平均分成3组的不同分法数为：

（种）．

其中三个组各有一支亚洲队，可以看成其它6支队中任取2支队与第1个亚洲队合为一组，剩下4支队任取2支与第2个亚洲队一组，最后2支队与第2、3支亚洲队一组，所有不同的分法数为（种）。

所以“三个组各有一支亚洲队的概率为

（2）方法1：“至少有两支亚洲队在同一组”分为两类：

“恰好两支亚洲国家队在一组”，概率为

“三支亚洲国家队在同一组”的概率为

方法2：“至少有两支亚洲在同一组”的对立事件为“三个组各有一支亚洲队”。

由（1）可得，“至少有两支亚洲队在同一组”的概率为：