典型例题一

例1　讨论表示何种圆锥曲线，它们有何共同特征．

分析：由于，，则的取值范围为，，，分别进行讨论．

解：（1）当时，，，所给方程表示椭圆，此时，，，这些椭圆有共同的焦点（－4，0），（4，0）．

（2）当时，，，所给方程表示双曲线，此时，，，，这些双曲线也有共同的焦点（－4，0），）（4，0）．

（3），，时，所给方程没有轨迹．

说明：将具有共同焦点的一系列圆锥曲线，称为同焦点圆锥曲线系，不妨取一些值，画出其图形，体会一下几何图形所带给人们的美感．

典型例题二

例2　根据下列条件，求双曲线的标准方程．

（1）过点，且焦点在坐标轴上．

（2），经过点（－5，2），焦点在轴上．

（3）与双曲线有相同焦点，且经过点

解：（1）设双曲线方程为

∵ 、两点在双曲线上，

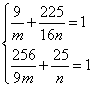∴解得

∴所求双曲线方程为

说明：采取以上“巧设”可以避免分两种情况讨论，得“巧求”的目的．

（2）∵焦点在轴上，，

∴设所求双曲线方程为：（其中）

∵双曲线经过点（－5，2），∴

∴或（舍去）

∴所求双曲线方程是

说明：以上简单易行的方法给我们以明快、简捷的感觉．

（3）设所求双曲线方程为：

∵双曲线过点，∴

∴或（舍）

∴所求双曲线方程为

说明：（1）注意到了与双曲线有公共焦点的双曲线系方程为后，便有了以上巧妙的设法．

（2）寻找一种简捷的方法，须有牢固的基础和一定的变通能力，这也是在我们教学中应该注重的一个重要方面．

典型例题三

例3 已知双曲线的右焦点分别为、，点在双曲线上的左支上且，求的大小．

分析：一般地，求一个角的大小，通常要解这个角所在的三角形．

解：∵点在双曲线的左支上

∴

∴

∴

∵

∴

说明：（1）巧妙地将双曲线的定义应用于解题当中，使问题得以简单化．

（2）题目的“点在双曲线的左支上”这个条件非常关键，应引起我们的重视，若将这一条件改为“点在双曲线上”结论如何改变呢？请读者试探索．

典型例题四

例4 已知、是双曲线的两个焦点，点在双曲线上且满足，求的面积．

分析：利用双曲线的定义及中的勾股定理可求的面积．

解：∵为双曲线上的一个点且、为焦点．

∴,

∵

∴在中，

∵

∴

∴

∴

说明：双曲线定义的应用在解题中起了关键性的作用．

典型例题五

例5　已知两点、，求与它们的距离差的绝对值是6的点的轨迹．

分析：问题的条件符合双曲线的定义，可利用双曲线定义直接求出动点轨迹．

解：根据双曲线定义，可知所求点的轨迹是双曲线．

∵，

∴

∴所求方程为动点的轨迹方程，且轨迹是双曲线．

说明：（1）若清楚了轨迹类型，则用定义直接求出其轨迹方程可避免用坐标法所带来的繁琐运算．

（2）如遇到动点到两个定点距离之差的问题，一般可采用定义去解．

典型例题六

例6　在中，，且，求点的轨迹．

分析：要求点的轨迹，需借助其轨迹方程，这就要涉及建立坐标系问题，如何建系呢？

解：以所在直线为轴，线段的中垂线为轴建立平面直角坐标系，则，．

设，由及正弦定理可得：

∵

∴点在以、为焦点的双曲线右支上设双曲线方程为：

∴，

∴，

∴

∴所求双曲线方程为

∵

∴

∴点的轨迹是双曲线的一支上挖去了顶点的部分

典型例题七

例7　求下列动圆圆心的轨迹方程：

（1）与⊙内切，且过点

（2）与⊙和⊙都外切．

（3）与⊙外切，且与⊙内切．

分析：这是圆与圆相切的问题，解题时要抓住关键点，即圆心与切点和关键线段，即半径与圆心距离．如果相切的⊙、⊙的半径为、且，则当它们外切时，；当它们内切时，．解题中要注意灵活运用双曲线的定义求出轨迹方程．

解：设动圆的半径为

（1）∵⊙与⊙内切，点在⊙外

∴，，

∴点的轨迹是以、为焦点的双曲线的左支，且有：

，，

∴双曲线方程为

（2）∵⊙与⊙、⊙都外切

∴，，

∴点的轨迹是以、为焦点的双曲线的上支，且有：

，，

∴所求的双曲线的方程为：

（3）∵⊙与⊙外切，且与⊙内切

∴，，

∴点的轨迹是以、为焦点的双曲线的右支，且有：

，，

∴所求双曲线方程为：

说明：（1）“定义法”求动点轨迹是解析几何中解决点轨迹问题常用而重要的方法．

（2）巧妙地应用“定义法”可使运算量大大减小，提高了解题的速度与质量．

（3）通过以上题目的分析，我们体会到了，灵活准确地选择适当的方法解决问题是我们无休止的追求目标．

典型例题八

例8　在周长为48的直角三角形中，，，求以、为焦点，且过点的双曲线方程．

分析：首先应建立适当的坐标系．由于、为焦点，所以如图建立直角坐标系，可知双曲线方程为标准方程．由双曲线定义可知，，所以利用条件确定的边长是关键．

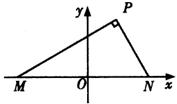
解：∵的周长为48，且，

∴设，，则．

由，得．

∴，，．

以所在直线为轴，以∴的中点为原点建立直角坐标系，设所求双曲线方程为．

由，得，，．

由，得，．

由，得所求双曲线方程为．

说明：坐标系的选取不同，则又曲线的方程不同，但双曲线的形状不会变．解题中，注意合理选取坐标系，这样能使求曲线的方程更简捷．

典型例题九

例9　是双曲线上一点，、是双曲线的两个焦点，且，求的值．

分析：利用双曲线的定义求解．

解：在双曲线中，，，故．

由是双曲线上一点，得．

∴或．

又，得．

说明：本题容易忽视这一条件，而得出错误的结论或．

典型例题十

例10　若椭圆和双曲线有相同的焦点和，而是这两条曲线的一个交点，则的值是(　　) ．

A．　　B．　　C．　　D．

分析：椭圆和双曲线有共同焦点，在椭圆上又在双曲线上，可根据定义得到和的关系式，再变形得结果．

解：因为在椭圆上，所以．

又在双曲线上，所以．

两式平方相减，得，故．选(A)．

说明：(1)本题的方法是根据定义找与的关系．(2)注意方程的形式，，是，，是．

典型例题十一

例11 若一个动点到两个定点、的距离之差的绝对值为定值，讨论点的轨迹．

分析：本题的关键在于讨论．因，讨论的依据是以0和2为分界点，应讨论以下四种情况：，，，．

解：．

(1)当时，轨迹是线段的垂直平分线，即轴，方程为．

(2)当时，轨迹是以、为焦点的双曲线，其方程为．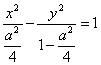

(3)当时，轨迹是两条射线或．

(4)当时无轨迹．

说明：

(1)本题容易出现的失误是对参变量的取值范围划分不准确，而造成讨论不全面．

(2)轨迹和轨迹方程是不同的，轨迹是图形，因此应指出所求轨迹是何种曲线．

典型例题十二

例12　如图，圆与轴的两个交点分别为、，以、为焦点，坐标轴为对称轴的双曲线与圆在轴左方的交点分别为、，当梯形的周长最大时，求此双曲线的方程．

分析：求双曲线的方程，即需确定、的值，而，又，所以只需确定其中的一个量．由双曲线定义，又为直角三角形，故只需在梯形的周长最大时，确定的值即可．

解：设双曲线的方程为()，(，)，()．

连结，则．

作于，则有．

∴，即．

∴梯形的周长

即．

当时，最大．

此时，，．

又在双曲线的上支上，且、分别为上、下两焦点，

∴，即．

∴，即．

∴．

∴所求双曲线方程为．

说明：解答本题易忽视的取值范围，应引起注意．

典型例题十三

例13　、、是我方三个炮兵阵地，和正东6千米，在正北偏西30°，相距4千米，为敌炮阵地，某时刻处发现敌炮阵地的某种信号，由于、两地比距地远，因此后，、才同时发现这一信号，此信号的传播速度为1，若炮击地，求炮击的方位角．

分析：点到、距离相等，因此点在线段的垂直平分线上．又，因此在以、为焦点的双曲线的右支上．由交轨法可求的坐标，进而求炮击的方位角．

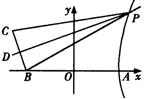
解：如图，以直线为轴，线段的中垂线为轴建立坐标系，则

、、．

因为，所以点在线段的垂直平分线上．

因为，中点，所以直线

．　　　　①

又，故在以、为焦点的双曲线右支上．

设，则双曲线方程为．　②

联立①、②式，得，所以．因此

．

故炮击的方位角为北偏东．

说明：空间物体的定位，一般先利用声音传播的时间差建立双曲线方程，然后借助曲线的交轨来确定．这是解析几何的一个重要应用．