（数学选修1-1）第一章  导数及其应用 [提高训练C组]及答案

一、选择题

1．若,则等于（　　）

A．　 　　　B．　　 C．　　　　　　D．

2．若函数的图象的顶点在第四象限，则函数的图象是（　 ）

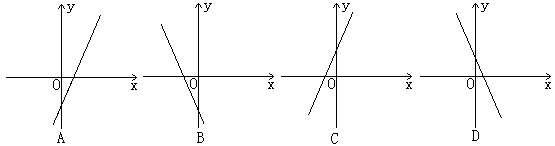3．已知函数在上是单调函数,则实数的

取值范围是（　　）

A．　B．　

C．　D．

4．对于上可导的任意函数，若满足，则必有（　　 ）

A． 　 B.

C. 　　D.

5．若曲线的一条切线与直线垂直，则的方程为（　 ）

A．　 B．　C．　　D．

6．函数的定义域为开区间，导函数在内的图象如图所示，

则函数在开区间内有极小值点（　）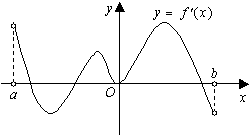

A．个　　B．个　 C．个　　D．个

二、填空题

1．若函数在处有极大值，则常数的值为_________；

2．函数的单调增区间为　　　　　　 。

3．设函数，若为奇函数，则=__________

4．设，当时，恒成立，则实数的

取值范围为　　　　　　 。

5．对正整数，设曲线在处的切线与轴交点的纵坐标为，则

数列的前项和的公式是　　

三、解答题

1．求函数的导数。

2．求函数的值域。

3．已知函数在与时都取得极值

(1)求的值与函数的单调区间

(2)若对，不等式恒成立，求的取值范围。

4．已知,，是否存在实数,使同时满足下列两个条件：（1）在上是减函数，在上是增函数；（2）的最小值是，若存在，求出，若不存在，说明理由.

（数学选修1-1）第一章　导数及其应用　[提高训练C组]

一、选择题

1．A　

2．A　 对称轴，直线过第一、三、四象限

3．B  在恒成立，

4．C　当时，，函数在上是增函数；当时，，在上是减函数，故当时取得最小值，即有

得

5．A　 与直线垂直的直线为，即在某一点的导数为，而，所以在处导数为，此点的切线为

6．A　 极小值点应有先减后增的特点，即

二、填空题

1．　 ，时取极小值

2．　 对于任何实数都成立

3．　　

　　　　 

要使为奇函数，需且仅需，

即：。又，所以只能取，从而。

4．　时，

5．　　 ，

令，求出切线与轴交点的纵坐标为，所以，则数列的前项和

三、解答题

1．解：

。

2．解：函数的定义域为，

当时，，即是函数的递增区间，当时，

所以值域为。

3．解：（1）

由，得

，函数的单调区间如下表：

	­	极大值	¯	极小值	­

所以函数的递增区间是与,递减区间是；

（2），当时，

为极大值，而，则为最大值，要使

恒成立，则只需要，得。

4．解：设

∵在上是减函数，在上是增函数

∴在上是减函数，在上是增函数.

∴　　∴　 解得

经检验，时，满足题设的两个条件.