高二理科数学下学期检测卷()
姓名 班级 成绩
一、选择题(5×12)
1. 已知命题:“直线a上的两个点A,B在平面α内。”与它不等价的命题是
A.直线a在平面α内 B.平面α通过直线
C.直线a上只有两点在平面α内 D.直线a上的所有点都在平面α内
2. 平面![]() 平面
平面![]() 的一个充分条件是
的一个充分条件是
A.存在一条直线![]()
![]() ∥
∥![]() ∥
∥![]() B.存在一条直线
B.存在一条直线![]()
C.存在两条平行直线![]()
D.存在两条异面直线![]() ∥
∥![]() ∥
∥![]()
 3. 已知
3. 已知![]()
A.90° B.30° C.60° D.150°
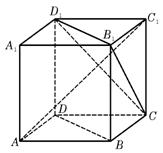
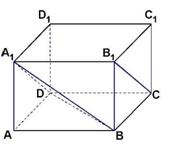
4. 如图,ABCD-A1B
A.BD∥平面CB1D1 B.AC1⊥BD
C.AC1⊥平面CB1D1 D.异面直线AD与CB1角为60°
5. 已知![]() ,
,![]() 为两条不同的直线,
为两条不同的直线,![]() ,
,![]() 为两个不同的平面,
为两个不同的平面,
则下列命题中正确的是A.![]() B.
B. ![]() C.
C.![]() D.
D. ![]()
6. 正方体ABCD-A1B
A.1 B.![]() C.
C.![]() D.
D.![]()
7. 若P是两条异面直线![]() 外的任意一点,则
外的任意一点,则
A.过点P有且仅有一条直线与![]() 都平行 B.过点P有且仅有一条直线与
都平行 B.过点P有且仅有一条直线与![]() 都垂直
都垂直
C.过点P有且仅有一条直线与![]() 都相交 D.过点P有且仅有一条直线与
都相交 D.过点P有且仅有一条直线与![]() 都异面
都异面
8. 平面![]() 外有两条直线
外有两条直线![]() 和
和![]() ,如果
,如果![]() 和
和![]() 在平面
在平面![]() 内的射影分别是
内的射影分别是![]() 和
和![]() ,给出下列四个命题:
,给出下列四个命题:
①![]() ⊥
⊥![]()
![]()
![]() ⊥
⊥![]() ; ②
; ②![]() ⊥
⊥![]()
![]()
![]() ⊥
⊥![]() ;③
;③![]() 与
与![]() 相交
相交![]()
![]() 与
与![]() 相交或重合; ④
相交或重合; ④![]() 与
与![]() 平行
平行![]()
![]() 与
与![]() 平行或重合;其中不正确的命题个数是A.1
B.2
C.3
D.4
平行或重合;其中不正确的命题个数是A.1
B.2
C.3
D.4
9. 若一个长方体共点的三个表面的对角线长分别为a、b、c ,则长方体的对角线长是
 A.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
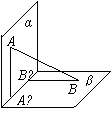
10. 如图,平面α⊥平面β,A∈α,B∈β,
AB与两平面α、β所成的角分别为和,过A、B分别作两平
面交线的垂线,垂足为A′、B′,则AB∶![]() =
=
A.2∶1 B.3∶1
C.3∶2 D.4∶3
11. 已知二面角![]() 的大小为
的大小为![]() ,
,![]() 为异面直线,且
为异面直线,且![]() ,则
,则![]() 所成的角为
所成的角为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
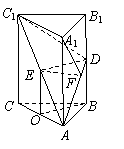
12. 在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是
C. 平面PDF⊥平面ABC D. 平面PAE⊥平面 ABC
二.填空题(5×4)
13. 在三棱锥哦O-ABC中,三条棱![]() 两两互相垂直,且OA=OB=OC=
两两互相垂直,且OA=OB=OC=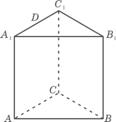 2,M是
2,M是![]() 边的中点,则M到平面OBC的距离是________________
边的中点,则M到平面OBC的距离是________________
14. 如图,已知正三棱柱ABC-A1B
直线AD 与平面B1DC所成角的正弦值为 .
15. 边长为2的正方形ABCD在平面α内的射影是EFCD,如果AC与平面α所成角的大小是![]() ,则AB与平面α的距离为
。
,则AB与平面α的距离为
。
16. 在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体
是 (写出所有正确结论的编号)。①矩形;②不是矩形的平行四边形;③有三个面为等
腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三
角形的四面体。
 2008年宣威八中
2008年宣威八中
高二数学(理科)检测卷
答题卡
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(每小题5分,共20分)
13题 14题
1 5题 16题
三、解答题(共6小题,共计70分)
17、(10分)在长方体![]() 中,已知
中,已知![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成角的大小(结果用反三角函数值表示).
所成角的大小(结果用反三角函数值表示).
18、(12分)如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,且PA=AD=AB=2BC,M、N分别为PC、PB的中点.
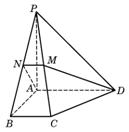 (1)求证:PB⊥DM;
(1)求证:PB⊥DM;
(2)求CD与平面ADMN所成的角。
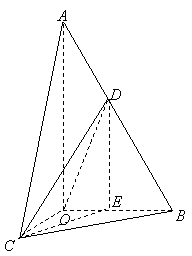
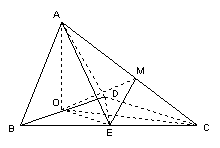
19、(12分)如图,四面体ABCD中,O、E分别是BD、BC的中点,![]()
(1)求证:![]() 平面BCD;
平面BCD;
(2)求点E到平面ACD的距离。
 |
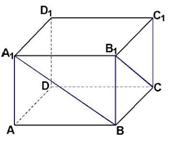
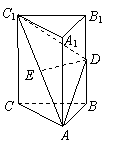
20、(12分)如图,在直三棱柱ABC-A1B
(1)证明:ED为异面直线BB1与AC1的公垂线;
(2)设AA1=AC=AB,求二面角A1-AD-C1的大小.
 |
21、(12分)如图,在![]() 中,
中,![]() ,斜边
,斜边![]() .
.![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角.动点
是直二面角.动点![]() 的斜边
的斜边![]() 上.
上.
(1)求证:平面![]() 平面
平面![]() ;
;
 (2)求
(2)求![]() 与平面
与平面![]() 所成角的最大值
所成角的最大值
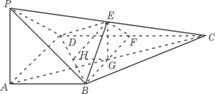
22、(12分)如图,在四棱锥P-ABCD中,PA![]() 底面ABCD,
底面ABCD,![]() DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(1)试证:CD![]() 平面BEF;
平面BEF;
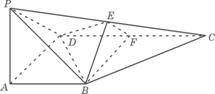 (2)设PA=k·AB,且二面角E-BD-C的平面角大于
(2)设PA=k·AB,且二面角E-BD-C的平面角大于![]() ,求k的取值范围.
,求k的取值范围.
2008年宣威八中
高二数学(理科)检测卷参考答案
一、选择题(每小题5分,共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | D | D | D | D | C | B | D | B | A | B | C |
二、填空题(每小题5分,共20分)
13题 1
14题 ![]()
1 5题 ![]() 16题 ①③④⑤
16题 ①③④⑤
三、解答题(共6小题,共计70分)
17、连接![]() ,
,
![]() 为异面直线
为异面直线![]() 与
与![]() 所成的角.
连接
所成的角.
连接![]() ,在△
,在△![]() 中,
中,![]() ,
则
,
则![]()
![]() .
.
![]() 异面直线
异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
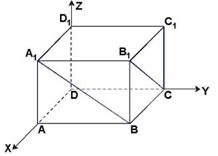
[解法二] 以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 、
、![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴、
轴、![]() 轴,建立空间直角坐标系.
则
轴,建立空间直角坐标系.
则 ![]() , 得
, 得 ![]() .
.
设![]() 与
与![]() 的夹角为
的夹角为![]() ,
,
则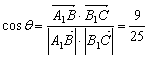 ,
,
![]()
![]() 与
与![]() 的夹角大小为
的夹角大小为![]() ,
,
即异面直线![]() 与
与![]() 所成角的大小为
所成角的大小为![]() .
.
18、方法一:
(I)因为![]() 是
是![]() 的中点,
的中点,![]() ,
,
所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以
![]() ,
,
从而![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
(II)取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,
,
则![]() ,
,
所以![]() 与平面
与平面![]() 所成的角和
所成的角和![]() 与平面
与平面![]() 所成的角相等.
所成的角相等.
因为![]() 平面
平面![]() ,
,
所以![]() 是
是![]() 与平面
与平面![]() 所成的角.
所成的角.
在![]() 中,
中,![]() .
.
故![]() 与平面
与平面![]() 所成的角是
所成的角是![]() .
.
方法二:如图,以![]() 为坐标原点建立空间直角坐标系
为坐标原点建立空间直角坐标系![]() ,设
,设![]() ,则
,则
![]() .
.
(I)
因为![]()
![]() ,
,
所以![]()
(II)
因为![]()
![]() ,
,
所以![]() ,又因为
,又因为![]() ,
,
所以![]() 平面
平面![]()
因此![]() 的余角即是
的余角即是![]() 与平面
与平面![]() 所成的角.
所成的角.
因为![]()
![]() ,
,
所以![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
 19、方法一:
19、方法一:
(I)证明:连结OC
![]()
![]()
在![]() 中,由已知可得
中,由已知可得![]()
 而
而![]()
![]()
![]() 即
即![]()
![]()
![]() 平面
平面![]()
(II) 设点E到平面ACD的距离为![]()
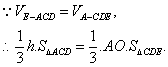
在![]() 中,
中,![]()
![]()
而![]()
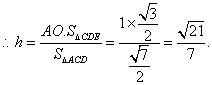
![]() 点E到平面ACD的距离为
点E到平面ACD的距离为![]()
方法二: (I)同方法一。
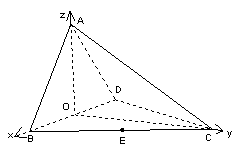 (II)解:以O为原点,如图建立空间直角坐标系,则
(II)解:以O为原点,如图建立空间直角坐标系,则![]()
设平面ACD的法向量为![]() 则
则
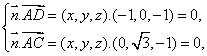
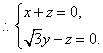
令![]() 得
得![]() 是平面ACD的一个法向量。
是平面ACD的一个法向量。
又![]()
![]() 点E到平面ACD的距离
点E到平面ACD的距离
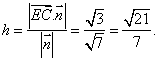
20、解法一:
(Ⅰ)设O为AC中点,连接EO,BO,则EO∥=C1C,又C1C∥=B1B,所以EO∥=DB,EOBD为平行四边形,ED∥OB. ∵AB=BC,∴BO⊥AC,
又平面ABC⊥平面ACC1A1,BOÌ面ABC,故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1,BD⊥AC1,ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线.……6分
(Ⅱ)连接A1E,由AA1=AC=AB可知,A1ACC1为正方形,
∴A1E⊥AC1,又由ED⊥平面ACC1A1和EDÌ平面ADC1知平面
ADC1⊥平面A1ACC1,∴A1E⊥平面ADC1.作EF⊥AD,垂足为F,连接A
不妨设AA1=2,则AC=2,AB=ED=OB=1,EF==,
tan∠A1FE=,∴∠A1FE=60°.
所以二面角A1-AD-C1为60°.
解法二:
(Ⅰ)如图,建立直角坐标系O-xyz,其中原点O为AC的中点.
设A(a,0,0),B(0,b,0),B1(0,b,2c).
则C(-a,0,0),C1(-a,0,2c),E(0,0,c),D(0,b,c).
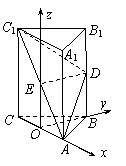 =(0,b,0),=(0,0,2c).
=(0,b,0),=(0,0,2c).
·=0,∴ED⊥BB1.
又=(-2a,0,2c),
·=0,∴ED⊥AC1,
所以ED是异面直线BB1与AC1的公垂线.
Ⅱ)不妨设A(1,0,0),则B(0,1,0),C(-1,0,0),A1(1,0,2),=(-1,-1,0),=(-1,1,0),=(0,0,2),·=0,·=0,即BC⊥AB,BC⊥AA1,又AB∩AA1=A, C⊥平面A1AD.
又 E(0,0,1),D(0,1,1),C(-1,0,1),
=(-1,0,-1),=(-1,0,1),=(0,1,0),·=0,·=0,即EC⊥AE,EC⊥ED,又AE∩ED=E,∴ EC⊥面C1AD.
cos<,>==,即得和的夹角为60°.
所以二面角A1-AD-C1为60°.
21、(1)由题意,![]() ,
,![]() ,
,
![]() 是二面角
是二面角![]() 是直二面角,
是直二面角,
又![]() 二面角
二面角![]() 是直二面角,
是直二面角,
![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() .
.
![]() 平面
平面![]() 平面
平面![]() .
.
(2)由(1)知,![]() 平面
平面![]() ,
,
![]() 是
是![]() 与平面
与平面![]() 所成的角,且
所成的角,且![]() .
.
当![]() 最小时,
最小时,![]() 最大,
最大,
这时,![]() ,垂足为
,垂足为![]() ,
,![]() ,
,![]() ,
,
![]() 与平面
与平面![]() 所成角的最大值为
所成角的最大值为![]() .
.
 22. 解法一:
22. 解法一:
(Ⅰ)证:由已知DF∥AB且![]() DAD为直角,故ABFD是矩形,从而CD
DAD为直角,故ABFD是矩形,从而CD![]() BF.
BF.
又PA![]() 底面ABCD,CD
底面ABCD,CD![]() AD,故由三垂线定理知CD
AD,故由三垂线定理知CD![]() PD.在△PDC中,E、F分别
PD.在△PDC中,E、F分别
PC、CD的中点,故EF∥PD,从而CD![]() EF,由此得CD
EF,由此得CD![]() 面BEF. 第(19)图1
面BEF. 第(19)图1
(Ⅱ)连结AC交BF于G.易知G为AC的中点.连接EG,则在△PAC中易知EC∥PA.又因
PA![]() 底面ABCD,故BC
底面ABCD,故BC![]() 底面ABCD.在底面ABCD中,过C作GH
底面ABCD.在底面ABCD中,过C作GH![]() BD,垂足为H,连接EH.由三垂线定理知EH
BD,垂足为H,连接EH.由三垂线定理知EH![]() BD.从而
BD.从而![]() EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
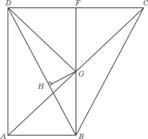 设AB=a,则在△PAC中,有BG=
设AB=a,则在△PAC中,有BG=![]() PA=
PA=![]() ka.
ka.
以下计算GH,考察底面的平面图(如答(19)图2).连结GD.
因S△CBD=![]() BD·GH=
BD·GH=![]() GB·OF.
GB·OF.
故GH=![]() .
.
在△ABD中,因为AB=a,AD=2A,得BD=![]() a 第(19)图2
a 第(19)图2
而GB=![]() FB=
FB=![]() AD-a.DF-AB,从而得
AD-a.DF-AB,从而得
GH=![]() =
= ![]() =
=![]()
因此tanEHG=![]() =
=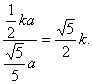
由k>0知![]() 是锐角,故要使
是锐角,故要使![]() >
>![]() ,必须
,必须
![]() >tan
>tan![]() =
=![]()
解之得,k的取值范围为k>![]()
解法二:
(Ⅰ)如图,以A为原点,AB所在直线为x轴,AD所在直线为y轴,AP所在直线为:轴建立空间直角坐标系,设AB=a,则易知点A,B,C,D,F的坐标分别为
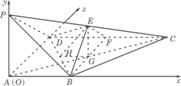 A(0,0,0),B(a,0,0),C(
A(0,0,0),B(a,0,0),C(
F(a,
从而![]() =(2a,0,0),
=(2a,0,0), ![]() =(0,2a,0),
=(0,2a,0),
![]() ·
·![]() =0,故
=0,故![]()
![]()
![]() .
.
设PA=b,则P(0,0,b),而E为PC中点.故 第(19)3
E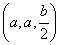 .从而
.从而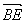 =
=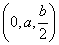 .
.
![]() ·
·![]() =0,故
=0,故![]()
![]()
![]() .
.
由此得CD![]() 面BEF.
面BEF.
(Ⅱ)设E在xOy平面上的投影为G,过G作GH![]() BD垂足为H,由三垂线定理知EH
BD垂足为H,由三垂线定理知EH![]() BD.
BD.
从而![]() EHG为二面角E-BD-C的平面角.
EHG为二面角E-BD-C的平面角.
由PA=k·AB得P(0,0,ka),E![]() ,G(a,a,0).
,G(a,a,0).
设H(x,y,0),则![]() =(x-a,y-a,0),
=(x-a,y-a,0), ![]() =(-a,2a,0),
=(-a,2a,0),
由![]() ·
·![]() =0得=a(x-a)+2a(y-a)=0,即
=0得=a(x-a)+2a(y-a)=0,即
x-2y=-a ①
又因![]() =(x,a,y,0),且
=(x,a,y,0),且![]() 与
与![]() 的方向相同,故
的方向相同,故![]() =
=![]() ,即
,即
2x+y=
由①②解得x=![]() a,y=
a,y=![]() a,从而
a,从而![]() =
=![]() ,|
,|![]() |=
|=![]() a.tanEHG=
a.tanEHG=![]() =
=![]() =
=![]() .
.
由k>0知,EHC是锐角,由![]() EHC>
EHC>![]() 得tanEHG>tan
得tanEHG>tan![]() 即
即
![]() >
>![]() 故k的取值范围为k>
故k的取值范围为k>![]() .
.