高二理科数学下学期第一次月考试题
(考试时间:120分钟 总分:150分)
命题人:漳平一中 苏德林 审题人:漳平一中 陈炳泉
一、选择题(每小题5分,共60分)
1、若复数![]() 则
则![]() 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2、一个口袋内装有大小相同的6个白球和2个黑球,从中取3个球,则共有( )种不同的取法
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、在用数学归纳法证明等式![]() 时,当
时,当![]() 时的左边等于( )
时的左边等于( )
A、1 B、2 C、3 D、4
4、曲线![]() 在
在![]() 处的切线的倾斜角是( )
处的切线的倾斜角是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
5、定义运算![]() ,则符合条件
,则符合条件![]()
![]() 的复数
的复数![]() 的值为( )
的值为( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、函数![]() ,
,![]() 的最大值、最小值分别是( )
的最大值、最小值分别是( )
A、3,-17 B、1,-1
C、1,-17 D、9,-19
7、平面内平行于同一直线的两直线平行,由类比思维,我们可以得到( )
A、空间中平行于同一直线的两直线平行
B、空间中平行于同一平面的两直线平行
C、空间中平行于同一直线的两平面平行
D、空间中平行于同一平面的两平面平行
8、旅游公司为3个旅游团提供4条旅游线路,每个旅游团只能任选其中一条,则不同的选择方法有( )
A、24 B、48 C、64 D、81
9、![]() 等于( )
等于( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
10、![]() 则
则![]() 等于( )
等于( )
A、0 B、![]()
C、![]() D、
D、![]()
11、5个男生,2个女生排成一排,若女生不能排在两端,但又必须相邻,则不同的排法有( )
A、480 B、
12、设![]() 分别是定义在R上的奇函数和偶函数,且
分别是定义在R上的奇函数和偶函数,且![]() ,当
,当![]() 时,
时,![]() 且
且![]() 则不等式
则不等式![]() 的解集是( )
的解集是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
二、填空题(每小题4分,共16分)
13、若![]() 则
则![]() =
=
14、![]()
15、垂直于直线![]() 且与曲线
且与曲线![]() 相切的直线方程的一般式是
相切的直线方程的一般式是
16、设![]()
![]() ,
,![]() 则圆
则圆![]() 可以表示 个大小不等的圆, 个不同的圆,(位置不同或大小不等)(用数学作答)
可以表示 个大小不等的圆, 个不同的圆,(位置不同或大小不等)(用数学作答)
“华安、连城、永安、漳平一中,龙海二中” 五校联考
 2007-2008学年下学期第一次月考
2007-2008学年下学期第一次月考
高二理科数学试题
| 选择题 | 填空题 | 17 | 18 | 19 | 20 | 21 | 22 | 总分 |
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题:
13、 14、 15、 16、
三、解答题
17、计算求值(本题满分12分,每小题6分)
(1)计算![]() (2)已知复数
(2)已知复数![]() 满足
满足![]() 求
求![]()
18、(本题满分12分)
已知曲线![]()
(1)求曲线在点![]() 处的切线方程(2)求曲线过点
处的切线方程(2)求曲线过点![]() 的切线方程
的切线方程
19、(本题满分12分)从8名运动员中选4人参加4×100米接力赛,在下列条件下,各有多少种不同的排法?(用数字结尾)
(1)甲、乙两人必须跑中间两棒
(2)若甲、乙两人只有一人被选且不能跑中间两棒
(3)若甲、乙两人都被选且必须相邻两棒
20、(本题满分12分)已知数列![]() 前
前![]() 项和为
项和为![]() 且
且![]() ,
,![]()
(1)试求出![]() ,
,![]() ,
,![]() ,
,![]() ,并猜想
,并猜想![]() 的表达式
的表达式
(2)证明你的猜想,并求![]() 的表达式
的表达式
21、(本题满分12分)设函数![]()
![]() 图象关于原点对称,且
图象关于原点对称,且![]() 时,
时,![]() 取极小值
取极小值![]()
(1)求![]() 的值
的值
(2)当![]() 时,图象上是否存在两点,使得过两点处切线互相垂直?试证明你的结论。
时,图象上是否存在两点,使得过两点处切线互相垂直?试证明你的结论。
22、(本题满分14分)已知函数![]() 在
在![]() 处取得极值
处取得极值
(1)求实数![]() 的值;
的值;
(2)若![]() 时
时![]()
![]() 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(3)证明对任意的正整数![]() ;不等式
;不等式![]() 都成立
都成立
“华安、连城、永安、漳平一中,龙海二中” 五校联考
2007-2008学年下学期第一次月考
高二理科数学参考答案
一、选择题(每小题5分,共60分)、
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | C | C | B | A | D | C | B | A | B | A |
二、填空题(每小题4分,共16分)
13、190 14、![]() 15、
15、![]() 16、3,36
16、3,36
17、解(1)![]()
![]()
![]()
![]()
![]()
(2)设![]()
则![]()
![]()
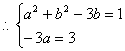
![]() 或
或![]()
![]() 或
或![]()
18、解:(1)![]()
![]()
![]() 所求切线方程为
所求切线方程为![]() 即
即![]()
(2)设切点![]()
则切线方程为![]() 又切线过点
又切线过点![]()
![]()
![]() 或
或![]()
![]() 切线方程为
切线方程为![]() 或
或![]()
19、解:(1)![]()
(2)![]()
(3)![]()
20、解:(1)![]()
![]()
![]()
![]()
猜想![]()
(2)证明①当![]() 时
时 ![]() 成立
成立
②假设![]()
![]() 时,
时,![]() 成立
成立
那么![]() 时
时
![]()
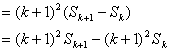
![]()
![]() 时命题成立
时命题成立
由①②可知,对于一切![]()
![]() 均成立
均成立
由![]()
21、解:(1)![]() 图象关于原点对称
图象关于原点对称
![]()
![]()
![]()
![]() 恒成立
恒成立
![]()
![]()
![]()
![]()
![]()
![]()
![]() 且
且![]()
![]()
![]()
![]()
![]()
(2)当![]() 时,图象上不存在这样的两点,使结论成立。
时,图象上不存在这样的两点,使结论成立。
(反证法):假设图象上存在两点![]() 使得过此两点处切线互相垂直,则由
使得过此两点处切线互相垂直,则由![]() 知两点处的切线斜率分别为
知两点处的切线斜率分别为![]()
![]() 且
且![]() ①
①
![]()
![]()
![]() 这与①式矛盾
这与①式矛盾
故假设不成立
22、解:(Ⅰ)![]()
![]() 时,
时,![]() 取得极值,
取得极值,![]() ,
,
故![]() 解得
解得![]() 经检验
经检验![]() 符合题意。
符合题意。
(Ⅱ)由![]() 知
知![]() 由
由![]()
得![]() ,
,
令![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,于是
,于是![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,于是
,于是![]() 在
在![]() 上单调递减。
上单调递减。
![]()
![]()
