高二理科数学下学期考试卷

时量：120分钟　　　 满分：150分

命题人：胡雪文　 　校审人：江楚珉

一、选择题（本大题共10小题，每小题5分，共50分.选对的得5分，错选或不答得0分.）

1．若直线a，b，c满足a∥b，b与c不平行，则（　　）

A．a与c平行　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．a与c不平行

C．a与c是否平行不能确定　　　　　　　　　　　　　　　　 D．a与c是异面直线

2．从1、2、3、4、5这五个数字中任取3个组成无重复数字的三位数，当三个数字有

2和3时(可以没有)，则2需排在3的前面(不一定相邻)，这样的三位数有　　　 （　　 ）

　 A．9个　　　　　B．15个　　　　C．45个　　　　 D．51个

3．下列命题正确的是（　　）

A．一条直线与一个平面平行，它就和这个平面内的任意一条直线平行

B．平行于同一个平面的两条直线平行

C．与两个相交平面的交线平行的直线，必平行于这两个平面

D．平面外的两条平行直线中的一条与一个平面平行，则另一条直线也与此平面平行

4．随机事件A的概率P(A)满足　　　　　　　　　 (　　 )

A.P(A)=0　 　 　B.P(A)=1　　　　　 C.P(A)>1　　　　 D.

5．空间四边形OABC中，= a，= b，= c，点M是在OA上且OM = 2MA，N为BC的中点，则等于（　　）

A．ab +c　　　　　B．a +b +c　　　C．a +bc　　　　 D．a +bc

6．若直线l与平面所成角为，直线a在平面内，且与直线l异面，则直线l与直线a所成的角的取值范围是（　　）

A．　　　　　　　　　　B．　　　　　　　　 C．　　　　　　　　 D．

7．长方体的一个顶点处的三条棱长之比为1:2:3，它的表面积为88，则它的对角线长为（　　）

A．12　　　　　　　　　　　　　 B．24　　　　　　　　　　　　　C．　　　　　　　　　　 D．

8．二项式的展开式中的系数是 （  ）

A、6　　　 B、12　　　 C、24　　　　 D、48

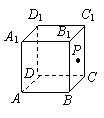9．如图，在正方体ABCD—A₁B₁C₁D₁中，P是侧面BB₁C₁C内一动点，若P到直线BC与直线C₁D₁的距离相等，则动点P的轨迹所在曲线是（　　）

A．直线　　　　　　　　B．圆　　　　　 C．双曲线　　　　　 D．抛物线

10．过双曲线的右焦点F，作渐近线的垂线与双曲线左、右两支都相交，则双曲线的离心率e的取值范围是（　　）

A．1＜e＜2　　　　　　　　B．1＜e＜　　　　　　 C．e＞　　　　　　　　　D．e＞2

二、填空题（每小题5分，共20分）

11．从分别写有A,B,C,D,E的5张卡片中,任取2张,这2张上的字母恰好按字母顺序相邻的概率为________________.

12．过抛物线y² = 8x的焦点，倾斜角为45°的直线的方程是　　　　　　　　　　　　　　.

13．方程表示焦点在y轴上的椭圆，则m的取值范围是　　　　　　　　　　　　 .

14．正四面体A—BCD的棱长为1，则A到底面BCD的距离为　　　　　　 .

15．已知正三棱柱ABC—A₁B₁C₁的各棱长相等，M是BB₁的中点，则面AC₁M与面ABC成的锐二面角是　　　　　　　 　　　 .

　

座位号

数学考试答卷

08年元月26日

年级

高二

科目

理科数学

时 量

120分钟

	一、选择题（每小题5分，共50分） 题号 1 2 3 4 5 6 7 8 9 10 答案 二、填空题（每小题5分，共25分） 11．　　　 　 　　 　　　　12．　　　　　　　  　　　 13．　　　　　　 14．　　　　　　　 　　　15．　　　　　　　  三、解答题（75分） 16．（12分）如图，在直三棱柱ABC—A1B1C1中，∠ACB = 90°，点D是AB的中点. （1）求证：AC⊥BC­1； （2）求证：AC1∥平面CDB­1. 17．（12分）△ABC的两个顶点A、B的坐标分别是(–6, 0)，(6, 0)，边AC、BC所在直线的斜率之积等于常数（≠0，∈R），讨论顶点C的轨迹是什么？

年　 级

班　 次

姓　 名

考　 号

考室号

 

考　室 座位号 成　绩

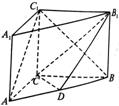
18．（12分）已知三棱锥A—BCD的侧棱AB⊥底面BCD，BC = CD，∠BCD = 90°，∠ADB = 30°，E、F分别是侧棱AC、AD的中点.

（1）求证：平面BEF⊥平面ABC；

（2）求平面BEF和平面BCD所成的角.

19．（12分）抛物线上有两点A (x₁, y₁)，B (x₂, y₂)，且= 0，又知点M (0, –2). （1）求证：A、M、B三点共线； （2）若，求AB所在的直线方程.

20．（13分）如图，在棱长为4的正方体ABCD—A₁B₁C₁D₁中，O是正方形A₁B₁C₁D₁的中心，点P在棱CC₁上，且CC₁ = 4CP.（1）求直线AP与平面BCC₁B₁所成角的大小；（结果用反三角函数值表示）;（2）设O点在平面D₁AP上的射影是H，求证：D₁H⊥AP；（3）求点P到平面ABD₁的距离.

21.(14分)从原点出发的某质点M，按向量移动的概率为，按向量移动的概率为，设M可到达点（0，n）的概率为.　(1)求P₁和P₂的值； （2）求证：=;　(3)求的表达式。

　

湖南省邵东一中高二数学期末考试参考答案（理）

一、选择题（每小题5分，共50分）

1．B　　　2．D　　　3．D　　　4．D　　　5．B　　　6．D　　　7．C　　　8．C　　　9．D　　　10．C

二、填空题（每小题5分，共25分）

11．　 12．x – y – 2 = 0　　　　13．8＜m＜25　　 14．　　 15．45°　　　　　

三、解答题

16．（12分）（1）证：∵棱柱ABC—A₁B₁C₁为直棱柱，∴C₁C⊥面ABC，∴C₁C⊥AC，

又∵AC⊥BC，∴AC⊥平面BB₁C₁C，∴AC⊥BC₁.

（2）设BC₁∩B₁C = E，连结DE，∵D、E分别为AB、BC₁的中点，∴DE∥AC₁.

又∵AC₁平面CDB₁，平面CDB₁，∴AC₁∥平面CDB₁.

17．（12分）解：设顶点的坐标为C(x, y)，则(x≠±6).

而k_AC·k_BC =，即，化简得(x≠±6).

（1）当＜–1时，顶点C的轨迹是焦点在y轴上的椭圆，并去掉A、B两点.

（2）当= –1时，顶点C的轨迹是以原点为圆心的圆，并去掉A、B两点.

（3）当–1＜＜0时，顶点C的轨迹是焦点在x轴上的椭圆，并去掉A、B两点.

（4）当＞0时，顶点C的轨迹是焦点在x轴上的双曲线. 并去掉A、B两点.

18．（12分）解：（1）∵AB⊥底面BCD，∴AB⊥CD，又∵BC⊥CD，∴CD⊥平面ABC.

∵E、F分别为AC、AD的中点，∴EF∥CD.

∴EF⊥平面ABC，∴平面BEF⊥平面ABC.

（2）设平面BEF与面BCD交线为l，则B∈l (如图).

∵EF∥DC，面BEF，∴DC∥面BEF.

∵面BCD∩面BEF = l，面BCD，∴DC∥l.

又DC⊥平面ABC，∴l⊥面ABC. 面ABC与面BEF、面BCD交于BE、BC，

∴∠EBC是二面角BEF—l—BDC所成的平面角.

过E作EG⊥BC于G，又AB⊥BC，　　

∴EG∥AB，且EG =AB.

设BC = CD = 1，则BG =，BD =，

又∠ADB = 30°，∴.

∴tan∠EBG =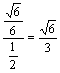. ∴平面BEF和平面BCD所成的角为arctan.

19．（12分）解：设，∵，∴= 0 (x₁x₂≠0).

∴x₁x₂ = – 4.

又∵，.

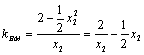代代入k_AM得，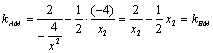

∴A、M、B三点共线.

（2）∵，∴

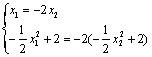
∴，∴. 即或.

∴或，∴AB的方程为.

20．（13分）（理）解：如右图，（1）解：∵AB⊥平面BCC₁B₁，

∴AP与平面BCC₁B₁所成的角主浊∠APB.

如右图建立空间直角坐标系，坐标原点为D.

∵CC₁ = 4CP，CC₁ = 4，

∴CP = 1，A (4, 0, 0)，P (0, 4, 1)，B (4, 4, 0).

∴.

∵,

∴cos∠.

∴直线AP与平面BCC₁B₁所成的角为arccos.

（2）证明：连结D₁O，由（1）有D₁ (0, 0, 4)，O (2, 2, 4)，

∴.　　 ∴.

∵平面D₁AP的斜线D₁O在这个平面内的射影是D₁H，∴D₁H⊥AP.

（3）解：连结BC₁，在平面BCC₁B₁中，过点P作PQ⊥BC₁于点Q.

∵AB⊥平面BCC₁B₁，平面BCC₁B₁，∴PQ⊥AB.

∴PQ⊥平面ABC₁D₁. ∴PQ就是点P到平面ABD₁的距离.

在Rt△C₁PQ中，∠C₁QP = 90°，∠PC₁Q = 45°，PC₁ = 3，

∴，即点P到平面ABD_­1的距离为.

21(14分)解：（1）P₁= ，P₂=（）²+=

（2）证明：M到达点（0，n+2）有两种情况：①从点（0，n+1）按向量移动；②从点（0，n）按向量移动.令质点到达(0,n)的事件分别为,质点M按平移的事件记为A,质点M按平移的事件记为B.则这些事件互斥且互相独立,从而有:

 　　 ∴=

（3）数列{}是以P₂-P₁为首项，-为公比的等比数列.

,

又∵=（）+（）+…+(P₂-P₁)