高二理科数学下期阶段考考试卷

数学试卷(Ⅰ)  

（完卷时间：120分钟　　　满分：150分）

一、填空题：（本大题18小题，每小题5分，共90分，在答题卡上的相应题目的答题区域内作答。）

1.　　从A地到B地有3种走法，从B地到C地有2种走法，从A地不经过B地到C地有5种走法，则从A地到C地的不同走法有　 　　　　种

2.　　化简：　　　　　　

3.　  4名同学参加运动会中的跳高、铅球、长跑三个项目，每人限报一项的种数有　

4.　　展开式中的常数项是　　　　 

5.　　4张卡片，分别写有4，5，6，7这4个数，现从中任取3个数组成三位数，若写有6的卡片可当作9使用，则这样的三位数共有　　　　　个　

6.　　用数学归纳法证明第二步证明从“k到k+1”，左端增加的项数是　 　　 

7.　　有5个座位连成一排，现安排2个人就座，则恰好有两个空位相连的不同座法有

　　　种

8.　　从这6个数中任取3个数字分别作为直线中的，所得的经过坐标原点的直线有　　 　条．

9.　　如图，在某城市中，M、N两地间有整齐的道路网，若规定只能

向东或向北两个方向沿图中的矩形的边前进，则从M到N不同的

走法共有　　　　　 

10.　　　　　　 安排3名支教老师去6所学校任教，每校至多2人，则不同的分配方案共

有　 　　 种.

11.　　　　　　 如图第n个图形是由正+2边形“扩展”而来,（ｎ＝１，２，３，…）。

则第10个图形中共有________个顶点。

12.　　　　　　 设（为虚数单位）则A=的值是　　　

13.　　　　　　 设，则的值为　　　　　 

14.　　　　　　 从不同号码的4双鞋中任取只，其中恰好有双的取法种数为　　　

15.　　　　　　 幻方就是把１，２，３，……，n²排成一个n行n列的方阵，使得每行中的各数之和、每列中的各数之和以及两条对角线中的各数之和都是同一个数，称作“n阶幻方”，数称为“幻和”。则=　　　　　　　  　.

16.　　　　　　 将数字1，2，3，4，5，6拼成一列，记第个数为，若，，，，则不同的排列方法有　　　 种（用数字作答）．

17.　　　　　　 三行三列的方阵中有9个不同的数，从中任取三个数，则至少有两个数位于同行或同列有　　  种不同的方法。

18.　　　　　　 下列四个类比推理得到的结果不正确的是　　　　　 （写出所有不正确的序号）

①　　平面内正三角形的“三边相等，三内角相等”的性质可类比正四体各个面都是全等的正三角形，相邻两个面所成的二面角相等；

②　   =类比

③　若是等差数列的前项和，公差为，则数列

也成等差数列，且公差为，类比若是等比数列

的前项积，公比为，则有.

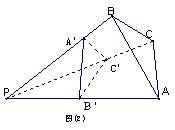
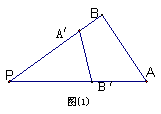
④ 由图(1)有面积关系:

则由(2) 有体积关系:

二、解答题：（本大题共4小题，共60分，解答写出文字说明、证明过程或演算步骤）

19.　　　　　　 袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为现有甲、乙两人从袋中轮流摸取1球，甲先取，乙后取，然后甲再取……取后不放回，直到两人中有一人取到白球时既终止，每个球在每一次被取出的机会是等可能的，用表示取球终止所需要的取球次数.

（1）求袋中所有的白球的个数；

（2）求随机变量的概率分布；

20.　　　　　　 （1）用分析法证明：

（2）用反证法证明：如果，那么。

21.　　　　　　  已知的展开式中前三项系数成等差数列。

（1）展开式里所有的x的有理项； 

（2）求展开式里系数最大的项。

22.　　　　　　 　　 已知数列满足,　

( 1 )　写出,并推测的表达式；

( 2 )　用数学归纳法证明所得的结论。

（3 ） 把数列的所有数按照从小到大的

序号、左小右大的原则写成如右数表：

第k行有个数,第t行的第s个数

（从左数起）记为A（t,s）,求通项公式A(t,s)（用t,s来表示）