高二（必修3）模块测试卷数学试题（理科）

（时间：120分钟　 满分：150分）

说明：请将答案填写在答卷纸上，考试结束后只交答案卷。

一、选择题（本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的）.

1．已知定点F₁、F₂，且F₁F₂=6，动点P满足PF₁-PF₂=6，则动点P的轨迹是　　　（　　）

　　　 A． 椭圆　 　　　　　　B． 双曲线　　　　　 C． 线段　　 　　　　D． 射线

2．若直线的方向向量为=(1,0,2),平面的法向量为=(-2,0,-4),则　　　　　　　　　　 （　　）

　　　 A． 　　　　 B． ∥　　  　　C． 　　　　　　D． 与斜交

3．复数z=()是纯虚数，则的值为　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 1　　　　 　　　 B． 　　　　　　　C． 1或　　　　　 D．

4．过点M（2，4）作直线与抛物线y²=8x只有一个公共点，则这样的直线条数是　（　　）

　　　 A． 0　　　　　 　 B． 1 　　　　　　　　 C． 2　　　　 　　　 D． 3

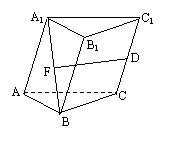5．在三棱柱ABC－A₁B₁C₁中，D是CC₁的中点，F是A₁B的中点，且，则（　　）

　　　 A．　　　　　　　　　　　　　　　　

　　　 B．　

　　　 C．　　　　　　　　　　　　　　　　

　　　 D．

6．若抛物线y=x²的准线方程是y=1，则的值为　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A． 　　　　　　 B． 　　　　　 C． 4　　　　　  D． -4

7．已知椭圆的左、右焦点分别是F₁，F₂，P是椭圆上一点，若PF₁=3PF₂，则点P到左准线的距离是　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A． 2　　 　　　　　　　B． 4 　　　　　　　　　C． 6　　　　 　　　 D． 8

8．在长方体ABCD－A₁B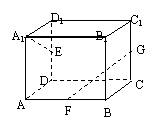₁C₁D₁中，AA₁＝AB＝2,AD＝1,点E,F,G分别是DD₁，AB，CC₁的中点，则异面直线A₁E与GF所成角的余弦值为　　　　　　　　　　　　　　　　　　　　　（　　）

　　 A． 　　　　　B． 　　　　

　　　C． 　　　　　 D． 0

9．已知抛物线的方程为，过焦点的弦PQ的长为8，PQ的中点M到抛物线的准线的距离为　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A． 4　　　 　　　　　B． 5 　　　　　　　 C． 6　　　　　　　　　 ． 8

2,4,6

10．已知方程 和 （其中），它们所表示的曲线可能是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）.

Ａ　　　　　　　　 Ｂ　　　　　　　　Ｃ　　　　　　　Ｄ

11．椭圆的四个顶点分别为A、B、C、D，若菱形ABCD的内切圆恰好过椭圆的焦点，则椭圆的离心率的平方是　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A． 　　　　　B． 　　　　　C． 　　　　　 D．

12．对于直角坐标系内任意两点P₁(x₁,y₁)、P₂(x₂,y₂),定义运算“”为：P₁P₂=(x₁,y₁) (x₂,y₂)=若点M是与坐标原点O相异的点，且M（1，1）=N，则∠MON的大小为　　　　　　　　（　　）.

　　　 A． 90º　 　　　　　　　B． 60º　　 　　　　　C．45º 　　　　　　　D． 30º

二、填空题（本大题共4个小题，每小题4分，共16分，把答案写在横线上．）

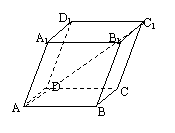13．已知平行六面体ABCD-A₁B₁C₁D₁中，AB=AD=AA₁=1，

∠BAD=∠BAA₁=∠DAA₁=60º，则=　　　　.

14．若双曲线的焦点到它相应准线的距离是1，

则k＝　.

15．菱形ABCD的边长为a，∠A=60⁰，将该菱形沿对角线

BD折成直二面角，则AC与BD的距离为　　　　　  .

16．有一隧道，内设双行线公路，同方向有两个车道

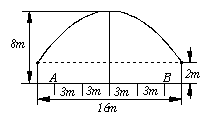
（共有四个车道），每个车道宽为3m，此隧道的

截面由一个长方形和一抛物线构成，如图所示，

隧道高8m,宽16m. 为保证安全，要求行驶车辆

顶部（设为平顶）与隧道顶部在竖直方向上高度

之差至少为，靠近中轴线的车道为快车道，

两侧的车道为慢车道，则车辆通过隧道时，慢车

道的限制高度为　　　　　　 （用分数表示）.

三、解答题(本大题共6小题，满分74分，解答应写出文字说明，证明过程或演算步骤)．

17．（本题满分10分）若双曲线与椭圆有相同的焦点，与双曲线有相同渐近线，求双曲线方程.

18．（本题满分12分）已知复数，

　 （1）求的值；

　 （2）若，求实数、的值.

19．（本题满分14分）如图所示，多面体ABCDS中，面为矩形，SD⊥AD，SD⊥AB，且，，

M、N分别为AB、CD中点.

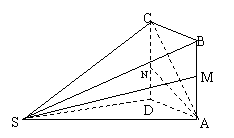　 （Ⅰ）求证：SM⊥AN；

　 （Ⅱ）求二面角A—SC—D的余弦值；

　 （Ⅲ）若AB=，求点D到平面ASC的距离.

20．（本题满分12分）设抛物线的准线与轴的交点为C，过点C作直线交抛物线于A、B两点，求线段AB中点M的轨迹方程.

21．（本题满分13分）如图，在各棱长均为2的三棱柱ABC-A₁B₁C₁中，点A₁在底面ABC内的射影O恰为线段AC的中点.

　 （Ⅰ）求侧棱AA₁与平面A₁BC所成角的正弦值；

　 （Ⅱ）已知点D为点B关于点O的对称点，在直线AA₁上是否存在点P，使DP∥平面AB₁C？若存在，请确定点P的位置；若不存在，请说明理由.

22．（本题满分13分）已知椭圆的离心率.

　 （Ⅰ）若椭圆准线间的距离为，求椭圆方程；

　 （Ⅱ）直线过点C(交椭圆于A、B两点，且满足：，试求面积的最大值.

附加题：（本题解答正确完整给10分，不答或答错不扣分）

有对称中心的曲线叫做有心曲线,显然圆、椭圆、双曲线都是有心曲线. 过有心曲线的中心的弦叫有心曲线的直径,（为研究方便,不妨设直径所在直线的斜率存在）.

　　　 　　定理：过圆上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值－1．

　　（Ⅰ）写出该定理在椭圆中的推广,并加以证明；

　 　（Ⅱ）写出该定理在双曲线中的推广；你能从上述结论得到有心圆锥曲线（包括椭圆、双曲线、圆）的一般性结论吗？请写出你的结论.

参考答案

一、1．D　2．A　3．B　 4．C　 5．A　6．B　7．C　 8．D　 9．A　 10．B　11．B　12．C

2,4,6

二、13．　　14．2　　15．　 16．

三、17．解：设所求的双曲线方程为，依题意可知，

化为标准方程为，　　　　　　　　　　

由于椭圆的焦点为(0,)，所以，，　　　 　　　　　　　　　

双曲线方程为　　　　　　　　　　　

18．解：z=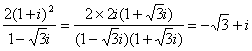

（Ⅰ）=

　　　　　　　　  =-2

　　　　　　　　  =

（Ⅱ）∵

∴()²+2()+=1+bi

∴(a-4)+i=1+bi

∴　a-4=1

　　b=1　　　　

∴a=5,　b=1

19．解：（I）建立如图所示的空间直角坐标系，设AD=1，

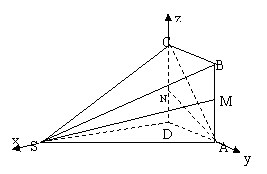则A(0,1,0),N(0,0,1),S(,0,0),M(0,1,1),

C(0,0,2)

,

 

∴SM⊥SM

　 （Ⅱ）设平面SAS的法向量为，，=(0,-1,2)

则　　　　　

　　　　　　∴　 y=6

　　　　　　　　　　　　　　　　 Z=3

　又平面SDC的一个法向量

设二面角A－SC－D的平面角为θ，

则　

∴二面角A－SC－D的余弦值为

　 （Ⅲ）∵　平面ASC法向量为

∴D到平面ASC的距离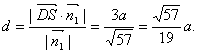

20．解：∵抛物线准线与x轴交点C(0,1)

　　　 ∴设直线的方程为y=kx+1　 且A(x₁,y₁)，B(x₂,y₂)

由  y=kx+1，得: x²+4kx+4=0

　　x²=-4y

∴x₁+x₂=-4k　　

∴y₁+y₂=k(x₁+x₂)+2=-4k²+2　　　

M(x,y)是AB的中点,

 x=　

y=　　 

消去k得：

∵交抛物线于两点，∴Δ=16k²-16>0　 ∴k>1或k<-1　 ∴x>2或x<-2

故点M的轨迹方程为：( x>2或x<-2).

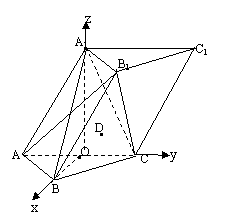21．解：以O为坐标原点，DB，OC，OA₁依次为轴、轴，轴正方向建立空间直角坐标系，则点A₁(0,0,)，A(0,-1,0)，B(,0,0)，C(0,1,0)

　 （Ⅰ），

设平面A₁BC的一个法向量为

则　

∴=(

设直线AA₁与平面A₁BC所成角为θ

则　sinθ=cos<,>=

即侧棱AA₁与平面A₁BC所成角正弦值为.

　 （Ⅱ）设B₁(，则

∵　

∴=　∴

∴B₁,　 

∴

设平面ACB₁的一个法向量是，

则　

　　　　  　　　　　　　　　∴=(-1,0,1)

假设在AA₁上存在P(0,m,n)使DP∥平面AB₁C,

∵D、B关于O对称　　∴D　　∴=(,m,n)

∴=　 ∴n=

故当点P与A₁重合时，DP∥平面AB₁C．

22．解：（Ⅰ）∵椭圆的方程为(a>b>0)

由e=,及a²=b²+c²,得a²=3b²

又由准线间的距离为，得2

∴a²=3,b²=1　　　　 ∴椭圆方程为.

　 （Ⅱ）由e=,及a²=b²+c²,得a²=3b², 可设椭圆的方程为

设A(x₁,y₁) , B(x₂,y₂)　由题知直线的斜率存在，则设的方程为y=k(x+1),

由　　y=k(x+1)　　　

　　　　　 得：(3k²+1)x²+6k²x+3k²-3b²=0

且Δ=12(3b²-1)k²+12b²

∵直线交椭圆于两点，且　∴点C在椭圆内部，∴a>1

∴3b²>1　  ∴Δ>0

∴x₁+x₂=　

∵　∴(x₁+1,y₁)=3(-1-x₂,-y₂)　 ∴x₁=-4-3x₂

∴x₂+1=　 ∴x₁-x₂=

又O到直线的距离为d=

∴

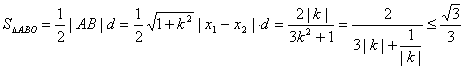
∴当且仅当3k=,即时，取最大值.

附加题：解：（Ⅰ）设直径的两个端点分别为A、B,由椭圆的对称性可得,A、B关于中心O（0,0）对称,所以A、B点的坐标分别为A（,B（.

P（上椭圆上任意一点,显然,

因为A、B、P三点都在椭圆上,所以有

, ①

,　②.

而,

由①－②得：.

所以该定理在椭圆中的推广为：过椭圆上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值.

　 （Ⅱ）在双曲线中的推广为：过双曲线上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值

　　　 　　该定理在有心圆锥曲线中的推广应为：过有心圆锥曲线上异于 直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值－

高二上数学寒假作业

1．重新整理完成期末复习提纲；

2．认真订正期考试卷；

3．完成《优化单元测试卷》中4-1到4-4的“综合测评”部分；

4．完成《三维设计》中p92—p94/复数章末过关检测；

5．预习选修2-2中第一章的内容。

（以上1-4点的作业在下学期开学第一天交）