高二第一学期期中考试数学试卷
（考试时间90分钟，满分100分）
命题：吴世星 审核：李家齐
一、填空题（共12小题，每题3分，共36分）
1、
设
，点
的坐标为
，则点
的坐标为__________.
2、
设
，
是与
同向的单位向量，则的坐标是__________.
3、
若等差数列
的公差
，
，则它首项
=__________.
4、
若等比数列中，
，则它的公比
=__________.
5、
计算：
=__________.
6、
已知向量
，若
三点共线，则
=__________.
7、
，则
与
的夹角是__________.
8、
已知
为平行四边形
内一点，设
，则
=__________.
9、
在
与
之间插入两个数，得到数列
，其中前三个数成等差数列，后三个数成等比数列，则其中的一组数列是 __________.
10、已知无穷等比数列各项的和是
，则首项的取值范围是__________.
11、对
个向量
，如果存在不全为零的实数
使得
，则称线性相关.若已知
，
，
是线性相关的，则
=__________________.
12、若数列是等差数列，则数列
也为等差数列；类比上述性质，相应地，若数列
是等比数列，且
，则有
=____________也是等比数列.
二、选择题（共4小题，每题3分，共12分）
13、下列各式中错误的是…………………………………………………………………（ ）
A.
B.
C.
D.
14、已知
，
为线段
的中点，则向量
与
的夹角是（ ）
A.
B.
C. 
D.
15、已知等差数列中，
，则
的值是………………………（ ）
A. 
B. 
C. 
D. 
16、在△
中，有命题①若
，则△为锐角三角形②
③
,则△为等腰三角形 ④
.上述命题正确的是…………………………………………………………………………………………（ ）
A.①② B. ①④ C. ②③ D. ②③④
二、解答题（共6小题，第17题6分，第18、19、20题每题8分，第21题10分，第22题12分，共52分）
17 已知
，且
∥
，
，求点
的坐标.
18 已知一个等差数列的前项的和是
，前
项的和是.求此等差数列的前项和
，并求出当为何值时，最大，最大值是多少？
19设数列的首项
，且
（
）.（1）求
；
（2）根据上述结果猜想数列的通项公式，并用数学归纳法加以证明.
20、在一次人才招聘会上，有甲、乙两家公司分别公布它们的工资标准：
甲公司：第一年月工资数为1500元，以后每年月工资比上一年月工资增加230元；
乙公司：第一年月工资数为2000元，以后每年月工资在上一年的月工资基础上递增5%.
设某人年初同时被甲、乙公司录取，试问：
（1）
若该人打算连续工作年，则在第年的月工资收入分别是多少元？
（2） 若该人打算连续工作10年，且只考虑工资收入的总量，该人应该选择哪家公司？为什么？(精确到1元)
21、已知
，
分别是与
轴，
轴正方向相同的单位向量，
，对任意正整数，
.
（1）若
，求
的值；
（2）求向量
.
22、我们在下面的表格中填写数值：先将第1行的所有空格填上1；再把一个首项为1，公比为的数列依次填入第一列的空格内；然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其他空格.
| 第1列 | 第2列 | 第3列 | …… | 第 | |
| 第1行 | 1 | 1 | 1 | …… | 1 |
| 第2行 |
| ||||
| 第3行 |
| ||||
| …… | …… | ||||
| 第 |
|
（1）按照填写规则，请在上述表格内填写第二行的空格以及第二列的空格；
（2）试用、表示第二列的各数之和；
（3）设第3列的数依次为
，若
成等比数列，试求的值；能否找到的值，使得数列的前
项
成为等比数列？若能找到，的值有多少个？若不能找到，说明理由.
上海南汇中学2007学年第一学期高二期中考试
数学答案及评分标准
（考试时间90分钟，满分100分）
命题：吴世星 审核：李家齐
三、填空题（共12小题，每题3分，共36分）
10、
设，点的坐标为，则点的坐标为___
___.
11、
设，是与同向的单位向量，则的坐标是_
___.
12、
若等差数列的公差，，则它首项=___
_______.
13、
若等比数列中，，则它的公比=__________.
14、
计算：=____
______.
15、
已知向量，若三点共线，则=________.
16、
，则与的夹角是____
______.
17、
已知为平行四边形内一点，设，则=_
__.
18、
在与之间插入两个数，得到数列，其中前三个数成等差数列，后三个数成等比数列，则其中的一组数列是 ___
或（
）_____.
19、
已知无穷等比数列各项的和是，则首项的取值范围是__
__.
20、
对个向量，如果存在不全为零的实数使得，则称线性相关.若已知，，是线性相关的，则=___
_________.
12、若数列是等差数列，则数列也为等差数列；类比上述性质，相应地，若数列是等比数列，且，则有=___
____也是等比数列.
二、选择题（共4小题，每题3分，共12分）
13、下列各式中错误的是…………………………………………………………………（ C ）
A. B.
C. D.
14、已知，为线段的中点，则向量与的夹角是（ A ）
A. B.
C. D.
15、已知等差数列中，，则的值是………………………（ D）
A. B. C. D.
16、在△中，有命题①若，则△为锐角三角形②③,则△为等腰三角形 ④.上述命题正确的是…………………………………………………………………………………………（ C ）
A.①② B. ①④ C. ②③ D. ②③④
四、解答题（共6小题，第17题6分，第18、19、20题每题8分，第21题10分，第22题12分，共52分）
17 已知，且∥，，求点的坐标.
解：设点C 的坐标是
，
则
，
，
……………………2分
由∥
…………………………………………2分
，所以
………………………………………………2分
18 已知一个等差数列的前项的和是，前项的和是.求此等差数列的前项和，并求出当为何值时，最大，最大值是多少？
解：设等差数列的首项为，公差为
……………………………………1分
则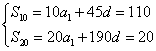 
……………………………………………2分
所以
，
所以
…………………………………………………………2分
又
，
所以当
或
时最大，
……………………3分
19设数列的首项，且（）.（1）求；
（2）根据上述结果猜想数列的通项公式，并用数学归纳法加以证明.
解：（1）
………………………………………………2分
（2）猜想
，（）……………………………………2分
证明：①当
时，左边
，右边
，猜测成立；
②假设当
（
）时有
成立
则当
时，左边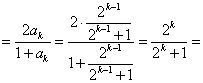
右边.故猜测也成立.
由①②可得对一切，数列的通项公式为 （）…………4分
20、在一次人才招聘会上，有甲、乙两家公司分别公布它们的工资标准：
甲公司：第一年月工资数为1500元，以后每年月工资比上一年月工资增加230元；
乙公司：第一年月工资数为2000元，以后每年月工资在上一年的月工资基础上递增5%.
设某人年初同时被甲、乙公司录取，试问：
（3）
若该人打算连续工作年，则在第年的月工资收入分别是多少元？
（4） 若该人打算连续工作10年，且只考虑工资收入的总量，该人应该选择哪家公司？为什么？(精确到1元)
解：（1）设在甲公司第年的工资收入为
元，在乙公司第年的工资收入为
元
则
，
………………………………4分
（2）设工作10年在甲公司的总收入为
，在甲公司的总收入为
由于
，所以该人应该选择甲公司.…………………………4分
21、已知，分别是与轴，轴正方向相同的单位向量， ，对任意正整数，.
（1）若，求的值；
（2）求向量.
解：（1）依题可知
由知
，所以
；…………………………4分
（2）
…………………………………………2分
所以
.……………………………………4分
22、我们在下面的表格中填写数值：先将第1行的所有空格填上1；再把一个首项为1，公比为的数列依次填入第一列的空格内；然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其他空格.
| 第1列 | 第2列 | 第3列 | …… | 第 | |
| 第1行 | 1 | 1 | 1 | …… | 1 |
| 第2行 |
|
|
|
| |
| 第3行 |
|
| |||
| …… | …… | ||||
| 第 |
|
|
（1）按照填写规则，请在上述表格内填写第二行的空格以及第二列的空格；
（2）试用、表示第二列的各数之和；
（3）设第3列的数依次为，若成等比数列，试求的值；能否找到的值，使得数列的前项 成为等比数列？若能找到，的值有多少个？若不能找到，说明理由.
解：（1）如表……………………………………………………………………3分
（2）
当
时，
；……………………………………2分
当
时，
…………………………………………2分
所以综上可知
……………………1分
（5）
可知
由
，则
若
时，为等比数列，那么一定是等比数列
由上可知此时
，又 
得知
而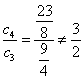
，所以对于任意的
，一定不是等比数列
综上所述，当且仅当
且时，数列是等比数列.………4分