高二年级数学第二学期返校考试
数学试卷(理科)
命题人：史文洁 审题人：徐进光
说明：本试卷满分为100分，考试时间100分钟．学生不得使用计数器。
以下公式或数据供参考:①.
；
②.正态曲线方程：
一．选择题（本大题共10小题，每小题3分，共30分。在每个题给出的四个选项中，有且只有一项是符合题目要求的，请将答案填写在答卷纸上）。
1. 下面一段程序执行后输出结果是 ( )
程序： A=2
A=A*2
A=A+6
PRINT A
A. 2 B.
2.为研究一片经济林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）．根据所得数据画出样本的频率分布直方图，（如右图）那么在这100株树木中，底部周长小于
A.30 B
3. 10名工人某天生产同一零件，生产的件数是5，7，4，
10，5，7，7，6，4，2，设其平均数为a，中位数为
b，众数为c，则有（ ）
A．
B．
C．
D．
4．两位同学一起去一家单位应聘，面试前单位负责人对他们说：“我们要从面试的人中招聘3人，你们俩同时被招聘进来的概率是
”．根据这位负责人的话可以推断出参加面试的人数为（ ）
A．21 B．
5.正态分布
，则
约等于（ ）
A.
B.
C.
D.
6.有
件不同的产品排成一排，若其中
两件产品必须排在一起的不同排法
有48种，则
的值为（ ）
A.4 B.5 C.6 D.7
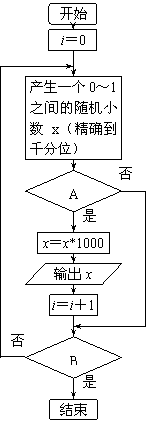
7.从1到815这815个整数中选出100个整数（一个整数可以重复被选），现在利用电脑模拟随机数抽样，程序框图如右图所示，则在A、B两框中应填入（ ）
A．
B．
C．
D．
8．从装有两个红球和两个黑球的口袋里任取两个球，那么互斥而不对立的两个事件是（ ）
A．“至少有一个黑球”与“都是黑球”
B．“至少有一个黑球” 与“至少有一个红球”
C．“恰好有一个黑球”与“恰好有两个黑球”
D．“至少有一个黑球”与“都是红球”
9．设集合
，分别从集合
和
中随机取一个数
和
，确定平面上的一个点
，
记“点落在直线 
上”为事件
，若事件
的概率最大，则
的所有可能值为（ ）
A. 3 B.4 C. 2和5 D.3和4
10. 某一施工单位买了一条长度为12米的直线型钢管，两端用字母A、B表示，由于施工需要，在中间钻两个孔C、D,次序为A、C、D、B，则A与C，B与D之间的距离都不小于4米的概率为（ ）
A．
B．
C．
D．
二、填空题（共7小题，每小题3分,共21分，把答案填在答题卷上）
11.随机变量
服从二项分布～
，且
则
=__________
12．将数
转化为十进制数为______________
13．如图， A, B, C表示3种开关，设在某段时间内它们正常工作的概率是分别是0.9 , 0.8 , 0.7 , 如果系统中至少有1个开关能正常工作, 那么该系统正常工作的概率是
14．
的展开式中，
的系数是 .
15. 若随机变量
服从两点分布，且
，
．令
，则
．
16．若
的展开式中第10项的二项式系数最大，则n的值_____________。
17．一种电脑屏幕保护画面，只有符号“○”和“×”，随机地反复地出，每秒钟变化一次，每次变化只出现“○”和“×”之一，其中出现“○”和“×”的概率都为
，若第k次出现“○”， 则记
，出现“×”，则记
，令
，则
的概率为 ．
三、解答题（共5题，第18、19题各8分，第20、21、22、小题各11分）
18.用辗转相除法求840与1764的最大公约数.
|
| 2 | 3 | 4 | 5 | 6 |
|
| 2 | 4 | 7 | 10 | 12 |
19．假设关于某设备使用年限x（年）和所支出的维修费用y（万元）有如下统计资料：若由资料知，y对x呈线性相关关系，试求：
（1）回归直线方程；
（2）估计使用年限为10年时，维修费用约是多少？
20．有4个不同的球，四个不同的盒子，把球全部放入盒内．试求：
（1）共有多少种不同的放法？
（2）若恰有一个盒不放球，共有多少种不同的放法？
（3）若恰有两个盒不放球，共有多少种不同的放法？
21．两个三口之家（四个父母亲，两个小孩）出去旅游．
（1）分坐编号为A、B、C的三只小船过河，规定：每两人坐一只船，两个小孩不能坐一只船，有几种坐法？
（2）6人排队入景点游玩，小孩不能站头尾且与他的母亲相邻，这6人有几种排队方法。
22．在一个盒子中，放有标号分别为1，2，3，4的四张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x、y，记X＝x－2＋y－x．
（1）求随机变量X的最大值，并求事件“X取得最大值”的概率；
（2）求随机变量X的分布列和均值．
（3）在
的条件下，求
的概率。