高二数学同步测试

直线与圆锥曲线（八）

一、选择题

1.（2004年全国·理7）椭圆的两个焦点为F₁、F₂，过F₁作垂直于x轴的直线与椭圆相交，一个交点为P，则=　　　 （  　 ）

　　　 A．　　　　　　  B．　　　　　　 C．　　　　　　 D．4

2（2004年全国·理8）设抛物线y²=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是（　　 ）

　　　 A．[－，]　　 B．[－2，2]　C．[－1，1]　D．[－4，4]

3.（2004年全国·理4）已知圆C与圆关于直线对称，则圆C的方程为（ 　　）

　　　 A．　　　 B．

　　　 C．　 D．

4.（2004年全国·文8）已知点A（1，2）、B（3，1），则线段AB的垂直平分线的方程是（　）

　　　 A．　　 B．　　 C．　　 D．

5.（2004年全国·理8）在坐标平面内，与点A（1，2）距离为1，且与点B（3，1）距离为2的直线共有（　　 ）

　　　 　A．1条　　　　B．2条　　　　C．3条　　　　D．4条

6.（2004年全国·理9）已知平面上直线l的方向向量e=点O（0，0）和A（1，－2）在l上的射影分别是O′和A′，则e，其中=（　 　）

　　　 A．　 　 B．　　　C．2　　　 　D．－2

7.（2004年全国·理1）设集合，，则集合中元素的个数为（　　 ）

　　　 　　　 A．1　　　　　　　 B．2 　　　　　　　C．3　　　　 　　 D．4

8.（2004年全国·理4）圆在点处的切线方程为（　　）

　　　 A．　 　　 B．　

　　　 C．　　　　 D．

9.（2004年全国·理7）设双曲线的焦点在轴上，两条渐近线为，则该双曲线的离心率（ 　　）

　　　 A．　　　　 B． 　　　　　　C．　　  　　 D．

10.（2004年全国理3）过点（－1，3）且垂直于直线的直线方程为（ ）

　　　 A．　　　　　　　B．

　　　 C．　　　　　　 D．

11.（2004年全国文7）已知函数的图象有公共点A，且点A的横坐标为2，则（ 　　）

　　　 A． 　　 B．　 　　　C ．　 　　　　D．

二、填空题

12.（2004年全国·理14）由动点P向圆x²+y²=1引两条切线PA、PB，切点分别为A、B，∠APB=60°，则动点P的轨迹方程为　　　　　　　　　  .

13.（2004年全国文16）设P为圆上的动点，则点P到直线的距离的最小值为　　　　　　　 .

14.（2004年全国·理16）设是曲线上的一个动点，则点到点的距离与点到轴的距离之和的最小值为　　　　　　 .  　　　　　　

15.（2004年湖南高考·文史类第15题）F₁，F₂是椭圆C：的焦点，在C上满足PF₁⊥PF₂的点P的个数为__________.

16.（2004年湖南高考·理工类第16题）设F是椭圆的右焦点，且椭圆上至少有21个不同的点P_i（i=1，2，3，…），使FP₁，FP₂，FP₃，…组成公差为d的等差数列，则d的取值范围为　　　　　　 .

三、解答题

17.已知抛物线的焦点为，过作两条互相垂直的弦、，设、的中点分别为.

  （１） 求证：直线必过定点;

（２）分别以和为直径作圆，求两圆相交弦中点的轨迹方程．

18设是单位圆的直径，是圆上的动点，过点的切线与过点的切线分别交于两点. 四边形的对角线和的交点为，求的轨迹．

19.椭圆的两焦点分别为、，直线是椭圆的一条准线．

（1）求椭圆的方程；

（2）设点在椭圆上，且，求的最大值和最小值．

　　　

20.已知A（－2，0），B（2，0），动点P与A、B两点连线的斜率分别为和，且满足·=t (t≠0且t≠－1).

（１）求动点P的轨迹C的方程；

（２）当t＜0时，曲线C的两焦点为F₁，F₂，若曲线C上存在点Q使得∠F₁QF₂=120^O，

求t的取值范围．

　　　 .

直线与圆锥曲线（八）参考答案

一、选择题

1.C 　2.C 　3.C 　4.B 　 5.B　　6. D　 7. B 　8.D 　 9.C　 10.A 　11.A

二、填空题

12.x² + y² = 4 　　 13.1　　  14.　　 15.2　　　16.

三、解答题

17.解：（１）由题可知，设，，直线AB的方程为，　　　　　　　　　　　　　　　　　　 

则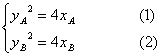

（1）—（2）得，即，代入方程，解得

同理可得：的坐标为.　　　　　　　　　　 

直线的斜率为，方程为，

整理得,

显然，不论为何值，均满足方程，

所以直线恒过定点 .　　　　　　　　　　　　　　 

（２）过作准线的垂线，垂足分别为. 由抛物线的性质不难知道：准线为圆与圆的公切线.

设两圆的相交弦交公切线于点，则由平面几何的知识可知：为的中点. 所以

，

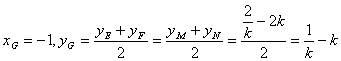即　　.　　　　　　　　　　　　　　　　 

又因为公共弦必与两圆的连心线垂直，所以公共弦的斜率为

,

所以，公共弦所在直线的方程为　,

即　　　 ,　　　　　　　　　　　　　　　　

所以公共弦恒过原点.　　　　　　　　　　　　　　　　 

根据平面几何的知识知道：公共弦中点就是公共弦与两圆连心线的交点，所以原点、定点、所求点构成以为直角顶点的直角三角形，即在以为直径的圆上．

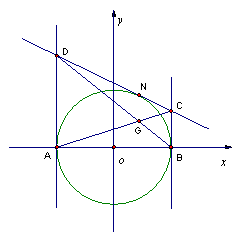
18.解：以圆心O为原点，直径为x轴建立直角坐标系，则A（－1，0），B（1，0），单位圆的方程为设　N的坐标为，则切线DC的方程为：，　　　　　　　　　

由此可得　

AC的方程为　

BD的方程为　

将两式相乘得：，

即

当点N恰为A或B时，四边形变为线段AB，这不符合题意，所以轨迹不能包括A、B两点，所以的轨迹方程为，（）．

19.解：（１）设椭圆的方程为，则由

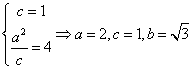，椭圆方程为．

（２）因为在椭圆上，故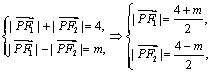

．

由平面几何知识，即，所以．　　　
记，设且，则

，

所以在上单调递减，于是，当时原式取最大值，当时，原式取最小值．

20. 解：(１) 设点P坐标为(x,y),依题意得=ty²=t(x²－4)+=1

轨迹C的方程为+=1（x≠2）.

(２) 当－1＜t＜0时，曲线C为焦点在x轴上的椭圆，

设=r₁，= r₂, 则r₁+ r₂=2a=4.

在△F₁PF₂中，=2c=4,

∵∠F₁PF₂=120^O，由余弦定理，

得4c²=r+r－2r₁r₂= r+r+ r₁r₂

= (r₁+r₂)²－r₁r₂≥(r₁+r₂)²－()²=3a², ∴16（1+t）≥12, ∴t≥－.

所以当－≤t＜0时，曲线上存在点Q使∠F₁QF₂=120^O

当t＜－1时，曲线C为焦点在y轴上的椭圆，

设=r₁，= r₂，则r₁+r₂=2a=－4 t,

在△F₁PF₂中， =2c=4.

∵∠F₁PF₂=120^O，由余弦定理，得

4c²=r+r－2r₁r₂= r+r+ r₁r₂= (r₁+r₂)²－r₁r₂≥(r₁+r₂)²－()²=3a²,

∴16（－1－t）≥－12tt≤－4.

所以当t≤－4时，曲线上存在点Q使∠F₁QF₂=120^O

综上知当t＜0时，曲线上存在点Q使∠AQB=120^O的t的取值范围是