_____班； 姓名_______________ 湖南省省级示范性高中……洞口三中数学测验试卷
___考室;考号_______________号 高二中考 (测试内容：立体几何；排列、组合、二项式定理；概率)
撰稿： 方锦昌 电子邮箱 fangjingchang2 或@.com 手机号码
一、 选择题（5×10=50分）
1、一条直线，与一个平面的一条斜线在这个平面内的射影垂直，是这条直线与这条斜线垂直的：
A.充分不必要条件； B.必要不充分条件； C.充要条件； D.既不充分又不必要条件
2、数
除以7之后所得的余数是：
A. 0； B. 1； C. 2； D 6
3、甲、乙两人独立地解决同一数学问题，甲能解决该问题的概率是0.8，乙能解决该问题的概率是
0.6,那么甲、乙两人中至少有一个人可解决这个问题的概率是：
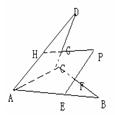
4、已知E、F、G、H依次为空间四边形ABCD的边AB、BC、CD、DA上的点，且直线EF交直线HG于点P，则点P的位置是必处在( )的上面：
A、 BD B、AD C、AC D 、平面BCD之内
5．在平行六面体ABCD—A1B
，则x＋y＋z等于： A．1 B． C． D．
6、位于坐标原点的一个质点
按下列规则移动：质点每次移动一个单位；移动的方向为向上或向右，并且向上、向右移动的概率都是
，则质点移动五次后位`于点
的概率是：
（A） ()5 （B） C25 ()5 （C）C35()3 （D）C25C35()5
7 .若在二项式
的展开式中任取一项，则该项的系数为奇数的概率为：
(A) 
(B) 
(C) 
(D)
8．用0，1，2，3，4这五个数字组成无重复数字的五位数，要求奇数数字相邻，偶数数字也相邻，
这样的数共有多少个：（A）20个 （B）24个 （C）32个 (D)36个
9．在
的展开式中含有常数项，则正整数n的最小值是：
（A）4 (B) 5 (C) 6 (D) 7
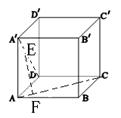
10．如图，在正方体ABCD—A′B′C′D′中，EF是异面直线AC与A′D的公垂线,
则由正方体的八个顶点所连接的直线中,与EF平行的直线：
A 有且只有一条 B 有二条 C 有四条 D 不存在
二、填空题（5×5=25分）：
11、若
，
则
12、洞口三中欲安排蒋老师、杨老师等七位老师在
13、在
展开式中第9项为常数，则n的值为
14．有一块三角板ABC，
，
，
边是贴于桌面上的，当三角板与桌面成
时，
则AB边与桌面所成的角的正弦值是 。
15．已知m、n是直线，α、β、γ是平面，给出下列命题：
①若α⊥β，α∩β=m，n⊥m ，则n⊥α或n⊥β；②若α∥β，α∩γ=m，β∩γ=n，则m∥n；
③若m不垂直于α，则m不可能垂直于α内的无数条直线；④若α∩β=m，n∥m，且nËα，nËβ，
则n∥α且n∥β．其中正确的命题序号是 ________(注：把你认为正确的命题的序号都填上)
（一）、选择题答案
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
（二）、填空题答案：11题____________； 12题____________； 13题_______________；
14题____________________； 15题____________________；
三、 解答题(75分)：
16、（3+3+3+3=12分）中考后,洞口三中288班要从5名男生中，3 名女生中选出5人担任5门不同学科的课代表，请分别求出满足下列条件的方法数目：
①、所安排的女生人数必须少于男生 ；
②、其中的女生王丽丽指定是担任语文课代表的；
③、其中的男生付勇波必须是课代表，但又不能担任数学课代表；
④、女生王丽丽必须担任语文课代表，且男生付勇波必须担任课代表，但又不担任数学课代表。
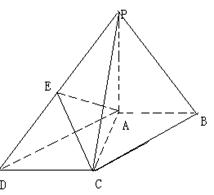17．（4+4+4=12分）如图，在底面为平行四边形的四棱锥
中，
，
平面
，且
，点
是
的中点.
（Ⅰ）求证：
；
（Ⅱ）求证：
平面
（Ⅲ）求二面角
的大小.
18题．（ 6+6=12分）洞口三中本届高三即将毕业的学生罗奕同学,学习踏实,成绩拨尖,据现有的情况分析预测,她在今年六月的高考中,语、数、英三科成绩，夺取全县第一的概率：语文可达0.9，数学可达0.8，英语可达0.85，据此,请你估测:在今年的高考中：
（1）罗奕同学三科成绩均未能夺得全县第一的概率是多少？
（2）罗奕同学恰有一科成绩未夺得全县第一的概率是多少？
19题．（6+6=12分）已知()n展开式中的倒数第三项的系数为45，
求：⑴写出其展开式中含x3的项；
⑵写出其展开式中系数最大的项．
20(7+7=14分)．美国NBA篮球总决赛采用七局四胜制,即先胜四局的队获胜,比赛结束。2007年美国东部活塞队与西部马刺队分别进入总决赛,已知马刺队与活塞队的实力相当,即单局比赛每队获胜的概率均为；若第一场比赛组织者可获门票收入30万美元,以后每一场门票收入都比上一场增加10万美元，设各局比赛相互之间没有影响.
①、求组织者在本次比赛中获门票收入为180万美元的概率；
②、若组织者在本次比赛中获门票收入不低于330万美元，其概率为多少.
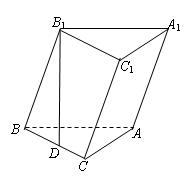
21．(4+4+5=13分)已知斜三棱柱ABC—A1B
为α (0°＜α＜90°)，点
在底面上的射影
落在上．
(1)求证：AC⊥平面BB
(2)若AB1⊥BC1，D为BC的中点，求α ；
(3)若α = arccos ，且AC=BC=AA1时，求二面角C1—AB—C的大小．
高二中考数学参考答案
（一）、选择题答案
| 题次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | D | C | D | B | C | A | B | A |
（二）、填空题答案：
11题：129； 12题：2400种； 13题：12；
14题：
； 15题：(2)(4)；
(三)、解答题
16题、解：①依题意得：
；
②依题意得：
③依题意得：
④依题意得：
17题．解：（1）由平面可得PA^AC;又，所以AC^平面PAB，所以;
（2）如图，连BD交AC于点O，连EO，则EO是△PDB的中位线，\EO
PB;\PB
平面;
（3）如图，取AD的中点F，连EF，FO，则EF是△PAD的中位线，\EFPA又平面，\EF^平面;同理FO是△ADC的中位线，\FOAB\FO^AC由三垂线定理可知\ÐEOF是二面角E－AC－D的平面角.又FO＝AB＝PA＝EF\ÐEOF＝45°而二面角与二面角E－AC－D互补，故所求二面角的大小为135°.
18题：解:分别记语、数、英考试成绩排名全县第一的事件为A、B、C，则P(A)=0.9，P(B)=0.8，P(C)=0.85．
(1)、三科成绩均未获得第一名的概率是
=[1-P(A)]·[1-P(B)]·[1-P(C)]=(1-0.9)×(1-0.8)×(1-0.85) =0.003
(2)、恰有一科成绩未获得第一名的概率是P(
)= P(
=
=(1-0.9)×0.8×0.85+0.9×(1-0.8)×0.85+0.9×0.8×(1-0.85)=0.329．
19．解：⑴由题设知
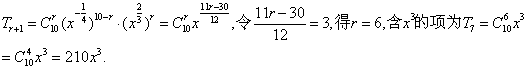
⑵系数最大的项为中间项，即
20． 解:(Ⅰ)、每场比赛的门票收入构成等差数列｛an｝,其中a1=30，d=10，则an=20+10n,Sn=25n+5n2,由Sn=180得n=4(n=-9舍去），即比赛进行4场，∴P4=
(Ⅱ)、由Sn≥330，则n≥6(n≤-11舍去），则必须比赛6或7场：
(1)、比赛6场的概率为P6=C12C35（）5×（）；
(2)、比赛7场的概率为P7=C12C36（）5×（）；
∴P求= P6+P7=
21题:解 (1)∵
B1D⊥平面ABC， AC
平面ABC，∴ B1D⊥AC， 又AC⊥BC，
BC∩B1D=D．
∴ AC⊥平面BB
(2) ∵ AC⊥平面BB
∴ 平行四边形BB
∴△BB
(3)过C1作C1E⊥BC于E，则C1E⊥平面ABC．过E作EF⊥AB于F，C
∴∠C1FE是所求二面角C1—AB—C的平面角．设AC=BC=AA1=a，
在Rt△CC1E中，由∠C1BE=α=
，C1E=
a．在Rt△BEF中，∠EBF=45°，EF=
BE=a．
∴∠C1FE=45°，故所求的二面角C1—AB—C为45°．
解法二：(1)同解法一 ；
(2)要使AB1⊥BC1，D是BC的中点，即
=0，=，∴
， 
=0，∴
．∴
，故△BB
(3)以C为原点，CA为x轴，CB为y轴，经过C点且垂直于平面ABC的直线为z轴建立空间直角坐标系，则A(a，0，0)，B(0，a，0)，C(0，-
，a)，平面ABC的法向量n1=(0，0，1)，设平面ABC1的法向量n2=(x，y，z)．由
n2=0，及
n2=0，得
∴n2=(
，，1)．cos＜n1， n2＞= = ，
故n1 ， n2所成的角为45°，即所求的二面角为45°