高二下学期数学期中考试试卷

数　学（理 科 ）　　

第一部分　选择题（共40分）时间: 120分钟  满分:150分

一.选择题：本大题共8小题，每小题5分，共40分．(每小题给出的四个选项中，有且仅有一个是符合题意，选错，不选，多选或涂改不清的均不给分．)

1.复数在复平面内对应的点位于（　　）

　 (A) 第一象限　　(B) 第二象限　　(C) 第三象限　　(D) 第四象限

2．函数的导数为(　　　)

A. 　　　　　B.

　C. 　　　　　　 D.

3.“因指数函数是增函数（大前提），而是指数函数（小前提），所以是增函数（结论）”，上面推理的错误是（ 　）。

 （A）大前提错导致结论错　　　　　 （B）小前提错导致结论错　

（C）推理形式错导致结论错　　　　 （D）大前提和小前提错都导致结论错

4.如果命题对成立，则它对也成立，若对成立，则下列结论正确的是（　　　）

A. 对一切正整数都成立；　　B. 对任何正偶数都成立；

C. _{对任何正奇数都成立；}　　D. _{对所有大于1的正整数都成立。}

5．的值为(　　　)

A. 　　　　　　　B. 　　　　　　　 C. 　　　　　　D.

6．已知命题，则是（　 ）

　　　 A．　　 B．

　　　 C．　　　　　　　　　　　　　　　　　D．

7．函数的单调增区间为　　　　　　（　　）

　　A．（－2，3）　　　　　　　　　　B．（―∞，―2）和（－2，3）

　　C．（－2，3）和（3，+∞）　　　　D．（－∞，－2）和（3，+∞）

8．已知是定义在R上的增函数，且,则函数的单调情况一定是(　　 )

　(A) 在(-∞，0)上递增　　 （B）在(-∞，0)上递减　

 （C）在R上递增　　　　　 （D）在R上递减

第二部分 非选择题（共110分）

二.填空题：本大题共6小题，每小题5分，满分30分.

9.复数的共轭复数是　　　 。

10.函数y=2x-x² ,x∈[0,2]的最大值是 　　　　　　　。

11.双曲线的离心率为：　　　 。

12.设向量　　

13．已知=__________.

14．在曲线的切线中斜率最小的切线方程

是____________________.

三.解答题：本大题共6小题，共80分．解答应写出文字说明、演算步骤或推证过程.

15. （本小题满分12分）计算下列函数的导数和定积分。

（1）　 　　　　　　　　（2）

16．（本小题满分12分）已知抛物线与直线

（Ⅰ）求两曲线的交点；

（Ⅱ）求抛物线在交点处的切线方程．

17．（本小题满分14分）已知a为实数，.

 （1）求导数；

 （2）若函数在处取得极值，求在上的最大值和最小值.

18. （本小题满分14分）求曲线，所围成的面积。

19.（本小题满分14分）

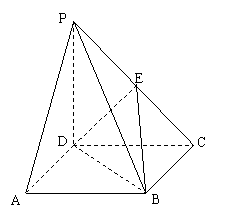　如图，在四棱锥P—ABCD中，底面ABCD是

正方形，侧棱PD⊥底面ABCD，PD=DC,点E是PC的中点．

F

作EF⊥PB交PB于点F。

 （1）证明：PA //平面EDB；

（2）证明：PB⊥平面EFD．

（3）求二面角C－PB－D的大小。

20. （本小题满分14分）　已知三点P（5，2）、（－6，0）、（6，0）.

　　 （Ⅰ）求以、为焦点且过点P的椭圆的标准方程；

（Ⅱ）设点P、、关于直线y＝x的对称点分别为、、，求以、为焦点且过点的双曲线的标准方程。