直线的方程
A卷
一、选择题
1、如果ab＞0，bc＞0，那么直线ax－by－c = 0必经过( )
A、一、二、三象限 B、一、二、四象限
C、一、三、四象限 D、二、三、四象限
2、直线ax + by－1 = 0的倾斜角是直线
的斜角的2倍，且它在y轴上的截距为1，则a，b为( )
A、a =
3、直线
，在y轴上的截距为( )
A、 b B、±b C、b2 D、－b2
4、已知直线在两轴上的截距之和是2，并且经过(－2，3 ) ，则直线方程为( )
A、3x－2y + 12 = 0 B、x + y－1 = 0
C、x－2y + 4 = 0或3x + y－3 = 0 D、2y－3x－12 = 0或y = 1－x
5、经过点A(1，2 )，并且在两坐标轴上的截距的绝对值相等的直线共有( )
A、1条 B、2条 C、3条 D、4条
6、下列四个命题中真命题是( )
A、经过定点(x0，y0 )的直线都可以用方程y－y0 = k(x－x0 )表示
B、经过任意两个不同的点P1(x1，y1 )、P2(x2，y2 )的直线都可以用方程(y－y1 ) (x2－x1 ) = (x－x1) (y2－y1 )表示
C、不经过原点的直线可以用方程
表示
D、经过定点A(0，b )的直线都可以用方程y = kx + b表示
二、填空题
7、过点P(1，2 )且在两坐标轴上截距和为0的直线方程为 。
8、过点P(1，2 )并且与x轴平行的直线方程是 。
9、如果直线l的点斜式方程为
，则l经过点
，其斜率为
。
10、已知直线l在x轴上截距比在y轴上的截距大1，且过定点(6，－2 )，则直线l的方程为 。
11、已知P(3，m )在过M(2，－1)和N(－3，4)的直线上，则m的值是 。
12、若直线l1的斜率为k1，倾斜角为 
,直线l2的斜率为k2，倾斜角
，且k1 + k2 = 0，(k1, k2≠0)则+ = 。
13、斜率为2的直线过(3，5)、(a，7)、(－1，b)三点，则a = ，b = 。
14、直线ax + 3y －5 = 0过以(－1，－2)、(2，4)为端点的线段的中点，则a = 。
15、若直线的倾斜角为
，且过点(1，0)，则直线l的方程为 。
16、已知直线x－2y + 2k = 0与两坐标轴围成的三角形的面积不大于1，则实数k的取值范围是 。
17、原点在l上的射影是点P(－2，1)，则直线l的方程是 。
18、过点P(－2，4)且平行于直线2x－3y + 1 = 0的直线方程为 。
19、与直线l1：x－y +
= 0关于原点成中心对称的直线l2的方程是
。
三、解答题
20、△ABC的三个顶点为A(0，4)、B(－2，6)、C(8，2)，求此三角形各边上的中线所在直线的方程。
21、求经过点(－5，5)且和原点距离是1的直线方程。
直线的方程 B卷
一、综合题
1、过原点的两条直线把直线2x + 3y－12 = 0的坐标轴间的线段分成三等份，求这两条直线的方程。
2、已知两点A(1，1 )、B(2，3 )和直线l：3x－y = 0，在直线l上求一点P，使 PA 2 +
PB 2最小，并求出最小值。
3、求证：不论m取何实数，直线(2m－1)x－(m + 3)y－(m－11) = 0恒地一个定点，并求出此定点的坐标。
4、过点A(0，1)作直线l，使它夹在直线l1：x－3y + 10 = 0和l2：2x + y－8 = 0间的线段被A点平分，求直线l的方程 。
二、应用题
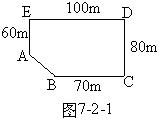
5、某房地产公司要在荒地ABCDE上划出一块长方形地面(不改变方位)建造一幢8层楼的公寓如图7-2-1所示，问如何设计才能使公寓占地面积最大？并求出最大面积(精确到1m2).
 |
三、应用题
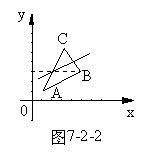6、已知三点：A(1，1)，B(5，3)，C(4，5)，又直线l∥AB，且l平分△ABC的面积如图7-2-2所示，求直线l的方程。
四、高考题
7、l1：y = x，l2：ax－y = 0，其中a为实数，当这两条直线的夹角
内变动时，a的取值范围是( )
A、(0，1) B、
C、
D、
8、设动点P在直线x = 1上，O为坐标原点，以OP为直角边，点O为直角顶点作等腰Rt△OPQ，则动点Q的轨迹是( )
A、圆 B、两条平行直线 C、抛物线 D、双曲线
9、如果直线l沿x轴负方向平移3个单位，再沿y轴正方向平移一个单位后，又回到原点的位置，则直线l的倾斜角是 。
参考答案
一、选择题
1、C 2、A 3、D 4、D 5、C 6、B
二、填空题
7、x－y + 1 = 0或y =
2x
8、y = 2 9、
10、
11、－2
12、π 13、4，－3
14、4 15、x + 2y－1= 0 16、－1≤k≤1 17、2x－y + 5 = 0
18、2x－3y + 16 = 0 19、
三、解答题
20、
21、4x + 3y + 5 = 0和3x + 4y－5 = 0
B卷
一、综合题
1、
2、
，最小值为
3、解：将方程化为
，
它表示过两直线
的交点的直线系。
解方程组
∴直线恒过(2,3)点
4、
二、应用题
5、
时，公寓面积最大为
三、创新题
6、
四、高考题
7、C 8、B 9、
