高二数学期末复习测试题二（直线与圆的方程）

一、选择题

1．点P分有向线段的比为，则点B分有向线段的比为（　　）

A．　　　　　　　　　　　　 B．　　　　　　　　　　　　　C．-　　　　　　　　 D．-

2．直线y=xcosα+1(α∈R)的倾斜角的取值范围是（　　）

A．[0，]　　　　　　　　　　　　　　　 B．[0，π

C．[-，]　　　　　　　　　　　　　　D．[0，]∪[，π

3．若圆x²+y²-ax-2y+1=0关于直线x-y-1=0对称的圆的方程是x²+y²-4x+3=0，则a的值等于（　　）

A．0　　　　　　　　　　　　　　B．1　　　　　　　　　　　　　　C．2　　　　　　　　　　　　　　D．±2

4．点M(x₀,y₀)是圆x²+y²=a² (a>0)内不为圆心的一点，则直线x₀x+y₀y=a²与该圆的位置关系是（　　）

A．相切　　　　　　　　　　　B．相交　　　　　　　　　　　 C．相离　　　　　　　　　　　D．相切或相交

5．圆x²+2x+y²+4y-3=0上到直线x+y+1=0的距离为的点共有（　　）

A．1个　　　　　　　　　　　 B．2个　　　　　　　　　　　　C．3个　　　　　　　　　　　 D．4个

6．直线x+y-1=0沿y轴正方向平移1个单位再关于原点对称后，所得直线的方程是（　　）

A．x+y+2=0　　　　　　　　B．x-y-2=0　　　　　　　　　C．x+y-2=0　　　　　　　　 D．x-y+2=0

7．已知两点A(-2,0),B(0,2)，点C是圆x²+y²-2x=0上的任意一点，则△ABC的面积最小值是（　　）

A．3-　　　　　　　　　　B．3+　　　　　　　　　　C．　　　　　　　　 D．

8．已知三条直线l₁：y=x-1, l₂：y=1, l₃：x+y+1=0。设l₁与l₂的夹角为α，l₁与l₃的夹角为β，则α+β等于（　　）

A．45°　　　　　　　　　　　B．75°　　　　　　　　　　　 C．105°　　　　　　　　　　 D．135°

9．直线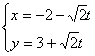（t为参数）上到点A(-2,3)的距离等于的一个点的坐标是（　　）

A．(-2,3)　　　　　　　　　　　　　　B．(-4,5)　　　　　　　　　　　　　　C．(-2-,3+)　　　　　　D．(-3,4)

10．将直线x+y=1绕(1,0)点顺时针旋转90°后，再向上平移1个单位与圆x²+(y-1)²=r²相切，则r的值是(　　)

A．　　　　　　　　　　　B．　　　　　　　　　　　 C．　　　　　　　　　　 D．1

11．若曲线x²+y²+a²x+(1-a²)y-4=0关于直线y-x=0对称的图形仍是其本身，则实数a=(　　)

A．±　　　　　　　　　　　B．±　　　　　　　　　 C．或-　　　　　　　D．-或

12．若圆(x-1)²+(y+1)²=R²上有仅有两个点到直线4x+3y=11的距离等于1，则半径R的取值范围是（　　）

A．R>1　　　　　　　　　　　 B．R<3　　　　　　　　 　　　 C．1<R<3　　　　　　　　　　D．R≠2

二、填空题

13．圆心在直线y=x上且与x轴相切于点(1,0)的圆的方程为　　　　　 。

14．A点是圆C：x²+y²+ax+4y-5=0上任意一点，A点关于直线x+2y-1=0的对称点也在圆C上，则实数a=　　　　　　　 　　　 。

15.过点M（0，4），被圆(x-1)²+y²=4截得的线段长为2的直线方程为　　　　。

16.已知两点M(0,1),N(10,1)，给出下列直线方程

①5x-3y-22=0;②5x-3y-52=0;③x-y-4=0;④4x-y-14=0。在直线上存在点P满足MP=NP+6的所有直线方程的序号是　　　　　　　　　  。

三、解答题

17．直线l过点P(2,1)，按下列条件求直线l的方程

（1）直线l与直线x-y+1=0的夹角为；

（2）直线l与两坐标轴正向围成三角形面积为4。

18．求经过点A(4,-1)，并且与圆x²+y²+2x-6y+5=0相切于点M(1,2)的圆方程。

19．已知曲线C：x²+y²-2x-4y+m=0

（1）当m为何值时，曲线C表示圆；

（2）若曲线C与直线x+2y-4=0交于M、N两点，且OM⊥ON(O为坐标原点)，求m的值。

20．如图9-6，已知点A、B的坐标分别是（-3，0），（3，0），点C为线段AB上任一点，P、Q分别以AC和BC为直径的两圆O₁，O₂的外公切线的切点，求线段PQ的中点的轨迹方程。

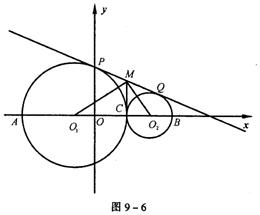
21．如图9-7，已知圆C：x²+y²=4,A(,0)是圆内一点。Q是圆上一动点，AQ的垂直平分线交OQ于P，当点Q在圆C上运动一周时，点P的轨迹为曲线E。

（1）求曲线E的方程；

（2）过点O作倾斜角为θ的直线与曲线E交于B₁、B₂两点，当θ在范围（0，）内变化时，求△AB₁B₂的面积S(θ)的最大值。

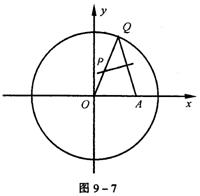
22．已知双曲线C₁和椭圆C₂： +=1有公共的焦点，它们的离心率分别是e₁和e₂,且+=2。

（1）求双曲线C₁的方程；

（2）圆D经过双曲线C₁的两焦点，且与x轴有两个交点，这两个交点间的距离等于8，求圆D的方程。

高二数学期末复习测试体二（直线与圆的方程）参考答案

一、选择题

1.C  2.D　3.C　4.C  5.C　6.A　7.A  8.D　9.D　10.A　11.B　12.C

二、填空题

13.(x-1) ² +(y-1) ²=1　14.-10　15.x=0或15x+8y-32=0　16.②,③

三、解答题

17.（1）利用夹角公式求得直线l的斜率k=或，所求直线l的方程为

或。

（2）易得x+2y-4=0。

18.解　圆x²+y²+2x-6y+5=0的圆心为C(-1,3),设所求圆的圆心为O(a,b)，半径为r。AM的中垂线方程为x-y-2=0 ①，直线MC的方程为：x+2y-5=0　②,

解①、②得圆心O(a,b)的坐标是O(3，1),半径r=OM=，

故所求圆方程为(x-3)²+(y-1)²=5。

19.解 （1）由D²+E²-4F=4+16-4m=20-4m>0，得m<5。

（2）设M(x₁,y₁),N(x₂,y₂)，由OM⊥ON得x₁x₂+ y₁y₂=0。

将直线方程x+2y-4=0与曲线C：x²+y²-2x-4y+m=0联立并消去y得

5x²-8x+4m-16=0，由韦达定理得x₁+x₂=①,x₁x₂=②，又由x+2y-4=0得y= (4-x), ∴x₁x₂+y₁y₂=x₁x₂+(4-x₁)· (4-x₂)= x₁x₂-( x₁+x₂)+4=0。将①、②代入得m=.

20.解　 作MC⊥AB交PQ于点M，则MC是两圆的公切线，∴MC=MQ，MC=MP，即M为PQ的中点。设M(x,y)，则点C，O₁，O₂的坐标分别是(x,0),( ,0)（，0）。连O₁M，O₂M，由平几知识得：∠O₁MO₂=90°，

∴有O₁M²+O₂M²=O₁O₂²，即：

(x-)²+y²+(x-)²+y²=(-)²,化简得x²+4y²=9。又∵点C(x,0)在线段AB上，且AC， BC是圆的直径，∴-3<x<3。

故所求的轨迹方程为x²+4y²=9(-3<x<3)。

21.解　（1）∵P在AQ的垂直平分线上，又在半径OQ上，∴PQ=PA，且OP+PA=OQ=2，

故P点的轨迹是以O、A为焦点，长轴长为2，中心在（，0）的椭圆：

(x-)²+=1

（2）设OB₁=x，则AB₁=2-x，在△OAB₁中，由余弦定理得AB₁²=OB₁²+OA²-2OB₁·OA

cosθ，

即(2-x)²=x²+3-2x·cosθ，解得x=,

同理可得,

S(θ)=S=S+S

=OA·OB₁sinθ+OA·OB₂sin(π-θ)

=OA(+)

==≤

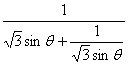当且仅当sinθ=，即θ=arcsin时取等号，

∴当θ=arcsin时，S_max(θ)=。

22.解 （1）椭圆C₂的两个焦点坐标为F₁(-7,1)，F₂(3,1)，离心率e₂=。

由+=2可知双曲线C₁的离心率e₁=,

∴c²=25，a²=9,b²=c² – a²=16,

故双曲线C₁的的方程为-=1。

（2）∵圆D经过双曲线的两个焦点，∴圆心D在直线x= -2上。

设圆D的方程为(x+2)²+(y-b)²=5²+(b-1)²,整理得：x²+y²+4x-2by+2b-22=0，

令y=0，得x²+4x+2b-22=0。

设圆D与x轴的两个交点为(x₁,0),(x₂,0)，则x₁+x₂= -4,x₁x₂=2b-22。

依题意x₁-x₂==8，

即16 - 4(2b-22)=64，解得b=5。 所以圆的方程为(x+2)²+(y-5)²=41。