高中学生学科素质训练
新课标高二数学同步测试(1)(必修5第三章)
说明:本试卷分第一卷和第二卷两部分,第一卷50分,第二卷100分,共150分;答题时间120分钟。
第Ⅰ卷(选择题共50分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.若a<b,d<c,并且(c-a)(c-b)<0,(d-a)(d-b)>0,则a、b、c、d的大小关系是 ( )
A.d<a<c<b B.a<c<b<d C.a<d<b<c D.a<d<c<b
2.若实数a、b满足a+b=2,是
A.18 B.![]() D.2
D.2![]()
3.![]() 在
在![]() 上满足
上满足![]() ,则
,则![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.若关于![]() 的方程
的方程![]() 有解,则实数
有解,则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.如果方程![]() 的两个实根一个小于‒1,另一个大于1,那么实数
的两个实根一个小于‒1,另一个大于1,那么实数
m的取值范围是 ( )
A.![]() B.(-2,0) C.(-2,1) D.(0,1)
B.(-2,0) C.(-2,1) D.(0,1)
6.在![]()
![]() 三个结论:①
三个结论:①![]() ,②
,②![]()
③![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A.0 B.
7.若角α,β满足-![]() <α<β<
<α<β<![]() ,则2α-β的取值范围是 ( )
,则2α-β的取值范围是 ( )
A.(-π,0) B.(-π,π) C.(-![]() ,
,![]() ) D.(-
) D.(-![]() ,
,![]() )
)
8.设![]() 且
且![]() ,则 ( )
,则 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.目标函数![]() ,变量
,变量![]() 满足
满足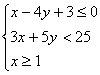 ,则有 ( )
,则有 ( )
A.![]() B.
B.![]()
![]() 无最小值
无最小值
C.![]() 无最大值
D.
无最大值
D.![]() 既无最大值,也无最小值
既无最大值,也无最小值
10.设M=![]() ,且a+b+c=1,(a、b、c∈R+),则M的取值范围是 ( )
,且a+b+c=1,(a、b、c∈R+),则M的取值范围是 ( )
A.[0,![]() ]
B.[
]
B.[![]() ,1] C.[1,8] D.[8,+∞)
,1] C.[1,8] D.[8,+∞)
第Ⅱ卷(非选择题,共100分)
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.设0<x≤3,1<y≤2005,是x-y的最大值与最小值的和是 .
 12.设
12.设![]() .
.
13.若方程![]() 有一个正根和一个负根,则实数
有一个正根和一个负根,则实数
![]() 的取值范围是__________________.
的取值范围是__________________.
14.f(x)的图象是如图两条线段,它的定义域是![]() ,则不等
,则不等
式![]() 的解集是 .
的解集是 .
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)(1)设a,b,x,y∈R,且a2+b2=1,x2+y2=1,求证:ax+by≤1;
(2已知a、b是不等正数,且a3-b3= a2-b2 求证:1< a +b<![]() .
.
16.(12分)解关于x的不等式ax2-(a+1)x+1<0.
17.(12分)(1)求![]() 的最小值;
的最小值;
(2)若![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
18.(12分)若f(x)是定义在(0,+∞)上的增函数,且对一切x>0满足![]()
(1)求![]() 的值; (2)若
的值; (2)若![]() ,解不等式
,解不等式![]()
19.(14分)要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种规格小钢板的块数如下表所示:
| 类 型 | A规格 | B规格 | C规格 |
| 第一种钢板 | 1 | 2 | 1 |
| 第二种钢板 | 1 | 1 | 3 |
|
20.(14分)(1)设不等式2x-1>m(x2-1)对满足m≤2的一切实数m的取值都成立,求x的取值范围;
(2)是否存在m使得不等式2x-1>m(x2-1)对满足x≤2的一切实数x的取值都成立.
参考答案(一)
一、ABDDD DCACD
二、11.2008;12.![]() ;13.
;13.![]() ;14.
;14.![]() 。
。
三、15.(1)证明:∵a2+x2≥2ax,b2+y2≥2by,
∴a2+x2+b2+y2≥2(ax+by),∴ax+by≤![]() =1。
=1。
又∵a2+x2≥-2ax,b2+y2≥-2by,
∴a2+x2+b2+y2≥-2(ax+by),∴ax+by≥-![]() =-1。
=-1。
∴ax+by≤1。
(2)证明:![]()
![]()
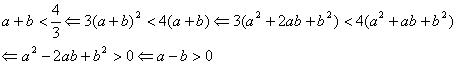
16.解:当a=0时,不等式的解为x>1;当a≠0时,分解因式a(x-![]() )(x-1)<0
)(x-1)<0
当a<0时,原不等式等价于(x-![]() )(x-1)>0,不等式的解为x>1或x<
)(x-1)>0,不等式的解为x>1或x<![]() ;
;
当0<a<1时,1<![]() ,不等式的解为1<x<
,不等式的解为1<x<![]() ;
;
|
当a=1时,不等式的解为 。
|
令![]() ,则
,则![]()
令![]() ,
,![]()
显然![]() 只有一个大于或等于2的根,
只有一个大于或等于2的根,
![]()
即![]() ,即
,即![]() 的最小值是
的最小值是![]() 。
。
解法二:![]()
令![]()
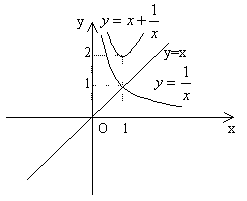
利用图象迭加,可得其图象(如下图)
![]()
当![]() 时,
时,![]() 递增,
递增,![]() 。
。
|

当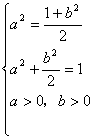
![]() 时,
时,![]() 的最大值为
的最大值为![]()
18.解: ![]() 则
则![]()
![]()
即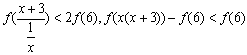
∴![]()
又![]() 在
在![]() 是增函数,则
是增函数,则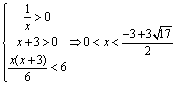 .
.
19.解:设需截第一种钢板![]() 张,第二种钢板
张,第二种钢板![]() 张,所用钢板面积为
张,所用钢板面积为![]() ,
,
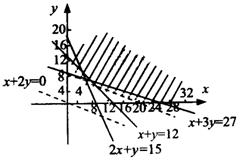 则有
则有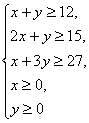
作出可行域(如图)
目标函数为![]()
作出一组平行直线![]() (t为参数).由
(t为参数).由![]() 得
得![]() 由于点
由于点![]() 不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使
不是可行域内的整数点,而在可行域内的整数点中,点(4,8)和点(6,7)使![]() 最小,且
最小,且![]() .
.
答:应截第一种钢板4张,第二种钢板8张,或第一种钢板6张,第二种钢板7张,得所需三种规格的钢板,且使所用的钢板的面积最小.
|
实数都有2x-1>m(x2-1)成立。
所以,![]() ,即
,即![]() ,即
,即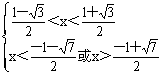
所以,![]() 。
。
(2) 令f(x)= 2x-1-m(x2-1)= -mx2+2x+(m-1),使x≤2的一切实数都有2x-1>m(x2-1)成立。
当![]() 时,f(x)= 2x-1在
时,f(x)= 2x-1在![]() 时,f(x)
时,f(x)![]() 。(不满足题意)
。(不满足题意)
当![]() 时,f(x)只需满足下式:
时,f(x)只需满足下式:
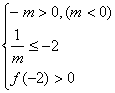 或
或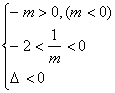 或
或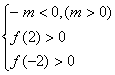
解之得结果为空集。
故没有m满足题意。