高中学生学科素质训练
新课标高二数学同步测试(2)(必修5第三章)
说明:本试卷分第一卷和第二卷两部分,第一卷50分,第二卷100分,共150分;答题时间120分钟。
第Ⅰ卷(选择题共50分)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.若![]() ,且
,且![]() ,则下列不等式一定成立的是 ( )
,则下列不等式一定成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.若![]() ,则下列不等关系中,不能成立的是 ( )
,则下列不等关系中,不能成立的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知实数x,y满足x2+y2=1,则(1-xy)(1+xy)有 ( )
A.最小值![]() 和最大值1 B.最小值
和最大值1 B.最小值![]() 和最大值1
和最大值1
C.最小值![]() 和最大值
和最大值![]() D.最小值1
D.最小值1
5.设x > 0, y > 0,![]() ,
, ![]() , a 与b的大小关系 ( )
, a 与b的大小关系 ( )
A.a >b B.a <b C.a ![]() b D.a
b D.a ![]() b
b
6.若关于![]() 的不等式
的不等式![]() 内有解,则实数
内有解,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() 时总有
时总有![]() 则实数
则实数![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.甲乙两人同时同地沿同一路线走到同一地点,甲有一半时间以速度m行走,另一半时间
以速度n行走;有一半路程乙以速度m行走,另一半路程以速度n行走,如果m ¹ n,甲
乙两人谁先到达指定地点 ( )
A.甲 B.乙 C.甲乙同时到达 D.无法判断
9.设![]() 满足约束条件组
满足约束条件组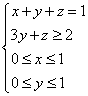 ,求
,求![]() 的最大值和最小值( )
的最大值和最小值( )
A.8,3 B.4,
10.设f(x)是奇函数,对任意的实数x、y,有![]()
则f(x)在区间[a,b]上 ( )
A.有最大值f (a) B.有最小值f (a)
C.有最大值![]() D.有最小值
D.有最小值![]()
第Ⅱ卷(非选择题,共100分)
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.已知![]() ,求
,求![]() 的取值范围
.
的取值范围
.
12.已知![]() .
.
13.函数![]() 的值域为
.
的值域为
.
14.要挖一个面积为
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)已知a, b都是正数,并且a ¹ b,求证:a5 + b5 > a2b3 + a3b2
16.(12分)设a>0, b>0,且a + b = 1,求证:![]() .
.
17.(12分)设![]() 且
且![]() ,求
,求![]() 的最大值.
的最大值.
18.(12分)已知![]() 的三边长
的三边长![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
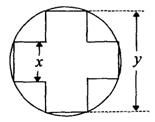 19.(14分)一变压器的铁芯截面为正十字型,为保证所需的磁通量,要求十字应具有
19.(14分)一变压器的铁芯截面为正十字型,为保证所需的磁通量,要求十字应具有![]() 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽![]() 及长
及长![]() ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
|
若![]() ,求实数a的取值范围.
,求实数a的取值范围.
参考答案(二)
一、DBABB ADACB
二、11.![]() ; 12.8; 13.
; 12.8; 13.![]() ; 14.长
; 14.长
三、15.证:(a5 + b5 ) - (a2b3 + a3b2)
= ( a
= a3 (a2 - b2 ) - b3 (a2 - b2) = (a2 - b2 ) (a3 - b3)
= (a + b)(a - b)2(a2 + ab + b2)
∵a, b都是正数,∴a + b, a2 + ab + b2 > 0
又∵a ¹ b,∴(a - b)2 > 0 ∴(a + b)(a - b)2(a2 + ab + b2) > 0
即:a5 + b5 > a2b3 + a3b2
16.证:∵![]() ∴
∴![]() ∴
∴![]()
∴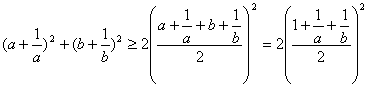
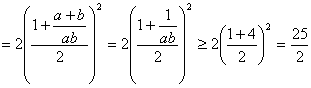
17.解:∵![]() ∴
∴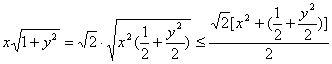
又![]() ∴
∴![]()
即![]()
18.解:解:设![]() ,
,![]() ,则
,则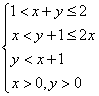 ,
,
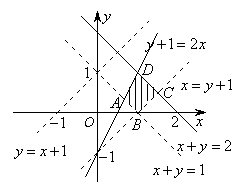 作出平面区域(如右图),
作出平面区域(如右图),
由图知:![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.
19.解:设![]() 由条件知:
由条件知:
![]() 即
即![]()
设外接圆的半径为R,即求R的最小值,
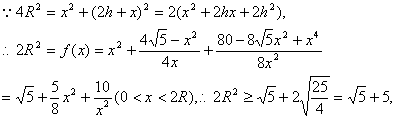
等号成立时,![]()
∴当![]() 时R2最小,即R最小,从而周长
时R2最小,即R最小,从而周长![]() 最小,
最小,
|
20.解![]() 的意义是方程
的意义是方程![]() 有解,
有解,
且至少有一解在区间![]() 内,但直接求解情况比较多,如果考虑“补集”,
内,但直接求解情况比较多,如果考虑“补集”,
则解法较简单.
设全集![]()
且![]() 的两根都在[1,4]内}
的两根都在[1,4]内}
记![]() ∴方程
∴方程![]() 的两根都在[1,4]内
的两根都在[1,4]内
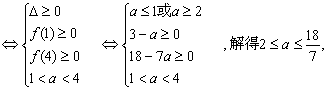
![]() ,∴所求实数a的取值范围是
,∴所求实数a的取值范围是![]()
