宿迁市2004－2005学年度第二学期期末试卷高二数学
本试卷分第I卷（选择题）和第II卷（非选择题）两部分
总分：150分 考试时间：120分钟
第I卷（选择题：共60分）
一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1、函数f(x)=2的导数是 （ ）
A. 2
B.
2、在棱长为1的正方体ABCD-A1B
A. 
B.
C. 1 D. 
.
3、高二年级12个班共有580人，要采用分层抽样的方法从高二年级的全体学生中抽取一个容量为60的样本，已知某班有58名学生，那么从该班抽取的学生数是 （ ）
A. 5 B.
4、已知直线l，m，n及平面α，下列命题中的假命题是 （ ）
A.若l∥m，m∥n，则l∥n B.若l⊥α，m∥α，则l⊥m
C.若l⊥m，m∥n，则l⊥n D.若l∥α，n∥α，则l∥n.
5、已知球面上两点的球面距离为
，则球的半径为
( )
A. 
cm B. 
cm C. πcm D. 3πcm .
6、已知函数f(x)=
x3+
x2+tx是R上的单调增函数，则t的值可能是 （ ）
A. t=1 B. t=
7、一个半径为R的球与体对角线长为l的正方体的六个面都相切，则R与l的关系是 （ ）
A. l=
R B. l=2R C. l=2R D. 2R=l.
8、函数y=f(x)在 [a ,b]上 （ ）
A.极大值一定比极小值大 B.极大值一定是最大值
C.最大值一定是极大值 D.最大值一定大于极小值.
9、5名工人分别要在3天中选择1天休息，不同方法的种数有 （ ）
A. 53 B. 
D. 
.
10、正三棱锥侧面均为直角三角形，其体积为
，则底面边长是 （ ）
A. 1 B.
11、4名学生参加数、理、化竞赛，每门学科至少有1人参加，则不同的参赛方案有（ ）
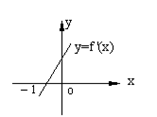A. 12种 B. 24种
C. 36种 D. 48种.
12、已知函数y=f(x)的导函数y=f ' (x)的图象
如图所示，则y=f(x)的图象可能是下图中的 （ ）
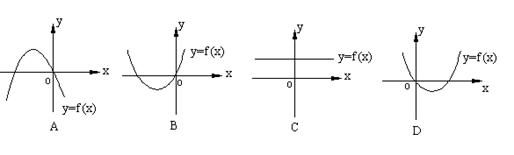
二、填空题(本大题共4小题，每小题4分，共16分，把答案填在题中的横线上)
13、已知曲线y =x3+
，则过点P（2，4）的切线方程是 .
14、空间有3个平面，其中没有两个互相平行，则一共有________条交线.
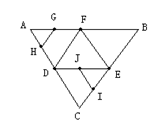
15、如图，在正三角形ABC中，D、E、F分别为各边的中点，G、H、I、J分别为AF、AD、BE、DE的中点，则将ΔABC沿DE、EF、FD折成三棱锥后，GH与IJ所在直线所成的角的大小为 .
16、杨辉是我国南宋著名的数学家，“杨辉三角”是杨辉的一大重要研究成果，其中蕴含了许多优美的规律（如图）， “杨辉三角”中第14行从左到右第10与第11个数的比值为__________.
第1行 1 1
第2行 1 2 1
第3行 1 3 3 1
第4行 1 4 6 4 1
第5行 1 5 10 10 5 1
宿迁市高二年级2004－2005学年度第二学期期末试卷
第Ⅱ卷（选择题：共60分）
一、选择题：（共12题，每题5分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：（共4题，每题4分）
13 ； 14 ； 15 ；16 .
三、解答题（本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤）
17、（本小题满分12分）
将5盆名花排成一列展览，
（Ⅰ）牡丹花恰好放在正中间的概率；
（Ⅱ）牡丹花、玫瑰花恰放在两端的概率.
18、（本小题满分12分）
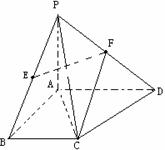如图，在四棱锥P-ABCD中，PA、AB、AD两两互相垂
直，BC∥AD，且AB=AD=2BC，E，F分别是PB、PD
的中点。
（Ⅰ）证明：EF∥平面ABCD；
（Ⅱ）若PA=AB，求PC与平面PAD所成的角.
19、（本小题满分12分）
（Ⅰ）求(x2+1)(x-2)5展开式中含x6项的系数。
（Ⅱ）若(x2+1)(x-2)5 = a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7,
求a0+a1+a2+…+a7.
20、（本小题满分12分）
甲、乙、丙三人各进行一次投篮，如果3人投中的概率都是0.4，
计算：（Ⅰ）3人都投中的概率；
（Ⅱ）至多1人投中的概率。
21、（本小题满分12分）
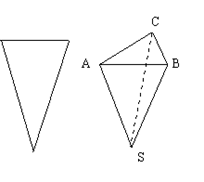
用三个全等的等腰三角形拼接成一个正三棱锥形的漏斗（如图）。
已知三角形的一腰长为2.
(Ⅰ)将漏斗容积V表示成关于三棱锥高h的函数关系式.
(Ⅱ)求漏斗容积的最大值，并求此时漏斗的高与等腰三角形的顶角大小.
22、（本小题满分14分）
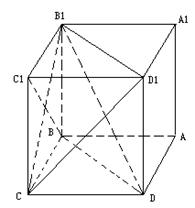
如图，在棱长为1的正方体ABCD-A1B
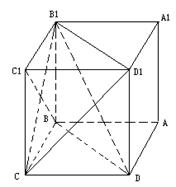（Ⅰ）求证：BC1⊥平面CDB1；
（Ⅱ）求二面角B-B1D-C的大小；
（Ⅲ）求三棱锥D1-CDB1的体积。
宿迁市高二年级2004－2005学年度第二学期期末试卷
参考答案
一、选择题：（共12题，每题5分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | C | B | D | B | A | B | D | B | B | C | B |
二、填空题：（共4题，每题4分）
13 y = 4x-4 ；14 1个或3个 ；15 60° ；16 2 .
三、解答题：
17、解：（Ⅰ）记：“5盆花排成一列,牡丹花在正中间”为事件A---------------------1分
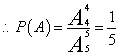--------------------------------------------------------------5分
答：牡丹花在正中间概率为
-----------------------------------------------
6分
（Ⅱ）记：“5盆花排成一列,牡丹花、玫瑰花恰好在两端”为事件B-------7分
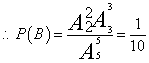--------------------------------11分
答：牡丹花、玫瑰花恰好在两端概率为
-------------------------------12分
18、（Ⅰ）证明：连结BD
∵在ΔPBD中，E，F分别为PB、PD中点
∴EF∥BD----------------------------------------------------------2分
又EF
平面ABCD
∴EF∥平面ABCD----------------------------------------------4分
（Ⅱ）解：取AD中点G，连接CG、PG
∵四边行ABCD中，BC∥AD，AD=2BC
∴CG∥AB --------------------------------------------------------6分
又∵AB⊥AD，AB⊥AP，AP∩AD=A
∴AB⊥平面PAD
∴CG⊥平面PAD
∴∠GPC是PC与平面PAD所成的角-------------------9分
设PA=
a
∴PC=
=
在RTΔPGC中，sin∠GPC=
∴∠GPC= arcsin
即PC与平面PAD所成的角是arcsin----------------12分
19、解：（Ⅰ）∵(x2+1)(x-2)5展开式中含x6项的系数就是（x-2）5
展开式中含x4项的系数-------------------------------------------2分
∴所求的系数是
×（-2）=
-10-------------------------------5分
（Ⅱ）∵(x2+1)(x-2)5= a0+a1(x-1)+a2(x-1)2+…+a7(x-1)7
∴当x=1时，a0= -2-----------------------------------------------8分
∴当x=2时，a0+a1+a2+…+a7=0-------------------------------11分
∴a1+a2+…+a7= - a0=2--------------------------------------------12分
20、解：（Ⅰ）记“甲投篮一次，投中”为事件A，
“乙投篮一次，投中”为事件B，
“丙投篮一次，投中”为事件C ---------------------------1分
则A，B，C为相互独立事件 --------------------------------2分
∵“3人都进行一次投篮，都投中”发生，即事件A，B，C同时发生
∴P（A·B·C）= P（A）·P（B）·P（C）
=0.4×0.4×0.4
= 0.064------------------------------------------- ---4分
答：3人都投中概率是0.064-------------------------------------5分
（Ⅱ）“3人都各进行一次投篮，至多1人都投中”可分为两类：
第一类是无一人投中，概率是P（
·
·
）=P（）·P（）·P（）
=（1-0.4）·（1-0.4）·（1-0.4）
=0.216------------------------7分
第二类是有且只有一人投中，又分三种情况：
第一种是甲投中，乙、丙未投中，
P（A··）= P（A）·P（）·P（）
= 0.4·（1-0.4）·（1-0.4）
= 0.144
第二种是乙投中，甲、丙未投中，同理P（·B·）=0.144
第二种是丙投中，甲、乙未投中，同理P（··C）=0.144------9分
∴P（··）+P（A··）+P（·B·）+P（··C）
= 0.648--------------------------------------------------------------------11分
答：至多1人都投中的概率是0.648-------------------------------------------12分
21、解：（Ⅰ）设等腰三角形的底边长为a,则三棱锥底面三角形边上的高为
∴(
)2+h2=4 即h2+
a2 = 4 ------------------ ------ -----------3分
∴V=×
×a2×h=
=
---- 6分
（Ⅱ）∵V'=
令V'=0 即h=
------------------------------------8分
当0<h<时，V'>0
当<h<2时,V'<0
∴h=时V取得极大值为
并且这个极大值是最大值（11分）
把h=代入h2+a2=4得a=2
∴在△ASB中，∠ASB=
即漏斗容器的最大值为，此时漏斗的高为，等腰三角形的顶角为.-----14分
22、（Ⅰ）证明：在正方体ABCD-A1B
且四边形BCB
∴CD⊥BC1，B
∴BC1⊥平面CDB1---------------------------------4分
（Ⅱ）解：设B
由BC1⊥平面CDB1知：BE⊥B1D
∴∠BEO为二面角B-DB1-C的平面角 ------- 6分
在正方形BC C1B1中，BC=CD= 1，
∴B1O=BO=OC= ，
∵Rt△DCB1∽Rt△OCB1
∴OE=
--------------8分
∴tan∠BEO=
即∠BED=60°
∴二面角B-AB1-C为60°--------------------------10分
（Ⅲ）解：∵B
∴
-------14分