高二下数学第一次月考试卷（文科）
（考试范围：统计案例、推理和证明）
班级：_________ 姓名：__________ 学号__________ 成绩：
| 题 号 | 一 | 二 | 三 | 总 分 | |||||
| 17 | 18 | 19 | 20 | 21 | 22 | ||||
| 分 数 | |||||||||
说明：本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。试卷满分150，考试时间120分钟。
积化和差公式：sina cosb=
[sin(a+b)+sin(a-b)];cosa sinb=[sin(a+b)-sin(a-b)];
cosa cosb=[cos(a+b)+cos(a-b)]; sina sinb=-[cos(a+b)-cos(a-b)].
第 Ⅰ 卷(选择题 共60分)
| 得分 | 评卷人 |
一、选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，有一项是符合题目要求的，请将所选答案填在指定的答题栏内。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1 .儿子的身高和父亲的身高是： ( )
(A)确定性关系 (B) 相关关系 (C)函数关系 (D)无任何关系
2. 用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（ ）。
(A)假设三内角都不大于60度； (B) 假设三内角都大于60度；
(C) 假设三内角至多有一个大于60度； (D) 假设三内角至多有两个大于60度。
3.设两个变量x和y之间具有线性相关关系，它们的相关系数是r，y关于x的回归直线的斜率是b，纵截距是a，那么必有（）
（A) a与r的符号相反 (B) a与r的符号相同 (C) b与r的相反 (D) b与r的符号相同
4. 在三维柱形图中，主对角线上两个柱形高度的乘积与副对角线上的两个柱形的高度的乘积相差越大两个变量有关系的可能性就（ ）
(A) 越大 (B) 越小 (C)无法判断 (D) 以上都不对
5. 由①正方形的对角线相等；②平行四边形的对角线相等；③正方形是平行四边形，根据“三段论”推理出一个结论，则这个结论是 （ ）
(A) 正方形的对角线相等 (B) 平行四边形的对角线相等
(C) 正方形是平行四边形 (D)其它
6. 在吸烟与患肺病这两个分类变量的计算中，下列说法正确的是（ ）
(A) 若K2的观测值为k=6.635,我们有99%的把握认为吸烟与患肺病有关系，那么在100个吸烟的人中必有99人患有肺病;
(B) 从独立性检验可知有99%的把握认为吸烟与患肺病有关系时，我们说某人吸烟，那么他有99%的可能患有肺病;
(C)若从统计量中求出有95% 的把握认为吸烟与患肺病有关系，是指有5% 的可能性使得推判出现错误;
(D)以上三种说法都不正确。
7. 一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是 ( )
(A)12 (B) 13 (C)14 (D)15
8. 已知x与y之间的一组数据：
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
则y与x的线性回归方程为y=
x+
必过点（ ）
(A)（2，2） (B)（1.5，0） (C)（1，2） (D)（1.5，4）
9. 观察下列数:1,3,2,6,5,15,14,x,y,z,122,…中x,y,z的值依次是 ( )
(A)42,41,123; (B) 13,39,123; (C)24,23,123; (D)28,27,123.
10. 考察棉花种子经过处理跟生病之间的关系得到如下表数据：
| 种子处理 | 种子未处理 | 合计 | |
| 得病 | 32 | 101 | 133 |
| 不得病 | 61 | 213 | 274 |
| 合计 | 93 | 314 | 407 |
根据以上数据，则( )
(A)种子经过处理跟是否生病有关; (B)种子经过处理跟是否生病无关;
(C)种子是否经过处理决定是否生病; (D)以上都是错误的.
11. 在下列表格中,每格填上一个数字后,使每一行成等差数列,每一列成等比数列,则a+b+c的值是( )
| 1 | 2 | |||
| 0.5 | 1 | |||
| a | ||||
| b | ||||
| c |
(A) 1 (B) 2 (C) 3 (D) 4
12. 下列四个命题：①若0<a<
,则cos(1+a)<cos(1-a);②若0<a<1,则
>1+a>
;③若x、y
R，满足y=x
,则log
的最小值是
；④若a、bR，则
。其中正确的是（ ）。
(A) ①②③ (B) ①②④ (C)②③④ (D)①②③④
第Ⅱ卷 (非选择题 共90分)
| 得分 | 评卷人 |
二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中的横线上．
13. 由数列的前四项: 
,1 , 
,
,……归纳出通项公式a n =___ _.
14. 在研究身高和体重的关系时，求得相关指数
______________，可以叙述为“身高解释了64%的体重变化，而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
15. 在求两个变量x和y的线性回归方程过程中,计算得
=25, 
=250, 
=145, 
=1380,则该回归方程是
.
16.对于平面几何中的命题“如果两个角的两边分别对应垂直,那么这两个角相等或互补”,在立体几何中,类比上述命题,可以得到命题: “ ”,这个类比命题的真假性是 .
三、解答题：本大题共6小题，满分74分.解答应写出文字说明、证明过程或演算步骤。
17. （14分）求证：(1)
;(2) 
+
>2
+
。
18.（12分）如图，S为△ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC。
求证：AB⊥BC.
19. （12分）求证：
是无理数。
20.（12分）某种书每册的成本费y（元）与印刷册数x（千册）有关，经统计得到数据如下：
| x | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | 100 | 200 |
| y | 10.15 | 5.52 | 4.08 | 2.85 | 2.11 | 1.62 | 1.41 | 1.30 | 1.21 | 1.15 |
检验每册书的成本费y与印刷册数的倒数
之间是否具有线性相关关系，如有，求出y对x的回归方程。(计算结果精确到0.001)
21.（12分）观察以下各等式：
，分析上述各式的共同特点，猜想出反映一般规律的等式，并对等式的正确性作出证明。
22. （12分）从社会效益和经济效益出发，某地投入资金进行生态环境建设，并以此发展旅游产业。根据规划，本年度投入800万元，以后每年投入将比上年减少
。本年度当地旅游业收入估计为400万元，由于该项建设对旅游业的促进作用，预计今后的旅游业收入每年会比上年增加
。
（1）设n年内（本年度为第一年）总投入为an万元，旅游业总收入为bn万元，写出an, bn的表达式；
（2）至少经过几年旅游业的总收入才能超过总投入？
参考答案
一、 选择题
1．B 2.B 3.D 4.A 5.A 6.C
7.C 8.D 9.A 10.B 11.A 12.B
一. 填空(4′×4)
13. 
14. 0.64
15. 
=6.5x+17.5。
16.如果两个二面角的两个半平面分别对应垂直，则这两个二面角相等或互补。假命题。（答案不唯一）
三.解答与证明
17.（1） ∵
,
,
;将此三式相加得
2
,∴. （7分）
（2）要证原不等式成立，只需证（+）
>（2+），即证
。
∵上式显然成立, ∴原不等式成立. （14分）
18.证明：如图，作AE⊥SB于E.
∵平面SAB⊥平面SBC，∴AE⊥平面SBC，（4分）
∴AE⊥BC.
（6分）
又∵SA⊥平面ABC，∴SA⊥BC， （8分）
∵SA
AE=A，SA
平面SAB，AE平面SAB，
∴BC⊥平面SAB， （10分）
∴AB⊥BC. （12分）
19. 假设是有理数， （2分）
则存在互质的整数m,n使得
， （4分）
∴m=n , ∴
=2n, ∴ 是偶数，从而m也是偶数；（7分）
∴设m=2k(k
),则4
=2n，即n=2，∴n也是偶数，从而n也是偶数；（10分）
这与m,n互质矛盾！所以假设不成立，∴是有理数。 （12分）
20、解：首先设变量
，题目所给的数据变成如下表所示的数据
|
| 1 | 0．5 | 0．333 | 0．2 | 0．1 | 0．05 | 0．033 | 0．02 | 0．01 | 0．005 |
|
| 10.15 | 5.52 | 4.08 | 2.85 | 2.11 | 1.62 | 1.41 | 1.30 | 1.21 | 1.15 |
（4分）
经计算得
,从而认为
与y之间具有线性相关关系，
(6分）
由公式得
（9分）
所以
（10分）
最后回代，可得
（12分）
21．（12分）猜想：
。 （6分）
证明：
（12分）
22、 解：（1）第1年投入为800万元，第2个投入为
万元，……，第n年投入为
万元。
（3分）
∴n年内的总投入为
=
=
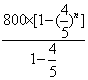. （5分）
第1年旅游业收入为400万元，第2年旅游业收入为
万元，……，第n年旅游业收入为 
万万元。
（6分）
∴n年内的旅游业总收入为
=
=
(8分)
（2）设至少经过n年旅游业的总收入才能超过总投入，由此bn-an>0,即
,
设
,代入上式得5x2-7x+2>0,解此不等式，得
或x>1 (舍去)。
即
，由此得n>5。
（11分）
答：至少经过6年旅游业的总收入才能超过总投入。 （12分）