仪征电大附属中学2005—2006年度第一学期高二
年级第一次月考数学试卷
命题人：陈宏强
一、选择题（本大题共12小题，每小题5分，共60分）
1．若直线
的倾斜角为
，则
（ ）
A．等于0 B．等于
C．等于
D．不存在
2．与直线
关于点
对称的直线方程是（ ）
A．
B．
C．
D．
3．两条直线
与
的夹角的正弦值是（ ）
A．
B．
C．
D．
4．直线
被曲线
所截得的线段的中点坐标是( )
A．
B．（0，0） C．
D．
5．点P(2,3)到直线：ax+(a－1)y+3=0的距离d为最大时，d与a的值依次为 （ ）
A．3,-3 B．5,1 C．5,2 D．7,1
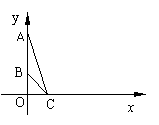6．如图，设点C(1,0)，长为2的线段AB在y轴上滑动，则直线AB、AC所成的最大夹角
是 （ ）
A．30° B．45°
C．60° D．90°
7．已知x,y满足约束条件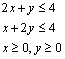 
，则
的最大值是 （ ）
A．
B．
C．2
D．4
8．F1，F2是定点，且F1F2=6，动点M满足MF1+MF2=6，则M点的轨迹方程是( )
A．椭圆 B．直线 C．圆 D．线段
9．圆
上的点到直线
的距离的最大值是--------------( )
A．
B．
C．
D．0
10．已知方程
表示焦点在
轴上的椭圆，则
的取值范围是( )
A．m<1 B．-1<m<1 C．m>1 D．0<m<1
11．当
时，方程
所表示的图形----------------( )
A．关于
轴对称
B．关于轴对称
C．关于直线
对称
D．关于直线
对称
12．曲线
所表示的图形是---------------------( )
 |  |  |  | ||||
A． B． C． D．
二、填空题（本大题共6小题，每小题4分，共24分）
13．点
到直线
的距离等于4，且在不等式
表示的平面区域内，则点
的坐标是_______________.
14．若实数x,y满足
的最大值是
．
15. 圆
截直线
所得的弦长是
。
16．直线y
= x + b与曲线x=
有且仅有一个公共点，则b的取值范围是
.
17．已知定点
，
，点M与A、B两点所在直线的斜率之积等于
，则点M的轨迹方程是
18．椭圆的两焦点为
，
，过F1作弦AB，且
的周长为20，则此椭圆的方程为
三、解答题（本大题共6小题，共66分）
19．（10分）已知直线
满足下列两个条件：
（1）过直线y = – x + 1和y = 2x + 4的交点;
（2）与直线x –3y + 2 = 0 垂直，
求直线的方程．
20．（10分）求经过点
，和直线
相切，且圆心在直线
上的圆方程．
21．（10分）P为椭圆
+
=1上一点，F1，F2为焦点，∠F1PF2=30°，求ΔPF1F2的面积。
22．（12分）已知曲线
与直线
交于A、B两点，O为原点，若OA┴OB,求m的值．
23．（12分）某承包户承包了两块鱼塘，一块准备放养鲫鱼，另一块准备放养鲤鱼，现知放养这两种鱼苗时都需要鱼料A、B、C，每千克鱼苗所需饲料量如下表：
| 鱼类 | 鱼料A | 鱼料B | 鱼料C |
| 鲫鱼/kg | 15g | 5g | 8g |
| 鲤鱼/kg | 8g | 5g | 18g |
如果这两种鱼长到成鱼时，鲫鱼和鲤鱼分别是当时放养鱼苗重量的30倍与50倍，目前这位承包户只有饲料A、B、C分别为 120g、50g、144g,问如何放养这两种鱼苗，才能使得成鱼的重量最重．
24．（12分）已知与曲线C：
相切的直线交
的正半轴与
两点，O为原点，
=a，
，
．
（1）求线段
中点的轨迹方程；
（2）求
的最小值．
答案：
1.C,2.A,3.C,4.A,5.B,6.D,7.B,8.D,9.C,10.D,11.D,12.B
13．（
，3）
14．
15．2
16．
或
17．
18．
19．由
得交点 ( –1, 2 )， ∵ k l =
– 3, ∴
所求直线的方程为: 3x + y + 1 = 0.
20．所求圆的方程为：
．
21．
，
22．
23．设放养鲫鱼xkg,鲤鱼ykg,则成鱼重量为
,其限制条件为 
，画出其表示的区域（如图），不难找出使30x+50y最大值为428kg.
答：鲫鱼放养3.6kg,鲤鱼放养6.4kg,此时成鱼的重量最重．
24．（1）设AB的中点为P(x,y) ,圆C的方程化简为：
又直线的方程为：
，
，
①，又∵P是AB的中点，
，代入①得
，即线段中点的轨迹方程为；
．
（2）
，
，
.∴
．