仪征电大附属中学2005—2006年度第一学期
高二期末统测模拟试题
姓名：___________ 班级：__________ 得分：___________
一、选择题(5*12=60分)
1．平面内有两定点A、B及动点P，设命题甲是：“PA+PB是定值”，命题乙是：“点P的轨迹是以A．B为焦点的椭圆”，那么 （ ）
A．甲是乙成立的充分不必要条件 B．甲是乙成立的必要不充分条件
C．甲是乙成立的充要条件 D．甲是乙成立的非充分非必要条件
2. 直线
的倾斜角为
，且
，则
、
满足
A．
B．
C．
D．
3. 在空间，下列命题正确的是 （ ）
（A）二组对边分别相等的四边形是平行四边形
（B）四边相等的四边形是平行四边形
（C）有一组对边相等且平行的四边形是平行四边形
（D）两组对角分别相等的四边形是平行四边形
4. 圆
与直线
（
且
）的位置关系是
A．相交 B．相切 C．相离 D．不确定
5. 方程x+
=0所表示的图形是 （
）
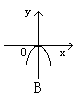
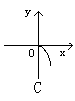
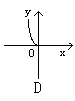
6．直线
与椭圆
恒有公共点，则b的取值范围是（ ）
A．（0，1） B．（0，5） C．
D．
7.
若关于
的不等式
有解，则实数的取值范围是（ ）
A．
B．
C．
D．
8. 过点(2,-2)且与双曲线x2-2y2=2有公共渐近线的双曲线方程是（ ）
A、
B、
C、
D、
9. 已知
，则
的取值范围是
A．
B．
C．
D．
10. 原点O到直线
的距离设为
，当正数
变动时，的最大值为
A．
B．
C．1
D．2
11、已知P是椭圆
上一点，F1、F2是椭圆的两个焦点，若∠P F1F2=600，∠P F2 F1=300，则该椭圆的离心率为（ ）
A 
B
C
D
12．曲线f（x，y）＝0关于直线x－y－2＝0对称的曲线方程是 ( )
A．f（y＋2，x）＝0 B．f（x－2，y）＝0
C．f（y＋2，x－2）＝0 D．f（y－2，x＋2）＝0
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
二、填空题（4*4=16分）
13、双曲线
与椭圆
有共同的焦点，则m=
．
14、一动圆M和直线l：x= —2相切，且经过点F（2，0），则圆心的轨迹方程是 .
15. 约束条件
所表示的区域中，整点共有___个
16．点
在椭圆
上则
的最小值为____________。
三、解答题（17，18,19,20,21题12分、、22题14分）
17、已知直线
过点
，分别求满足下列条件的的方程：
（1）与坐标轴在第一象限所围成之三角形面积最小；
（2）在轴、
轴正半轴上的交点分别为A、B，MA·MB最小。
18. 已知一个圆截y轴所得的弦为2，被x轴分成的两段弧长的比为3∶１．（1）设圆心为（a，b），求实数a，b满足的关系式；（2）当圆心到直线l：x－2y＝0的距离最小时，求圆的方程．
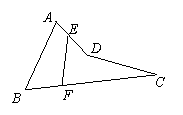19．如图，空间四边形ABCD的两对边AB＝CD＝3，E，F
分别是另两对边AD，BC上的点，且AE∶ED＝BF∶FC
＝1︰2，EF＝，求对边AB与CD所成角的大小．
20．某家俱公司生产甲、乙两种型号的组合柜，每种柜的制造白坯时间、油漆时间及有关数据如下：
| 工艺要求 | 产品甲 | 产品乙 | 生产能力/（台） |
| 制白坯时间/天 | 6 | 12 | 120 |
| 油漆时间/天 | 8 | 4 | 64 |
| 单位利润/元 | 20 | 24 |
问该公司如何安排甲、乙二种柜的日产量可获最大利润，并且最大利润是多少？
21．已知双曲线
（1）过右焦点F2作一条渐近线的垂线（垂中为A），交另一渐近线于B点，求证：线段AB被双曲线的左准线平分；
（2）过中心O作直线分别交双曲线左、右支于C、D两点，且
的面积为20，求直线CD的方程。
22、已知抛物线y2=2px(p>0)与圆(x-2)2+y2=3相交，A、B是它们在x轴上方的交点（如图）若线段AB的中点M在直线y=x上，求p的值。
 |
答案：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| A | D | C | C | D | C | D | A | D | A | A | C |
13.
；
14.
;
15.8;
16. —1.
17.(1).
(2).
18.(1).
(2)
或
19.
20. 甲4台、乙8台获最大利润，最大利润272元。
21.(1)
(2)
22.