泰州市2005～2006学年度第一学期期末调研考试

高二数学试题

 (考试时间120分钟　 总分150分)

注意事项：

1、本试卷共分两部分，第Ⅰ卷为选择题，第Ⅱ卷为非选择题。

2、所有试题的答案均填写在答题纸上（选择题部分使用答题卡的学校请将选择题的答案直接填涂到答题卡上），答案写在试卷上的无效。

第I卷选择题（共60分）

一、选择题(本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目的要求。)

1、过点且与直线垂直的直线方程是

　 A.　　　 B.　 　 C.　　 D.

2、若α,β是空间的两个不同平面，则它们公共点的个数是

　 A.只能是0个　　　　 B.0或1个　　　　 　C.无数个　　　　　　D.0或无数个

3、圆关于原点（0，0）对称的圆的方程为　　

A.　　　　　　　　　 B.

C.　　　　　　  D.

4、以椭圆的焦点为顶点，顶点为焦点的双曲线方程是

　 A.　　　 B.　　　C.　　　D.

5、若双曲线的一条准线方程为，则该双曲线的离心率为

A.　　　　　　　 B.　　　　　　　　C.　　　　　　　D.

6、若正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线y²=2px（p>0）上，则这个正三角形的面积是

A.　　　　B.　　  C.　　　 D.

7、已知、是两条不同的直线，α、β是两个不同的平面，给出下列四个命题

（1）若∥ ∥则∥　（2）若∥ ⊥则⊥

（3）若则　　 （4）若则

　 其中真命题的个数是

A.0个　　　　 　 B.1个　　　　　 C.2个　　　 D.3个

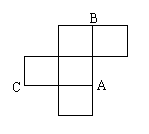
8、如图是一个无盖的正方体盒子展开后的平面图，A、B、C是展开图上的三点，则在正方体盒子中，∠ABC的值为

　 A.180°　　　　　B.120°　　　　 C.60° 　　 D.45°

9、设M为平面上以A（4，1），B（－1，－6），C（－3，2）为顶

点的三角形区域（包括边界），则z=4x－3y在M上的最大值

与最小值分别为

　　A.最大值为14，最小值为－18　　　B.最大值为－14，最小值为－18

C.最大值为18，最小值为14　　　 D.最大值为18，最小值为－14

10、设F₁、F₂是椭圆的两个焦点，点P在椭圆上，且△F₁PF₂的面积为1，

则 的值为

A.1　 　　　　　B.0　　　　  　 C.　　　　 D.2

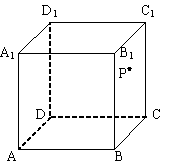
11、如图，在正方体中，P是侧面内

一动点，若P到直线BC与直线的距离相等，则动点　

P的轨迹所在的曲线是　　

　 A.直线　　　　　 B.圆　 　　　　　C.双曲线　 　D.抛物线

12、设，若，且，

则的取值范围是

　　A.　　　　 B.　　 　　　C. 　　D.

第Ⅱ卷

请在各题目的答题区域内作答，超出黑色矩形边框限定区域的答案无效

　非选择题(共90分)

二、填空题(本大题共6小题，每小题4分，共24分，把答案填在答题纸上。)

13、不等式的解集为　　 ▲　　  .

14、双曲线的渐近线方程为　　 ▲　　  .

15、在正方体ABCD—A₁B₁C₁D₁各表面上的对角线中，与体对角线AC₁垂直的面对角线共有

　　 ▲　　　条.

16、若抛物线的顶点在原点，对称轴为y轴，焦点在

直线x+2y+12=0上，则抛物线的方程为　　 ▲　　  .

17、如图，长方体ABCD—A₁B₁C₁D₁中，AA₁=AB=2，

AD=1，点E、F、G分别是DD₁、AB、CC₁的中点，

则异面直线A₁E与GF所成的角的大小

为　　 ▲　　　.

18、直线与圆没有公共点，若以为点的坐标，

则过点 的一条直线与椭圆的公共点有　　▲  　个.

三、解答题(本大题有5小题，共66分。解答应写出必要的文字说明、证明过程或演算步骤)

19、（本小题满分12分）

已知以为圆心的圆C与直线相切．

求(1)圆C的方程；

　　 (2)轴被圆C所截得的弦长．

20、（本小题满分12分）

如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，

E、F分别是棱AA₁、CC₁的中点．

(1)求点E到面对角线BD的距离；

(2)求证：四边形BED₁F是菱形．

21、（本小题满分14分）

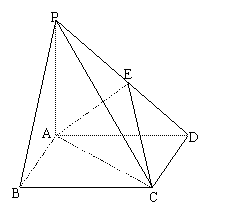
如图，已知点P是边长为1的正方形ABCD所在平面外一点，且PA⊥平面ABCD，点E为PD中点．

(1)求证：PB//平面EAC；

(2)求异面直线PB与AC所成的角的取值范围．

22、（本小题满分14分）

已知椭圆C的中心在原点，焦点在轴上，离心率是，且左顶点与右焦点F的距离为3.

(1)求椭圆C的方程；

(2)过点F的直线交椭圆C于A、B两点, A、B在右准线上的射影分别为M、N．

求证：AN与BM的交点在x轴上．

23、（本小题满分14分）

已知定点A(-2,0),B(2,0)，曲线E上任一点P满足.

　 (1)求曲线E的方程；

　 (2)延长PB与曲线E交于另一点Q，求PQ的最小值；

　 (3)若直线的方程为，延长PB与曲线E交于另一点Q，如果存在某一位

置，使得PQ的中点R在上的射影C满足PCQC，求的取值范围．

泰州市2005～2006学年度第一学期期末联考

高二数学参考答案

一、选择题(每小题5分，共60分)

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	D	A	C	D	B	B	C	A	B	D	A

二、填空题(本大题共6小题，每小题4分，共24分，把答案填在题目的横线上。)

13、　　  14、　　　　15、6

16、　　　　　　  17、　　　　　　 18、2

19、（本小题满分12分）

解：（1）因为圆心为C，所以可设圆C的方程为

由它与直线相切得，即

所以圆C的方程为　　 ……（6分）

  （2）圆心C到轴的距离是1，则轴被圆C所截得的弦长为　　　　　　　 　　　 

　　　 所以轴被圆C所截得的弦长为　　　　……（12分）

20、（本小题满分12分）

（1）解：连结AC与BD交于O点，连EO　　则　　　　 在平面ABCD上的射影为AO　　　

这样点E到面对角线BD的距离即为EO的长……（3分）

在中，，则

即点E到面对角线BD的距离为……（6分）

2）证明：取DD₁的中点M，连结AM，FM

　，四边形FMAB为平行四边形　　　 　　 

则BF//AM，且BF=AM

又四边形AMD₁E也是平行四边形，

则ED₁//AM，且ED₁=AM　　 BF//ED₁，且BF=ED₁

 所以四边形EBFD₁是平行四边形，（10分）

A

B

又EB==BF 　　这样四边形EBFD₁是菱形……（12分）

21、（本小题满分14分）

（1）证明：连结BD交AC于O点，连结EO

 因为点E为PD中点，点O为BD中点

所以EO//PB，又PB不在平面ACE上

EO在平面ACE内　 所以PB//平面ACE　 ……（6分）

（2）解：设PA=，则

在中，AE是其中线，AE=

在中，OE是其中位线，OE=

所以AEO为等腰三角形，且……（8分）

EO//PB，则即为异面直线PB与AC所成的角……（10分）

取OA的中点M，则EMAO，在中

（）

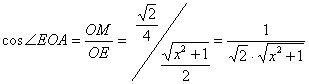所以异面直线PB与AC所成的角的取值范围是……（12分）

22、（本小题满分14分）

（1）解：设椭圆C的方程为（）

则由，得

所以椭圆C的方程为……（6分）

（2）证明：①当AB垂直于轴时, AB的坐标分别为, ,AN与BM的交点为在x轴上. …………(8分)

②当AB不垂直于x轴时,设直线AB的方程为,

代入椭圆,得

设, , 则, ,

且…………(10分)

∵直线AN方程是, 直线BM方程是.

联列, 得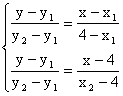, 消去y, 得: .

即 即, ……(12分)

把代入直线AN的方程　　

得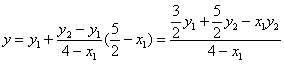

∴AN与BM交于点是x轴上一定点. …………(14分)

(2) 解法二: 如图(2)

设AF＝n, 则AM＝2n, 设BF＝m, 则BN＝2m,

在△ABN和△BAM中, FH∥AM, FH₁∥BN,

∴△ABN∽△AFH和△BAM∽△BFH₁

∴,…………(10分)

同理可推,

∴, …………(12分)

∴,∴H与H₁重合∴AN与BM交点是x轴上一定点. …………(14分)

23、（本小题满分14分）

（1）解： PA－PB=2　　　　  ∴点P的轨迹是以A、B为焦点，焦距为4，实轴长为2的双曲线的右支，其方程为……（4分）

（2）若直线PQ的斜率存在，设斜率为k，则直线PQ的方程为y=k(x－2)代入双曲线方程，得(3－k²)x²+4k²x－4k²－3=0，由

△>0

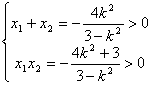解得k²>3，……（6分）

∴PQ=…（8分）

当直线斜率不存在时x₁=x₂=2，得y₁=3，y₂=－3，PQ=6，PQ的最小值为6　　……（10分）

（3）当PC⊥CQ时，P、C、Q构成直角三角形

∴R到直线l的距离　　　　　　　　　①

又∵点P、Q都在双曲线上，

∴，

∴即PQ=4x_R－2，∴②

将②代入①得，PQ=2－4a≥6，

故有a≤－1……（14分）