通江中学高2007级第四学期中期考试

数　学　试　题　（理）

　　　　　　　　　（120分钟完卷，总分150分）　　　　　命题者：徐荣德

一、选择题（本大题共12小题,每小题5分,共60分）

1．经过空间任意三点的平面 （　　）

　　A　只有一个　　　　　　　　　　　　 B　有二个 　　　　

　　C　有无数多个　　　　　　　　　　　 D　只有一个或有无数多个

2．在正多面体中没有（　　　）

A　正六面体　　　 B　正八面体　 　　C　正十二面体　　　 D　正十六面体

3．由0，1，2，3组成的无重复数字的四位数一共有 （　　）

A　6个　　 　　　B　18个　　　　 　C　24 个　　　 D　28个

4．已知α，β是平面，m、n、是直线.下列命题中不正确的是　　  （　　 ）

　　A　若m∥n，m⊥α，则n⊥α　　　 B　若，则m∥n

　　C　若m⊥α，m⊥β，则α∥β　　　D　若m⊥α，，则α⊥β

5、在正方体中，点为棱上的一动点，则与所成的角为（　  ）

　　A　随点的变化而变化　　 　B　45°　　 C　　 　D　

6、若，则=（　 　）

A　31　　　 B　1  　 　 　C　－1 　　　 D　－31

7、在三棱柱的9条棱中异面直线共（　 　）

　　A　36对　　 B　24对　　C　12对　　　　D　6对

8、先后抛掷2枚均匀的硬币，出现“一枚正面，一枚反面”的概率是（　　　）

　　A　　　　B　　　　　C　　　　　D　

9．某人射击1次，命中目标的概率是0.6，他连续射击若干次，若规定命中目标两次后便停止射击，则此人射击3次后停止射击的概率是（　　　）

　　A　0.432　　　　B　0.288　　　　C　0.144　 　D　0.096　

10．学校高中二年级新来了4名同学，要把这4名同学分到高二的1、2、3班3个班去，每班至少1人，不同的分法共有（　 　）

A　72种　　　B　36种　　 C　24种　　　 D　12种

11．如图，在正三棱锥中，E、F分别是AB、BC的中点，且，若，则正三棱锥的体积为（　　　）

A　　　　B　　　

C　　　　D　

12．正方形ABCD的边长为6 cm，点E在AD上，且AE＝AD，点F在BC上，且BF ＝BC，把正方形沿对角线BD折成直二面角A－BD－C后，则EF ＝　（　 　）

　　A．2cm 　　　 B．2cm　　　 C． 2cm　　　 D．6 cm

二、填空题（本大题共4小题，每小题4分，共16分）

13、设地球半径为R，在南纬30°圈上有A、B两点，这两点的经度差为π，则A、B两点的球面距离为　　　　　　 ；

14．已知 的展开式中第二项与第九项的二项式系数相等，则的展开式中的系数是　　　　　　　　；

15．某单位有7个连在一起的停车位，现有3辆不同型号的车需要停放，如果要求剩余的4个空车位连在一起，则不同的停放方法有 　　　　　　　　种（用数字作答）　；　　　

16．在正方形中，过对角线的一个平面交于E，交于F，则

①　  四边形一定是平行四边形

②　  四边形在底面ABCD内的投影一定是正方形

③　  四边形有可能是正方形

④　  四边形有可能垂直于平面

以上结论正确的为　　　　　　　　。（写出所有正确结论的编号）

通江中学高2007级第四学期中期考试

数　学　答　题　卷

一、选择题（每小题5分，共60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题（每小题4分，共16分）

13、　　 　　　　　　　　　　 　；　 　14、　　　 　　　　　　　　 ； 

15、　　　　　 　　　　　　　   ；　　16、　　　　　　　　　　　 　 。

三、解答题：（本大题共74分．解答应写出必要的文字说明、证明过程及演算步骤。）

17、（12分）有5个男生和3个女生，从中选出5人担任5门不同学科的科代表，求分别符合下列条件的选法数：

（1）女生2人男生3人；

（2）男生甲必须包括在内，但不担任数学科代表。

18、（12分）已知正方体的棱长为2，E是的中点。

　（1）求直线与平面所成的角；

（2）求异面直线与间的距离。

19、（12分）已知：甲袋中有3个黑球，2个白球；乙袋中有4个黑球，3个白球.

（1）从甲袋中任意取出两个球，求取得一黑球一白球的概率；

（2）从乙袋中任意取出三个球，求至少取得两个黑球的概率；

（3）从甲、乙两袋中分别取出一个球，求取得一黑球一白球的概率.

20、（12分）甲、乙两人各进行3次射击，甲每次击中目标的概率为，乙每次击中目标的概率。

　（1）求甲恰好击中目标1次的概率；

　（2）求乙至少击中目标1次的概率；

　（3）求乙恰好比甲少击中目标2次的概率．

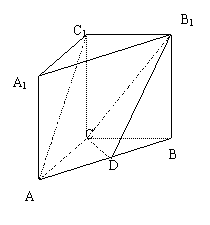21、（12分）　如图, 在直三棱柱ABC－A₁B₁C₁中，AC＝3，BC＝4，,AA₁＝4，点D是AB的中点，

　（1）求证：AC ₁//平面CDB₁；

　（2）求异面直线 AC₁与 B₁C所成角．

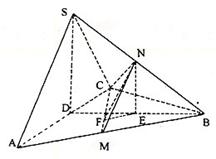
22.(14分)在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，

SA=SC=2，M、N分别为AB、SB的中点。

（1）求证：AC⊥SB；

（2）求二面角N-CM-B的大小；

（3）求点B到平面CMN的距离。

通江中学高2007级第四学期中期考试

数学试题参考答案及评分标准

一、选择题（每小题5分，共60分）

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案	D	D	B	B	D	A	C	C	B	B	C	A

二、填空题（每小题4分，共16分）

13、 ； 　　14、　－ ；　15、24；　　16、  ①②④。

三、解答题：（本大题共74分．解答应写出必要的文字说明、证明过程及演算步骤。）

17、解：(1)（种）；（6分） (2) 3360（种）。（12分）

18．（1）（6分）（2）2（12分）

19．解：（1）从甲袋中任取两球的总数为C₅²=10，取得一黑一白的总数为C₃¹·C₂¹=6，

所求的概率为P₁==.（4分）

（2）从乙中任取三球，至少取得两个黑球的概率。（8分）

（3）甲袋中任意取出黑球的概率为，取出白球的概率为；乙袋中取出黑球的概率为，取出白球的概率为.因此所求概率P₃=·+·=.（12分）

20．解：（1）甲恰好击中目标的1次的概率为； （4分）

　　　（2）乙至少击中目标1次的概率为；（8分）

　　　（3）设乙恰好比甲少击中目标2次为事件A，乙恰击中目标0次且甲恰击中目标2次为事件B₁，乙恰击中目标1次且甲恰击中目标3次为事件B₂，则A＝B₁＋B₂，B₁，B₂为互斥事件．

.

 　 所以，乙恰好比甲少击中目标2次的概率为.（12分）

21．解法一：（1）连结CB₁与C₁B相交于E，连结DE，

∵ D是AB的中点，E是BC₁的中点，

∴ DE//AC₁，

∵ DE平面CDB₁，AC₁平面CDB₁，

∴ AC₁//平面CDB₁；（6分）

（2）∵ DE//AC₁，∴ ∠CED（或其补角）为AC₁与B₁C所成的角，

在△CED中，ED=AC ₁=，CD=AB=，CE=CB₁=2，

∴ ，

∴ 异面直线 AC₁与 B₁C所成角的为.（12分）

解法2：（向量法）略

22、解法一：（1）取AC中点D，连结SD、DB。

∵SA=SC，AB=BC，∴AC⊥SD且AC⊥BD，

∴AC⊥平面SDB，又SB平面SDB，

∴AC⊥SB.（4分）

（2）∵AC⊥平面SDB，AC平面ABC，∴平面SDB⊥平面ABC.

过N作NE⊥BD于E，NE⊥平面ABC，过E作EF⊥CM于F，连结NF，则NF⊥CM.

∴∠NFE为二面角N-CM-B的平面角.

∵平面SAC⊥平面ABC，SD⊥AC，∴SD⊥平面ABC.

又∵NE⊥平面ABC，∴NE∥SD.

∵SN=NB，∴NE=SD===，且ED=EB.

在正△ABC中，由平几知识可求得EF=MB=，

在Rt△NEF中，tan∠NFE==2，

∴二面角N-CM-B的大小是arctan2.（10分）

（3）在Rt△NEF中，NF==，

∴S_△CMN=CM·NF=，S_△CMB=BM·CM=2.

设点B到平面CMN的距离为h，

∵V_B-CMN=V_N-CMB，NE⊥平面CMB，

∴S_△CMN·h=S_△CMB·NE，

∴h==.

即点B到平面CMN的距离为.（14分）

解法二：（1）取AC中点O，连结OS、OB.

∵SA=SC，AB=BC，

∴AC⊥SO且AC⊥BO.

∵平面SAC⊥平面ABC，平面SAC∩平面ABC=AC

∴SO⊥面ABC，∴SO⊥BO.

如图所示建立空间直角坐标系O-xyz.

则A（2，0，0），B（0，2，0），C（-2，0，0），

S（0，0，2），M(1，，0)，N(0，，).

∴=（-4，0，0），=（0，2，2），

∵·=（-4，0，0）·（0，2，2）=0，∴AC⊥SB.

（2）由（Ⅰ）得=（3，，0)，=（-1，0，）.

设=（x，y，z）为平面CMN的一个法向量_，

则　取z=1，则x=，y=-，

∴=(，-，1)，又=(0，0，2)为平面ABC的一个法向量，

∴cos(n，)==.

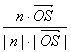∴二面角N-CM-B的大小为arccos.

（3）由（1）（2）得=（-1，，0），=（，-，1）为平面CMN的一个法向量，

∴点B到平面CMN的距离d==.