武汉中学高二下学期数学总复习试题(1)

武汉中学　 柏任俊

一、选择题：

1.设、、为平面，m、n、l为直线，则的一个充分条件是　　　　　　　　（　 ）

　　　 A．　　　　　　 B．

　　　 C．　　　　　　　D．

2.已知△ABC的三个顶点在同一球面上，∠BAC=90°，AB=AC=2. 若球心O到平面ABC

　 的距离为1，则该球的半径为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ 　）

　　　 A．1　　　　　　　　　　　　B．　　　　　　　　　　C．　　　　　　　　　　D．2

3.在正三棱锥中，，分别是棱、的中点，且，若侧棱，则正三棱锥外接球的表面积是　　　　　　　　　　　　　  （　 ）

A．　　　　　　　　　 B．　　　　　　　  C．　　　　　  D．

4.已知展开式中的常数项为1120，其中实数式常数，则展开式中各项系数的和为（　 ）

A．　　　　　　　　　 B．　　　　　　　　 C．1或　　　　 D．1或

5.在二项式的展开式中，存在着系数之比为5：7的相邻两项，则指数n（n）的最小值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

　 A. 13　　　　　　　　 B.　 12　　　　　  C.　　 11　　　　  D.10

6.定义nk = ia_k ＝ a_i＋ a_i＋1 ＋ a_i＋2 ＋…＋ a_n ，其中i、n∈N_＋，且i≤n，

若f (x) ＝ 2003k = 0(－1)^k (3－x)^k ＝ 2003i = 0 a_i x^{2003 － i}，则2003k = 1a_k的值为　 　　　　　　（ 　）

A．2　　　　B．0　　　　C．－1　　　　D．－2

7.某校需要在5名男生和5名女生中选出4人参加一项文化交流活动，由于工作需要，男生甲与男生乙至少有一人参加活动，女生丙必须参加活动，则不同的选人方式有　　　 （ 　）

　　　 A．56种　　　　　　　　　B．49种　　　　　　　　　C．42种　　　　　　　　　D．14种

8.以平行六面体的任意三个顶点为顶点作三角形，从中随机取出两个三角形，则这两个三角形不共面的概率为　　　　　　　　　　　　　　　　　　　  （　 ）

A、　　　　 B、　　　 C、　　  D、

9.老师为研究男女同学数学学习的差异情况，对某班50名同学（其中男同学30名，女同学20名）采取分层抽样的方法，抽取一个样本容量为10的样本进行研究，某女同学甲被抽到的概率为　　　　　　　　　　　　　　　　　　　　　　　　　　　　  　　　　 （　 ）

A．　　　　　　  B．　　　　　　 C．　　　　　　　  D．

10.垂直于直线，且与曲线相切的直线方程是　　 　　（　 ）

A．　B．　C．　D．

二、填空题：

11.一个底面边长为2cm，高为cm的正三棱锥，其顶点位于球心，底面三个顶点位于球面上，则该球的体积为 　　　　　  

12.已知n∈N^* ，多项式P(x)== a₀+a₁x+a₂x²+---+a_nx ⁿ ，则a _n=________.

13.雅典奥运会的第三天共产生8枚金牌，分别为中国4枚，美国2枚，日本、希腊各一枚，在奏国歌的先后顺序中，奏希腊国歌的前后都是奏中国国歌，美国国歌不连在一起奏的，则这天奏国歌的不同顺序________种.

14.某班有男、女生各20人，在一次数学测验中，男生的成绩统计分析得均分为95，标准差为6；女生成绩统计分析得均分为85，标准差为4．则全班统计分析得均分和标准差分别为　　　　　　　　　　　　　　　  ．

15.设P是曲线 y＝x³－x＋上任意一点，点P处切线的倾斜角为α，则α的取值范围是　　　　　　　　　 ．

16.已知函数，若的单调减区间是 （0，4），则在曲线的切线中，斜率最小的切线方程是_________________.

三、解答题：

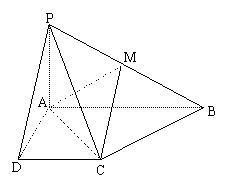
17.已知四棱锥的底面是直角梯形，底面ABCD，是PB的中点.（I）证明：平面平面PCD；（II）求AC与PB所成的角；（III）求平面AMC与平面BMC所成角的大小.

18.如图，在几何体ABCDE中，△ABC是等腰直角三角形，∠ABC ＝90⁰，BE和CD都垂直于平面ABC，且BE＝AB＝2，CD＝1，点F是AE的中点.（Ⅰ）求证：DF∥平面ABC；（Ⅱ）求二面角B－AD－C的大小；（Ⅲ）求AB与平面BDF所成角的大小．

19.美国篮球职业联赛(NBA)某赛季在湖人队与活塞队之间进行，比赛采取七局四胜制，即有一队胜四场，则此队获胜且比赛结束.因两队实力非常接近，在每场比赛中每队获胜是等可能的. 据资料统计，每场比赛组织者可获门票收入100万美元. 问：

（1）　　　　　 组织者在此次决赛中获门票收入恰为400万美元的概率为多少?

（2）　　　　　 组织者在此次决赛中获门票收入不少于600万美元的概率是多少?

20. 高三（1）班50名学生在元旦联欢时，仅买了甲、乙两种饮料可供饮用，在联欢会上甲饮料喝掉了36瓶，乙饮料喝掉了39瓶，假设每个人至多喝一瓶甲饮料和一瓶乙饮料，并且有5名学生两种饮料都没有喝，随机选取该班的一名学生，计算下列事件的概率

（1）　　　 他没有喝甲饮料；

（2）　　　 他喝了1瓶乙饮料但是没有喝甲饮料；

（3）　　　 他喝了1瓶甲饮料和1瓶乙饮料。

21.设函数f（x）= aR.（1）当a =1时，求证f(x)为单调增函数；

（2）当x[1,3]时，f (x)的最小值为4，求a的值。

参考答案：

DCCCC  DBACA　11.【答案】；12.【答案】；13.【答案】120；

14.【答案】90；；15.【答案】[0，）∪[，π）；16.【答案】.

17.解：方法一：（I）证明：底面，

由三垂线定理得，则平面PAD，平面平面PAD.

（II）解：过点B作，且，则是AC与PB所成的角.

与底面ABCD所成的角.

则

又

是等腰直角三角形，

 则与PB所成的角为

（III）解：作，垂足为N，连接BN.在直角中，又

得则是所求二面角的平面角.

，得面PAC，

在直角中，，所以

在等腰中用等积变换，

则所求的二面角为

方法二：底面ABCD，构成空间坐标系，各点坐标是

（I）证明：，由得

　　　  由得则平面PAD. 所以平面平PAD.

（II）解：

　　　 所以AC与PB所成的角为

（III）解：在MC上取一点，则，

　　　  ，要使，则需

　　　  即，解得由得，则N点坐标为　　　 从而为　　 所求二面角的平面角。

　　　  所以所求二面角为

18.【答案】（Ⅱ）arctan3；（Ⅲ）arcsin.

19.

20.

21.解：（Ⅰ）当a=1时，f (x)=，f ′(x)=，

∴， 故f (x)为单调增函数．

　　（Ⅱ）f ′(x)=．

（1）当a≤1时，f (x) 在区间[1，3]上是单调增函数，最小值为f (1)．

由于f (1)=4，即．解得（舍去）．

（2）当时，f (x)在区间（1，a）上是减函数，在区间（a，3）上是增函数，故f (a)为最小值．f (a)=4，即．解得　（舍去），．

（3）当a≥3时，f (x)在区间（1，a）上是减函数，f (3)为最小值．

f (3)=4，即．解得（舍去）．

综上所述，．