武汉中学高二下学期数学总复习试题(6)

武汉中学　 柏任俊

一、选择题：

1.已知棱长为的正四面体有内切球，经过该棱锥的中截面为，则到平面的距离为　　　　　　　　　　　　　　　　　　　　　　　　　　　　  （　 ）

A．　　　　　　　　　  B．　　　　　　　  C．　　　　  D．

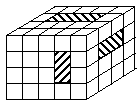
2.如图所示是一个的5×4×4的长方体，上面有2×1×4、2×1×5、　3×1×4穿透的三个洞，那么剩下部分的体积是（　 ）

A．50　　　B．54　　　C．56　　　D．58

3.已知线段AD//平面，且与平面的距离等于4，点B是平面内动点，且满足AB=5,AD=10,则B、D两点之间的距离　　　　　　　　　　　　　　　　　 　　　　　　　　　（　 ）

A. 有最大值，无最小值　　　　B. 有最小值，无最大值

C. 有最大值，最小值　　  D. 有最大值，最小值 　　 

4.（x -1）⁵+5（x -1）⁴+10（x -1）³+10（x -1）²+5(x -1)等于　　　　　　　  （　 ）

A．　　　　 B．　　　　  C．　　　　 D．

5.使得C_n¹+2C_n²+3C_n³+…+nC_nⁿ＜2003不成立的最小的正整数n的值为　　　　　　  （ 　）

A、11　　　　　 B、10　　　　C、9　　　　 D、8

6.在某次乒乓球单打比赛中，原计划每两名选手恰好比赛一场，但有3名选手各自比赛了2场就退了下来，这样，全部比赛只进行了50场，那么上述3名选手之间比赛的场数是 （　 ）

A．0　　　　　　　　　　 B．1　　　　　　　　　　 C．2　　　　　　　　　　 D．3

7.已知直线(不全为)与圆有公共点,且公共点的横、纵坐标均为整数,那么这样的直线有　　　　　　　　　　　　　　　　　　　　　　　  　（　 ）

A.66条　　　　B.72条　　　　　  C.74条　　　　　　　 D.78条

8.要从10名女生与5名男生中选取6名学生组成课外兴趣小组，如果按性别分层随机抽样，试问组成课外兴趣小组的概率是　　　　　　　　　　　　　　　　　 　　　　　 （　 ）

A．　　　 B．　　　　 C．　　　　 D．　　　　　　　　

9.箱子里有5个黑球，4个白球，每次随机取出一个球，若取出黑球，则放回箱中，重新取球，若取出白球，则停止取球，那么在第4次取球之后停止的概率为　　　 　　　　　　  （　 ）

　　　 A．　　　　 B．　　　 C．　　 　D．

10.设函数f(x)在定义域内可导，y= f(x)的图象如右图所示，则导函数y= f′(x)的图象可能为　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （ 　）

　　　　　　

二、填空题：

11.在正方体中，过对角线的一个平面交于，交于F，则：①四边形一定是平行四边形；②四边形有可能是正方形；③四边形在底面内的投影一定正方形；④四边形有可能垂直于平面.

以上结论正确的是　　　　　　　　 .（写出所有正确结论的编号）

12.正四棱锥P－ABCD的底面ABCD在球O的大圆面上，顶点P在球面上，已知球的体积为，则正四棱锥P－ABCD的体积的最大值为　　　　　　 .

13.已知的展开式中，所有项的系数之和等于81，那么这个展开式中的系数是

　　　　　.

14.从装有个球（其中个白球，1个黑球）的口袋中取出个球,共有种取法。在这种取法中，可以分成两类：一类是取出的个球全部为白球，共有，即有等式：成立。试根据上述思想化简下列式子：　　　　..

15.有一组数据：的算术平均值为10，若去掉其中最大的一个，余下数据的算术平均值为9；若去掉其中最小的一个，余下数据的算术平均值为11，第一个数关于的表达式是__________，第个数关于的表达式是___________.

16.设函数f(x)=k+3(k-1)+1在区间（0，4）上是减函数，则k的取值范围是　　　 .

三、解答题：

17.在三棱柱中，侧面底面，且.（1）求证：平面平面；（2）求异面直线与所成的角。

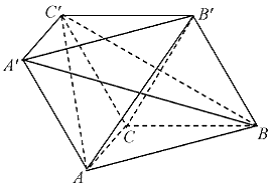
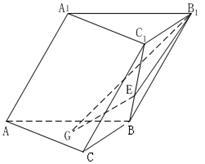
18.如图，在斜三棱柱ABC－A₁B₁C₁中，侧面AA₁B₁B⊥底面ABC，侧棱AA₁与底面ABC成60⁰的角， AA₁= 2．底面ABC是边长为2的正三角形，其重心为G点。E是线段BC₁上一点，且BE=BC₁ ．（１）求证： GE∥侧面AA₁B₁B ；（２）求平面B₁GE与底面ABC所成锐二面角的大小 ．

19. 甲、乙、丙三台机床各自独立地加工同一种零件，已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为,甲、丙两台机床加工的零件都是一等品的概率为.（Ⅰ）分别求甲、乙、丙三台机床各自加工零件是一等品的概率；（Ⅱ）从甲、乙、丙加工的零件中各取一个检验，求至少有一个一等品的概率。

20.杨辉是中国南宋末年的一位杰出的数学家、数学教育家．他的数学著作颇多，他编著的数学书共五种二十一卷，在他的著作中收录了不少现已失传的古代数学著作中的算题和算法．他的数学研究与教育工作的重点是在计算技术方面．杨辉三角是杨辉的一大重要研究成果，它的许多性质与组合数的性质有关．杨辉三角中蕴涵了许多优美的规律．古今中外，许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都曾深入研究过，并将研究结果应用于其他工作．下面是一个11阶的杨辉三角：

试回答：（其中第（1）~（4）小题只须直接给出最后的结果，无须求解过程．）

（1）记第i（i∈N*）行中从左到右的第j（j∈N*）个数为，则数列{}的通项公式为　　　　　　　　　 ；n阶杨辉三角中共有　　　　　　　 个数．

（2）第k行各数的和是　　　　　　　　　　　  ．

（3）n阶杨辉三角的所有数的和是　　　　　　　　　　　  ．

（4）第p（p∈N*，且p≥2）行除去两端的数字1以外的所有数都能被p整除，则整数p一定为　　　　　  ．A．奇数　　 B．质数　　　C．非偶数　　　 D．合数

（5）在第3斜列中，前5个数依次为1、3、6、10、15；第4斜列中，第5个数为35．显然，1+3+6+10+15=35．事实上，一般地有这样的结论：

第m斜列中（从右上到左下）前k个数之和，一定等于第m+1斜列中第k个数．

试用含有m、k（m、k∈N*）的数学公式表示上述结论并证明其正确性．

数学公式为：　　　　　　　　　　　　　　　　　　　　　　　　　　　   ．

21.设函数 （a、b、c、d∈R）图象关于原点对称，且x=1时，取极小值（1）求a、b、c、d的值；（2）当时，图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论；（3）若时，求证：.

参考答案：

CCDBC　BBABD　

3.〖解〗V＝80－(8＋10＋12)＋(2＋3＋2)－1＝56，选C.

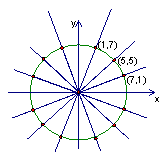7.提示：先考虑时,圆上横、纵坐标均为整数的点有、、，依圆的对称性知,圆上共有个点横纵坐标均为整数,经过其中任意两点的割线有条,过每一点的切线共有12条,又考虑到直线不经过原点,而上述直线中经过原点的有6条，所以满足题意的直线共有条,故选B.

11.【答案】①③④；12.【答案】16 / 3；13.【答案】32；14.【答案】；根据题中的信息，可以把左边的式子归纳为从个球（n个白球，k个黑球）中取出m个球，可分为：没有黑球，一个黑球，……，k个黑球等类，故有种取法。

15.【答案】；.16.【答案】.

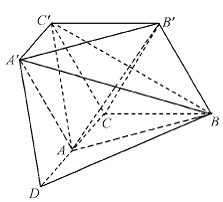17.解法一　（1）平面平面，，平面　　　　　　　　　　　　　  　　　　　　　　　　　 

在中，为菱形。

平面.　　　　　　　　　　　　　　　　　　　 

又平面平面平面.

（2）延长到，使，连

为平行四边形。

为异面直线与所成的角。

设平面在菱形,

又从而在中，

 异面直线与所成的角的大小为.

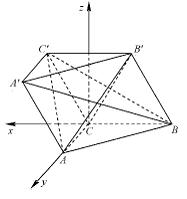
解法二　建立如图所示的空间直角坐标系。设

则，

则

，

（1），平面.

又平面，平面平面.

（2）.

.

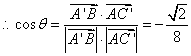异面直线与所成的角为.

18.解：(1)延长B₁E交BC于F,∵ΔB₁EC∽ΔFEB,BE＝ＥＣ₁

∴ＢＦ＝Ｂ_１Ｃ_１＝ＢＣ，从而Ｆ为ＢＣ的中点．　　

∵Ｇ为ΔＡＢＣ的重心，∴Ａ、Ｇ、Ｆ三点共线，

且＝　 ＝，∴GE∥AB₁，又GE侧面AA₁B₁B， ∴GE∥侧面AA₁B₁B.

（２）在侧面AA₁B₁B内，过B₁作B₁Ｈ⊥ＡＢ，垂足为Ｈ，∵侧面AA₁B₁B⊥底面ABC，

∴B₁Ｈ⊥底面ABC．又侧棱AA₁与底面ABC成60⁰的角， AA₁= 2，

∴∠B₁ＢＨ＝６０^０，ＢＨ＝１，B₁Ｈ＝．

在底面ABC内，过Ｈ作ＨＴ⊥ＡＦ，垂足为Ｔ，连B₁Ｔ．由三垂线定理有B₁Ｔ⊥ＡＦ，

又平面B₁GE与底面ABC的交线为ＡＦ，∴∠B₁ＴＨ为所求二面角的平面角．

∴ＡＨ＝ＡＢ＋ＢＨ＝３，∠ＨＡＴ＝３０^０，　∴ＨＴ＝ＡＨsin30⁰＝，

在ＲｔΔB₁ＨＴ中，ｔａｎ∠B₁ＴＨ＝＝　，

从而平面B₁GE与底面ABC所成锐二面角的大小为arctan.

19.

20.解：（1）；；（2）2^k ；（3）；（4）B．

（5）．

证明　

．

21.解（1）∵函数图象关于原点对称，∴对任意实数，

，即恒成立

　，

时，取极小值，解得

　 （2）当时，图象上不存在这样的两点使结论成立.

假设图象上存在两点、，使得过此两点处的切线互相垂直，

则由知两点处的切线斜率分别为，

且　　  （ *）

、，

此与（*）相矛盾，故假设不成立.

证明（3），

或，

上是减函数，且

∴在[－1，1]上，时，

.