四川省遂宁市高2007级第三学期期末学科知识检测
数 学 试 题（理科）
注意事项：
1、本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。总分150分，考试时间120分钟。
2、答第Ⅰ卷前，考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上；
3、每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦擦干净后，再选涂其它答案，不能答在试卷了；
4、考试结束后，将答题卡和第Ⅱ卷交回；
5、未使用答题卡的学校，请考生用钢笔或圆珠笔将所选答案的字母代号填写在第Ⅱ卷前面选择题答题表对应题目的空格中。
第Ⅰ卷（选择题 共60分）
一、选择题：本大题共12个小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。
1、以P（2 , 3 ）为圆心，并且和直线x + y－3 = 0相切的圆的方程为
A、
B、
C、
D、
2、三条直线两两相交所确定的平面个数是
A、三个 B、两个 C、一个 D、一个或三个
3、椭圆 
的焦距为2，则m的取值是
A、5 B、5或8 C、3或5 D、20
4、椭圆短轴长是2，长轴长是短轴长的2倍，则椭圆中心到其准线距离是
A、
B、
C、
D、
5、动点P到定点F1（ 1 , 0 ）的距离比它到定点F2（3，0）的距离小2，则点P的轨迹是
A、双曲线 B、双曲线的一支 C、一条射线 D、两条射线
6、椭圆
上一点P到其右准线的距离为10，则该点到其左焦点的距离是
A、8 B、10 C、12 D、14
7、（理）已知方程
表示椭圆，则双曲线
的焦点坐标是
A、（±
，0）
B、（±
，0）
C、（0，±）
D、（0，±）
8、已知一个简单多面体的各个顶点都有三条棱，则顶点数V与面数F满足的关系正确的是
A、2F + V＝4 B、2F－V＝4 C、2F + V＝2 D、2F－V＝2
9、空间四边形ABCD中，AC＝BD，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH是
A、菱形 B、矩形 C、梯形 D、正方形
10、一个与球心距离为1的平面截球所得的圆面面积为π，则球的表面积为
A、8 B、8π C、4 D、4π
11、椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆壁反射后，反射光线经过椭圆的另一个焦点，今有一个水平放置的椭圆形台球盘，点A、B是它的焦点，长轴长为2a，焦距为2c，静放在点A的小球（小球的半径不计），从点A沿直线出发，经椭圆壁反弹后第一次回到点A时，小球经过的路程是
A、4a B、2（a－c ） C、2（a + c） D、以上答案均有可能
12、（理）设抛物线的顶点在原点，其对称轴是一条坐标轴，且焦点在直线2x－y + 4 = 0上，则此抛物线方程是
A、y2 = －8x B、x2 = 16y
C、y2 = －8x或x2＝16y D、y2 = 8x或x2 = 16y
第Ⅱ卷（非选择题 共90分）
一、选择题（本大题共12个小题，每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（本大题共四个小题，每小题4分，共16分，把答案填在题中横线上）
13、已知圆C1：（x + 1）2 +（y －3）2 = 9，圆C2：x2 + y2－4x + 2y－11 = 0，则两圆公共弦所在直线方程为________________________。
14、三棱锥的三个侧面两两垂直，它们的面积分别为6，4，3，则三棱锥的体积为________________________。
15、若椭圆
的弦被点（4，2）平分，则此弦所在直线的斜率为____________________。 16、给出下面四个命题：①“直线a、b为异面直线”的充分非必要条件是“直线a、b不相交”；②“直线ι垂直于平面a内所有直线”的充要条件是“ι⊥平面a”；③“直线a⊥b”的充分非必要条件是“a垂直于b在平面a内的射影”；④“直线a∥平面β”的必要非充分条件是“直线a至少平行于平面β内的一条直线”.其中正确的命题是________________________。
三、解答题（本大题共6个小题，满分74分。解答应写出文字说明、证明过程或演算步骤）
17、求与椭圆
有共同的焦点，且离心率
的双曲线方程。
18、求与圆x2 + y2 + 8x + 6y = 0相切，且在两坐标轴上的截距相等的切线方程。
19、如图：已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点
（1）求证：MN∥平面PAD；
（2）求异面直线MN与CD所成的角的大小；
（3）若∠PDA＝45°，求证：MN⊥平面PCD。
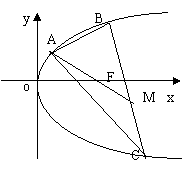
20、已知点A（2、8），B（x1 , y1 ），C（x2 , y2）在抛物线y2＝2Px上，△ABC的重心与抛物线的焦点F重合，如图：
（1）写出该抛物线的方程和焦点坐标；
（2）求线段BC中点M的坐标；
（3）求BC所在直线方程。
21、已知斜三棱柱ABC－A1B1C1的各棱长均为2，侧面与底面所成角为
，顶点B1在底面ABC上的射影D在AB上。
（1）求证：侧面ABB1A1⊥底面ABC；
（2）求证：B1C⊥AB；
（3）求：二面角B1－BC－A的大小。
22、已知椭圆M的两焦点坐标分别为F1（－1，0），F2（1，0），离心率
，P是椭圆M上的动点。
（1）求椭圆M的方程；
（2）设｜
｜－｜
＝m，求m的取值范围；
（3）求
的取值范围。
数学试题参考解答
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | C | D | C | C | C（文） D（理） | B | A | B | D | B（文） C（理） |
二、填空题
13、
14、4 15、
16、②④
三、解答题
17、由题意，双曲线的焦点为（5，0），（－5，0），……………………………………2分
又双曲线的离心率e=
∴
………………………………………………10分
∴所求双曲线的方程是
……………………………………………………12分
18、∵
∴圆心坐标是（－4,－3）半径为5……………………2分
圆切线在两坐标轴上截距相等，设截距为a，
①
当
时，则切线方程为
即x+y－a=0
由
，得
故切线方程为：
…………8分
②
若a=0，则切线方程为y=kx，即kx－y=0由
，得
，即
综上，所求切线方程为：或…………………………12分
19、证明；（1）取PD的中点E，连AE、EN，则EN
CDABAM，
故AMNE为平行四边形。……………………………………………………………………3分
∴MN∥AE，又AE
平面PAD，MN
平面PAD∴MN∥平面PAD…………………………6分
（2）解：∵ PA
平面ABCD ∴ PAAB，
又ADAB ∴ AB平面PAD ∴ABAE，……………………………………………9分
又AE∥MN ∴ ABMN，又CD∥AB ∴ MNCD
∴异面直线MN与CD所成的角为900。…………………………………………………12分
20、解：（1）由点A（2，8）在抛物线
上，有
，解得p=16，所以抛物线方程为y2=32x，焦点F的坐标为（8，0）。………………………………（4分）
（2）由F（8，0）是
的重心，M是BC的中点，∴F是线段AM的定比分点，且
，设点M的坐标为
，则
解得x0=11,y0=－4
∴点M的坐标为(11,－4) …………………………………………………（8分）
（3）由于线段BC的中点M不在x轴上，所以BC所在直线不垂直于x轴，设BC所在直线的方程为y+4=k(x－11) (k≠0)由
消去x得，
∴
由（2）的结论得
∴
∴k=－4∴BC所在直线方程为y+4=－4(x－11)即4x+y－40=0……………………（12分）
21、解：（1）证明：依题意，∵B1D平面ABC，B1在面ABB1A1内
∴面ABB1A1面ABC ……………………………………………………………4分
（2）连结CD，∵B1D面ABC，∴
∴BD=B1Bcos=1,
即D为AB的中点…………………………………………………………………………6分
∴CDAB，又ABB1D，
，∴
又
∴
………………………………………………………………………………8分
（3）作DEBC于E，连B1E，则由三垂线定理可知，B1EBC
∴
为二面角B1—BC—A的平面角…………………………………………………10分
∵ED=
，B1D=
∴tan
∴
即二面角B1—BC—A的大小为arctan2。…………………………8分
22、解（1）由已知得：c=1,
∴a=2,b=
即椭圆M的方程为
……………………………………………（4分）
（2）设P点的坐标为，则
，又
∴
…………………………………（9分）
（3）∵
=m, 
∴
，
=
=
=
=
又
…………………………………………………（14分）