苏州市2005-2006学年度第一学期期末考试
高二数学
2006。01。16。
一、选择题:
1、直线![]() 的倾斜角
的倾斜角![]() 等于
( )
等于
( )
A、0
B、![]() C、
C、![]() D、
D、![]()
2、已知圆![]() 与圆
与圆![]() 关于直线
关于直线![]() 对称,则圆
对称,则圆![]() 的方程是
( )
的方程是
( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
3、5名同学排成一排,其中甲不排在正中位置的不同排法有 ( )
A、120 B、24 C、96 D、48
4、某人的密码箱上是一个四位数字的号码,每位上的数字可在0到9这十个数字中选取,开箱时随意按下一个四位数号码,恰好按对密码的概率是 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5、![]() 是方程
是方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线的
( )
轴上的双曲线的
( )
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要
6、抛物线![]() 上一点
上一点![]() 的纵坐标是4,则点
的纵坐标是4,则点![]() 与抛物线焦点的距离为
( )
与抛物线焦点的距离为
( )
A、5 B、4 C、3 D、2
7、在![]() 的展开式中,含
的展开式中,含![]() 的项的系数为
( )
的项的系数为
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8、已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,其长轴长为8,焦点
轴上,其长轴长为8,焦点![]() 到长轴的一个端点的距离为6,则椭圆
到长轴的一个端点的距离为6,则椭圆![]() 的准线方程是
( )
的准线方程是
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、16名同学分别到4个不同的路口进行车流量的调查,若每个路口安排4人,则不同的分配方案共有 ( )
A、![]() 种 B、
种 B、![]() 种 C、
种 C、![]() 种 D、
种 D、![]() 种
种
10、已知![]() 是双曲线
是双曲线![]() 的焦点,过
的焦点,过![]() 作垂直于
作垂直于![]() 轴的直线交双曲线于点
轴的直线交双曲线于点![]() ,若
,若![]() ,则双曲线的渐近线方程为
( )
,则双曲线的渐近线方程为
( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、编号为![]() 六种花种种植在如图所示的六块区域组成的花坛内,要求
六种花种种植在如图所示的六块区域组成的花坛内,要求![]() 号花不能种在1、2、3号区域,
号花不能种在1、2、3号区域,![]() 号花必须与
号花必须与![]() 号相邻,则不同的种植方法共有 ( )
号相邻,则不同的种植方法共有 ( )
A、720 B、192 C、360 D、240
 |
12、过抛物线![]() 上的动点
上的动点![]() 向圆
向圆![]() 引切线,则切线长的最小值是( )
引切线,则切线长的最小值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
二、填空题:
13、已知直线![]() 与直线
与直线![]() 互相垂直,则实数
互相垂直,则实数![]() ____
____
14、若![]() ,则
,则![]() ________
________
15、甲、乙两位体操运动员参加国际比赛,已知甲做完规定动作得满分的概率为![]() ,乙做完规定动作得满分的概率为
,乙做完规定动作得满分的概率为![]() ,则在比赛中他们两人恰有一人得满分的概率是_________
,则在比赛中他们两人恰有一人得满分的概率是_________
16、实数![]() 、
、![]() 满足不等式组
满足不等式组 ,则
,则![]() 的取值范围是__________
的取值范围是__________
17、将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,再向上平移1个单位所得直线
,再向上平移1个单位所得直线![]() 与圆
与圆![]() 相切,则
相切,则![]() _______
_______
18、从![]() 中任取三个不重复的数作为二次曲线
中任取三个不重复的数作为二次曲线![]() 的系数,其中表示焦点在
的系数,其中表示焦点在![]() 轴上的双曲线的条数有___________
轴上的双曲线的条数有___________
三、解答题:
19、求与![]() 轴相切,圆心在
轴相切,圆心在![]() 上,且被直线
上,且被直线![]() 截得的弦长为
截得的弦长为![]() 的圆方程。
的圆方程。
20、袋里装有30个大小相同的小球,其中彩球中有2个红色、5个蓝色、10个黄色、其余为白色
(1)求从袋里取出3个都是相同颜色彩球(无白色)的概率
(2)从袋里任取3个小球,求至少有一个是红球的概率
21、设点![]() ,
,![]() 是给定的两定点,一动点
是给定的两定点,一动点![]() 满足
满足![]()
(1)求动点![]() 的轨迹
的轨迹![]() 的方程
的方程
(2)设![]() ,
,![]() ,
,![]() ,点
,点![]() 是轨迹
是轨迹![]() 上的一动点,直线
上的一动点,直线![]() 与轨迹
与轨迹![]() 的另一个交点为
的另一个交点为![]() ,求直线
,求直线![]() 和
和![]() 交点
交点![]() 的轨迹方程。
的轨迹方程。
22、已知一枚骰子(一种在正方体的六个面上分别标有1,2,3,4,5,6点的玩具)任意地抛掷![]() 次
次
(1)若![]() ,求1点分别出现1次和2次的概率
,求1点分别出现1次和2次的概率
(2)若![]() ,求1点出现多少次的概率最大。(1点出现即1点的正面向上)
,求1点出现多少次的概率最大。(1点出现即1点的正面向上)
23、已知顶点在原点,焦点在![]() 轴上的抛物线
轴上的抛物线![]() 截直线
截直线![]() 所得的弦的中点坐标为
所得的弦的中点坐标为![]()
(1)求抛物线![]() 的方程
的方程
(2)过点![]() ,倾斜角
,倾斜角![]() 的直线与抛物线
的直线与抛物线![]() 相交于
相交于![]() 两点,求点
两点,求点![]() 分
分![]() 所成比
所成比![]() 的取值范围。
的取值范围。
参考答案
一、选择题:CBCDBA CDADBB
二、填空题:![]() ,
,![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ; 36
; 36
三、解答题:
19、解:设所求圆的方程为![]() ,由条件知
,由条件知![]() ,
,![]()
![]() ,
,![]() ,
,![]()
所求圆方程为![]() 或
或![]()
20、解(1)设从袋里30个球中取出3个都是蓝色球为事件![]() ,取出都是黄色球为事件
,取出都是黄色球为事件![]() ,则取出相同颜色彩球(无白色)的概率为
,则取出相同颜色彩球(无白色)的概率为![]()
(2)设取到1个红球为事件![]() ,取到2个红球为事件
,取到2个红球为事件![]() ,则至少取出一个红球的概率为
,则至少取出一个红球的概率为![]()
答:取出相同颜色彩球(无白色)的概率为![]() ,至少取出一个红球的概率为
,至少取出一个红球的概率为![]() 。
。
21、解:(1)由题意知:轨迹![]() 是椭圆,
是椭圆,![]() ,
,![]() ,
,![]() ,
,![]() 所求方程为
所求方程为![]()
(2)设点![]() ,
,![]() ,则
,则![]() 代入椭圆方程得:
代入椭圆方程得:
![]() ,
,![]() ,得
,得![]()
代入![]() ,得
,得![]()
又![]() ,
,![]() ,即
,即![]()
![]() ,
,![]() ,代入
,代入![]() ,得
,得![]() ,即为所求的轨迹方程。
,即为所求的轨迹方程。
22、(1)设1点出现1次的事件为![]() ,出现2次的事件为
,出现2次的事件为![]() ,则
,则![]()
![]()
(2)设![]() 为100次抛掷中1点出现
为100次抛掷中1点出现![]() 次的概率,且
次的概率,且![]() 取得最大值
取得最大值
由 ,
, ,
,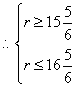 ,
,![]()
答:1点出现1次的概率为![]() ,1点出现2次的概率为
,1点出现2次的概率为![]() ,1点出现16次的概率最大。
,1点出现16次的概率最大。
23、(1)设![]() ,直线与抛物线交于点
,直线与抛物线交于点![]() ,
,![]()
由 ,得
,得![]() ,
,![]() ,
,![]() ,
,![]() 中点为
中点为![]() ,
,![]()
![]() 抛物线方程是
抛物线方程是![]()
(2)设直线![]() ,
,![]()
由 ,得
,得![]() ,
,![]()
![]() ,
,![]() ,由定比分点公式
,由定比分点公式![]() ,即
,即![]()
![]() ,
,![]() ,
,![]() ,
,![]() 的取值范围是
的取值范围是![]()