莆田四中高二上期中考数学(理科)
2005.11.6
一、选择题（每小题5分，共60分）
1．.已知直线l1：(a+1)x+y－2=0与直线l2：ax+(2a+2)y+1=0互相垂直，则实数a的值
为（ ）
A.－1或2 B. 1或2 C. －1或－2 D.1或－2
2．已知点P是直线l：2x-y-4=0与x轴的交点，把直线绕点P按逆时针方向旋转
，得到的直线方程是（ ）
A、
B、
C、
D、
3．若
的两个顶点
坐标分别为
和
，而顶点
在直线
上移动，则
的重心
的轨迹方程是（ ）
， 
4．圆
截
轴所得的弦与截
轴所得的弦的长度之比为 ( )
A. 
B.
C.
D.
5．方程
所表示的曲线图形是（ ）
6．圆
与
轴交于
、
两点，圆心为
，若
，则实数
等于（ ）
1 B -11 C 9 D 11
7．已知F1、F2为双曲线
=1(a＞0,b＞0）的焦点，过F2作垂直于x轴的直线，它与双曲线的一个交点为P，且∠PF1F2=30°，则双曲线的渐近线方程为（ ）
A.y=±
x B.y=±
x C.y=±
x D.y=±
x
8．若直线y＝kx＋2与双曲线
的右支交于不同的两点，则k的取值范围
是（ ）
A．
，
B．
，
C．，
D．，
9．我国发射的“神舟3号”宇宙飞船的运行轨道是以地球的中心
为一个焦点的椭圆，近地点A距地面为m千米，远地点B距地面为n千米，地球半径为R千米，则飞船运行轨道的短轴长为（ ）
A．
B．
C．mn D．2mn
10.直线y=
x+1与曲线
=1的公共点个数为（ ）
A.1 B.2 C.3 D.4
11．设F1、F2为椭圆
+y2=1的两个焦点，P在椭圆上，当△F1PF2面积为1时，
·
的值为( )
A.02 B.1 C.
0 D.
12．E、F是椭圆
的左、右焦点, 
是椭圆的一条准线,点P在上, 则
的最大值是( )
A. 
B. 
C. 
D. 
高二上期中考数学(理科)答案卷
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题（每题4分，共16分）
13.作直线L与圆x2+y2=16交于A、B两点，使△AOB的面积最大(O为原点)，则此
最大值是 。
14..Rt△ABC的斜边AB的长度等于定值C，顶点A、B在x轴，y轴上滑动，则斜边
AB的中点M的轨迹方程为 。
15．椭圆
的离心率为
，则a＝_____ ___．
16．已知直线y＝x＋1与椭圆
（m＞n＞0）相交于A，B两点，若弦AB的中点的横坐标等于
，则双曲线
的两条渐近线的夹角的正切值等于 _ ___
．
三、解答题(6大题,共74分)
17．（本小题满分12分）
已知等腰△ABC中，C=
，直角边BC在直线2x+3y-6=0上，顶点A的坐标是
（5，4），求边AB和AC所在的直线方程。
18．（本小题满分12分）
已知一圆C的圆心为C（2，-1），且该圆被直线L：x-y-1=0截得的弦长为
。
(1)求该圆的方程
(2)求过此弦的两端切线的交点坐标。
19．（本小题满分12分）
北京华欣公司计划在今年内同时出售“夜莺牌多功能”电子琴和“OK智能型”洗衣机，由于这两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况（如资金，劳动力）确定产品的月供应量，以使得总利润达到最大，已知对这两种产品有直接限制的是资金和劳动力，通过调查，得到关于两种产品有关数据如下表：
| 资金 | 单位产品所需资金（百元） | 月资金供应量（百元） | |
| 电子琴 | 洗衣机 | ||
| 成本 | 30 | 23 | 300 |
| 劳动力 | 5 | 10 | 110 |
| 单位利润 | 6 | 8 | |
试问：怎样确定两种产品的月供应量，才能使总利润最大？
20.（本小题满分12分）
已知：双曲线C 中心在原点，焦点在X轴上，离心率e=
，且经过点（2，1）。
（1）求双曲线C的方程。
（2）若点P(2,m)在曲线C上，,过点P引直线l和双曲线C交于P1、P2两点，若P恰
为P1P2的中点，求m的取值范围.
21．（本小题满分13分）
在平面直角坐标系中，长度为6的线段PQ的一个端点P在射线y=0(x≤0)上滑动，另一端点Q在射线x=0(y≤0)上滑动，点M在线段PQ上，且
（Ⅰ）求点M的轨迹方程；
|
22.（本小题满分13分）
设不等边三角形ABC的外心与重心分别为M、G，若A（－1，0），B（1，0）且MG∥AB .
（Ⅰ）求三角形ABC顶点C的轨迹方程；
（Ⅱ）设顶点C的轨迹为D，已知直线l过点（0，1）并且与曲线D交于P、N两点，若O为坐标原点，满足OP⊥ON，求直线l的方程
高二上期中考数学(理科)答案卷
一、选择题（每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | A | A | D | B | D | A | A | B | C | B |
二、填空题（每题4分，共16分）
13.作直线L与圆x2+y2=16交于A、B两点，使△AOB的面积最大(O为原点)，则此
最大值是 8 。
14..Rt△ABC的斜边AB的长度等于定值C，顶点A、B在x轴，y轴上滑动，则斜边
AB的中点M的轨迹方程为 .x2+y2=
(?)
。
15．椭圆的离心率为，则a＝_____
_．
16．已知直线y＝x＋1与椭圆（m＞n＞0）相交于A，B两点，若弦AB的中点的横坐标等于，则双曲线的两条渐近线的夹角的正切值等于____
____．
三、解答题(6大题,共74分)
17．（本小题满分12分）
AC:3X-2Y-7=0 AB:x-5y+15=0 或 5x+y-29=0
18．（本小题满分12分）
(x-2)2+(y+1)2=4
.(0,1)
19．（本小题满分12分）
解析：设电子琴和洗衣机的月供应量分别为
架、台，总利润为
百元，依题意得
即
目标函数
，作出不等式组表示的可行域，如图所示，作直线
即
，把向右上方平移到
的位置，直线过可行域内点M，则直线纵截距最大，
从而对应求出
最大，由
解得
，
当月供应量电子琴4架，洗衣机9台时，该店可获得最大利润为
（百元）
答：略。
20.解：（1）
－y=1
5分
（2）解：设P1(x1,y1)、P2(x2,y2)
由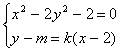
去y得
(1－2k2)x2－4k(m－2k)x－2［(m－2k)2+1］=0, 7分
依题意P(2,m)是P1P2的中点,
∴x1+x2=4,得km=1，①
又Δ＞0,
∴16k2(m－2k)2－4(1－2k2)·（－2）［(m－2k)2+1］＞0
2k2(m－2k)2－(2k2－1)［(m－2k)2+1］＞0,
(m－2k)2－(2k2－1)＞0 8分
由①式有(m－
)2－(
－1)＞0,
m2+
－3＞0,(m2－2)(m2－1)＞0 10分
∴｜m｜＞
或｜m｜＜1,
∴m的取值范围是(－∞,－)∪(－1,1)∪(,+∞).
21．（本小题满分13分）
（I）解：设点P、Q、M的坐标分别是P(x1, 0)、Q（0，y1）、M(x, y) 其中x1≤0，
y1≤0,依条件可得
………………………………………………………2分
又依
代入（*）式，得
即点M的轨迹方程为
……7分
（II）解：设M点的坐标是（4cosα，2sinα）其中0≤α<2π
|
S四边形OAMB=S△OAM+S△OBM
仅当
时，
四边形OAMB的面积有最大值
. …………12分
22.解（Ⅰ）设C（x，y）（xy≠0）.
∵MG∥AB，可设G（a、b），则M（0，b）.
∴x = 3a，y = 3b. ①
∵M是不等边三角形ABC的外心，
∴ MA = MC ，即
②
由①②得 x2
+
,
∴三角形顶点C的轨迹方程为x2 +(xy≠0). （5分）
（Ⅱ）设直线l的方程为y = kx + 1，又设P（x1，y1），N（x2，y2）.
由
消y，得(3 + k2) x2 + 2kx－2 = 0，
∵直线l与曲线D交于P、N两点，
∴b2－4ac = 4k2 + 8(3 + k2)＞0.
又
∵OP⊥ON，
∴x1x2 + y1y2 = 0，
∴x1x2 + (kx1 + 1)(kx2 + 1) = 0,
∴(1+ k2) x1x2 + k(x1 + x2) + 1 = 0,
∴(1+ k2) (
) +
k(
)
+1= 0.
∴k =
∴直线l的方程为y =
x + 1.