深大附中高二复数单元测试题

　　　　　　　　　　　　　　　　　　　　　 　　　 2006.2．26.

　　　　　　　　　　  时间 90分钟　　满分100分

一、选择题：本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的．

1．(1－i)²·i ＝　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）　　A．2－2i　　B．2+2i C． 2　　　　　　 D．－2

2．设复数=　　　　　　　　　　　　　　　　　　　　（　　）

　　A．　　　　　 B．　　　　　　C．　　　　　 D．

3．复数的值是　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．4i　　　　　　 B．－4i　　　　　 C．4　　　　　　　D．－4

4．在复平面上复数i,1,4+2i所对应的点分别是A、B、C,则平面四边形ABCD的对角线BD的长为　(　 )

 (A)5　 　　 (B)　　　 (C) 　　　 (D)

5．复数的值是　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　A．－1　　　　　　B．1　　　　　　　C．32　　　　　　 D．－32

6．复数的值是　　　　　　　　　　　　　　　　　　　　　 (　　) 　　　　　A．－16 B．16　 C．－　D．

7．若复数(m²－3m－4)＋(m²－5m－6)是虚数，则实数m满足（　）

（A）m≠－1　　　　　　（B）m≠6　 

(C) m≠－1或m≠6　　　(D) m≠－1且m≠6

8．已知复数z₁＝3+4i，z₂＝t+i，且是实数，则实数t＝　　　　　　　　　　　　 （　　）

　 A． 　　　　　　B．　　　　　　C．-　　　　　　D．-

9．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　 A．　　　 B．　　C．　　　 D．

10．若且的最小值是　　　　　　　　　　 （　　）

　　A．2　　　　　　　B．3　　　　　　　C．4　　　　　　　D．5

11．复数的共轭复数是　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　A．　　　　 B．　　　　C．　　　　 D．

12．设则　　　　　　　　　　　 （　　　）

深大附中高二复数单元测试题

姓名：　　　　　   学号：　　　　　　 　记分：　　　　　

一. 选择题.(本题共12个小题,每小题5分,共60分)

题号	1	2	3	4	5	6	7	8	9	10	11	12
答案

二、填空题：本大题共4小题，每小题4分，共16分．答案填在题中横线上．

13．实数x、y满足（1–i）x+(1+i)y=2,则xy的值是　　　　  .

14．已知复数z与 (z +2)²－8i 均是纯虚数，则 z = ____________．

15．复数的模为，则实数a的值是　　　　　　　 。

16．在复平面内，是原点，，，表示的复数分别为，那么表示的复数为____________.　

三、解答题：本大题共4小题，共48分．解答应写出文字说明，证明过程或演算步骤．

17．(本小题满分12分)计算

18．(本小题满分12分) 在复平面上，正方形ABCD的两个顶点A，B对应的复数分别为 1+2i，3－5i。求另外两个顶点C，D对应的复数。

19．（本小题满分12分）已知复数z₁满足(1+i)z­₁=－1+5i， z­₂=a－2－i， 其中i为虚数单位，a∈R， 若<z₁，求a的取值范围.

20．（本小题满分12分）已知z、w为复数，（1+3i）z为实数，w=．

　试卷答案

一、1．C 2．C 3．D  4．B  5．A　 6．A　7．D 8．A 9．B　10．B　11．B　12．C

二、13．1　 14．-2i　 15．　　16．4-4i

三、

17．解：

　

18．解：设D（x,y）

由

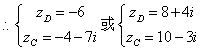
19．解：由题意得 z₁==2+3i，

　于是==，=.

　<，

得a²－8a+7<0，1<a<7.

20．解：设w＝x+yi(x，y∈R)，

依题意得(1+3i)(2+i)w＝(－1+7i)w为实数，且w＝5，

∴，

解之得或，

∴w＝1+7i或w＝－1－7i。