深圳实验学校高中部2005-2006学年度第二学段考试
高二数学(理)试卷
时间:120分钟 满分:150分
第 一 卷(选择题 满分50分)
一、选择题:本大题共10小题,在下列每小题给出的四个结论中有且只有一个正确,请把正确的结论填涂在答题卡上.每小题5分,满分50分.
1.
若命题![]() 的逆命题是
的逆命题是![]() ,命题
,命题![]() 的逆否命题是
的逆否命题是![]() ,则
,则![]() 与
与![]() 的关系是
的关系是
(A)互为逆命题. (B)互为否命题. (C)互为逆否命题. (D)不能确定.
2.
已知正方体![]() 中,点
中,点![]() 是侧面
是侧面![]() 的中心,若
的中心,若![]() ,则
,则![]() 等于
等于
(A)![]() . (B)
. (B)
![]() . (C)
. (C)![]() . (D)
. (D)
![]() .
.
3. 已知![]() 、
、![]() ,则下列各向量中是平面
,则下列各向量中是平面![]() 的一个法向量的是
的一个法向量的是
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
4.
设![]() ,
,![]() ,若命题
,若命题![]() ,命题
,命题![]() ,那么命题
,那么命题![]() 是命题
是命题![]() 的
的
(A)充分不必要条件. (B) 必要不充分条件.
(C) 充要条件. (D)既不充分又不必要条件.
5.
若方程![]() 表示椭圆,则
表示椭圆,则![]() 的取值范围是
的取值范围是
(A)![]() .
(B)
.
(B) ![]() .
.
(C) ![]() .
(D)
.
(D) ![]() .
.
6.
设![]() 为双曲线
为双曲线![]() 的离心率,且
的离心率,且![]() ,则实数
,则实数![]() 的取值范围为
的取值范围为
(A)![]() .
(B)
.
(B)![]() . (C)
. (C)![]() .
(D)
.
(D) ![]() .
.
7.
设![]() 是双曲线
是双曲线![]() 上一点,双曲线的一条渐近线方程为
上一点,双曲线的一条渐近线方程为![]() ,
,![]() 、
、![]() 分别是双曲线的左、右焦点.若
分别是双曲线的左、右焦点.若![]() ,则
,则![]() =
=
(A)![]() 或
或![]() .
(B)
.
(B)![]() .
(C)
.
(C)![]() .
(D)
.
(D)![]() .
.
8.
已知![]() 是椭圆
是椭圆![]() 的半焦距,则
的半焦距,则![]() 的取值范围是
的取值范围是
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
9.
椭圆![]() 的左准线为
的左准线为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,抛物线
,抛物线![]() 的准线为
的准线为![]() ,焦点是
,焦点是![]() ,
,![]() 与
与![]() 的一个交点为
的一个交点为![]() ,则
,则![]() 的值等于
的值等于
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() .
(D)
.
(D)![]() .
.
10. 抛物线![]() 与直线
与直线![]() 交于两点
交于两点![]() 、
、![]() ,其中点
,其中点![]() 的坐标是
的坐标是![]() ,设抛物线的焦点为
,设抛物线的焦点为![]() ,则
,则![]() 等于
等于
(A)![]() . (B)
. (B)![]() . (C)
. (C)![]() . (D)
. (D)![]() .
.
深圳实验学校高中部2005-2006学年度第二学段考试
高二数学(理)试卷
第 二 卷(非选择题 满分100分)
二.填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.
11. 写出命题“![]() ”的否定:
.
”的否定:
.
12. 已知![]() ,
,![]() ,若
,若![]() ,则实数
,则实数![]() = ;若
= ;若![]() ,则实数
,则实数![]() =
.(第
=
.(第![]() 空
空![]() 分,第
分,第![]() 空
空![]() 分)
分)
13. 以双曲线![]() 的对称中心为顶点,双曲线的焦点为焦点的抛物线的方程是
.
的对称中心为顶点,双曲线的焦点为焦点的抛物线的方程是
.
14. 椭圆![]() 的离心率是
的离心率是![]() ,则两准线间的距离为
.
,则两准线间的距离为
.
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15. (本题满分12分)设双曲线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程是
的方程是![]() ,当
,当![]() 为何值时,直线
为何值时,直线![]() 与双曲线
与双曲线![]()
(Ⅰ)有两个公共点?(Ⅱ)仅有一个公共点?(Ⅲ)没有公共点?
16. (本题满分12分)设![]() ,
,![]() ,命题
,命题![]() ,命题
,命题![]() .
.
(Ⅰ)当![]() 时,试判断命题
时,试判断命题![]() 是命题
是命题![]() 的什么条件;
的什么条件;
(Ⅱ)求![]() 的取值范围,使命题
的取值范围,使命题![]() 是命题
是命题![]() 的一个必要但不充分条件.
的一个必要但不充分条件.
17. (本题满分14分)如图,在四棱锥![]() 中,已知底面
中,已知底面![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
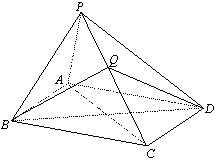 (Ⅱ)求直线
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
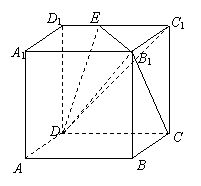
18. (本题满分14分)已知正方体![]() 的棱长为
的棱长为![]() .
.
(Ⅰ)问在棱![]() 上是否存在点
上是否存在点![]() ,使异面直线
,使异面直线![]() 与
与![]() 所成角的余弦为
所成角的余弦为![]() ,若存在,指出点
,若存在,指出点![]() 的位置,若不存在,说明理由;
的位置,若不存在,说明理由;
(Ⅱ)当点![]() 在棱
在棱![]() 上,且
上,且![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
 |
19.
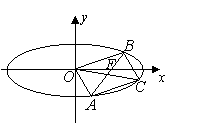
(本题满分14分)已知点![]() ,动点
,动点![]() 到点
到点![]() 的距离比到
的距离比到![]() 轴的距离多
轴的距离多![]() .
.
(Ⅰ)求动点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,过点
,过点![]() 的任意直线与点
的任意直线与点![]() 的轨迹相交于
的轨迹相交于![]() 、
、![]() 两点时,使得线段
两点时,使得线段![]() 的中点到原点
的中点到原点![]() 的距离恒为
的距离恒为![]() 长度的一半?若存在,求出点
长度的一半?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
20.
(本题满分14分)已知椭圆的中心在原点![]() ,焦点在
,焦点在![]() 轴上,过其右焦点
轴上,过其右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,交椭圆于
,交椭圆于![]() 、
、![]() 两点,若椭圆上存在一点
两点,若椭圆上存在一点![]() ,使四边形
,使四边形![]() 为平行四边形.
为平行四边形.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若![]() 的面积为
的面积为![]() ,求这个椭圆的方程.
,求这个椭圆的方程.
 |
深圳实验学校高中部2005-2006学年度第二学段考试
高二数学(理)参考答案
一、选择题:本大题共10小题,在下列每小题给出的四个结论中有且只有一个正确,请把正确的结论填涂在答题卡上.每小题5分,满分50分.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| B | B | D | A | C | D | C | C | B | A |
二.填空题:本大题共4小题,每小题5分,共20分(第12题第![]() 空
空![]() 分,第
分,第![]() 空
空![]() 分).
分).
11.![]() ; 12.
; 12.![]() 、
、 ![]() ;
;
13.![]() ; 14.
; 14.![]() .
.
三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
15.(本题满分12分)设双曲线![]() 的方程为
的方程为![]() ,直线
,直线![]() 的方程是
的方程是![]() ,当
,当![]() 为何值时,直线
为何值时,直线![]() 与双曲线
与双曲线![]()
(Ⅰ)有两个公共点?(Ⅱ)仅有一个公共点?(Ⅲ)没有公共点?
解:把![]() 代入
代入![]() 得:
得:![]() . …………(*)
. …………(*)
当![]() ,即
,即![]() 时,方程(*)为一次方程,只有一解.
时,方程(*)为一次方程,只有一解.
当![]() 且
且![]() ,即
,即![]() 且
且![]() 时,方程(*)有两个不等实根.
时,方程(*)有两个不等实根.
当![]() 且
且![]() ,即
,即![]() 时,方程(*)有两个相等实根.
时,方程(*)有两个相等实根.
当![]() 且
且![]() ,即
,即![]() 或
或![]() 时,方程(*)没有实根.
时,方程(*)没有实根.
因此,(Ⅰ)当![]() 且
且![]() 时,直线
时,直线![]() 与双曲线
与双曲线![]() 有两个公共点;
有两个公共点;
(Ⅱ)当![]() 或
或![]() 时,直线
时,直线![]() 与双曲线
与双曲线![]() 仅有一个公共点;
仅有一个公共点;
(Ⅲ)当![]() 或
或![]() 时,直线
时,直线![]() 与双曲线
与双曲线![]() 没有公共点.
没有公共点.
16.(本题满分12分)设![]() ,
,![]() ,命题
,命题![]() ,命题
,命题![]() .
.
(Ⅰ)当![]() 时,试判断命题
时,试判断命题![]() 是命题
是命题![]() 的什么条件;
的什么条件;
(Ⅱ)求![]() 的取值范围,使命题
的取值范围,使命题![]() 是命题
是命题![]() 的一个必要但不充分条件.
的一个必要但不充分条件.
解:![]() ,
,![]() .
.
(Ⅰ)当![]() 时,
时,![]() .
.
![]() ,
,![]() 当
当![]() 时,有
时,有![]() ,但
,但![]() 时不能得出
时不能得出![]() .
.
因此,命题![]() 是命题
是命题![]() 的必要但不充分条件.
的必要但不充分条件.
(Ⅱ)当![]() 时,
时,![]() ,有
,有![]() ,满足命题
,满足命题![]() 是命题
是命题![]() 的必要但不充分条件.
的必要但不充分条件.
当![]() 时,
时,![]() ,要使
,要使![]() ,须
,须![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,满足命题
,满足命题![]() 是命题
是命题![]() 的必要但不充分条件.
的必要但不充分条件.
因此,![]() 的取值范围是
的取值范围是![]() .
.
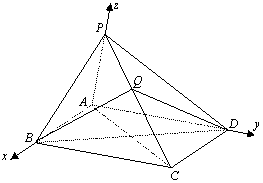
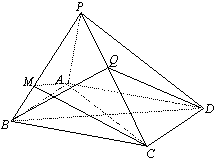 17.(本题满分14分)如图,在四棱锥
17.(本题满分14分)如图,在四棱锥![]() 中,已知底面
中,已知底面![]() 为正方形,
为正方形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅰ)证明:![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 有
有![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
![]()
![]() 底面
底面![]() .
.
![]() ,
,![]() ≌
≌![]() .则由
.则由![]() ,得
,得![]() ,
,
因此,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)法一:过![]() 作
作![]() ,垂足为
,垂足为![]() ,连
,连![]() .
.
![]()
![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,![]() .
.
 又
又![]() ,
,![]()
![]() 平面
平面![]() ,
,![]() ,
,
则![]() 平面
平面![]() .
.
因此,![]() 为
为![]() 与平面
与平面![]() 所成的角.
所成的角.
在直角![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.
法二:依(Ⅰ)可知, ![]() 底面
底面![]() .
.
以![]() 为坐标原点,
为坐标原点, ![]() 、
、![]() 、
、![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,![]() .
.
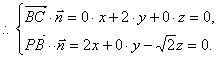 设平面
设平面![]() 的法向量为
的法向量为![]() ,
,
令![]() ,解得
,解得![]() .
.
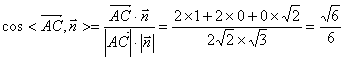
![]() 直线
直线![]() 与平面
与平面![]() 所成角与向量
所成角与向量![]() 和法向量
和法向量![]() 所成角是互余关系.
所成角是互余关系.
![]() 直线
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
18.(本题满分14分)已知正方体![]() 的棱长为
的棱长为![]() .
.
(Ⅰ)问在棱![]() 上是否存在点
上是否存在点![]() ,使异面直线
,使异面直线![]() 与
与![]() 所成角的余弦为
所成角的余弦为![]() ,若存在,指出点
,若存在,指出点![]() 的位置,若不存在,说明理由;
的位置,若不存在,说明理由;
(Ⅱ)当点![]() 在棱
在棱![]() 上,且
上,且![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
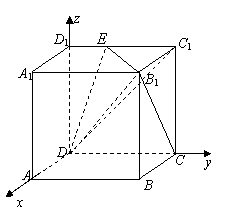 解:(Ⅰ)如图所示,以点
解:(Ⅰ)如图所示,以点![]() 为坐标原点,
为坐标原点,
![]() 、
、![]() 、
、![]() 分别为
分别为![]() 、
、![]() 、
、![]() 轴,
轴,
建立空间直角坐标系.
设存在满足题意的点![]() ,且
,且![]() ,
,
那么![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]()
![]() ,
,![]() .
.
![]()
![]() 与
与![]() 所成角的余弦为
所成角的余弦为![]() ,
,
![]()

![]() ,解得
,解得![]() .
.
![]() 存在点
存在点![]() ,
,![]() 的坐标为
的坐标为![]() 或
或![]() 时,
时,![]() 与
与![]() 所成角的余弦为
所成角的余弦为![]() .
.
(Ⅱ)![]() 平面
平面![]() ,
,![]() 为平面
为平面![]() 的法向量,记为
的法向量,记为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
![]() ,
,![]() ,
,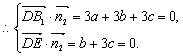
取![]() ,解得
,解得![]() ,故
,故![]() .
.
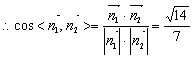 .
.
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.
19.(本题满分14分)已知点![]() ,动点
,动点![]() 到点
到点![]() 的距离比到
的距离比到![]() 轴的距离多
轴的距离多![]() .
.
(Ⅰ)求动点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)在![]() 轴上是否存在这样的点
轴上是否存在这样的点![]() ,过点
,过点![]() 的任意直线与点
的任意直线与点![]() 的轨迹相交于
的轨迹相交于![]() 、
、![]() 两点时,使得线段
两点时,使得线段![]() 的中点到原点
的中点到原点![]() 的距离恒为
的距离恒为![]() 长度的一半?若存在,求出点
长度的一半?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
解:(Ⅰ)依题意,点![]() 到点
到点![]() 的距离等于到直线
的距离等于到直线![]() 的距离,因此点
的距离,因此点![]() 的轨迹是以
的轨迹是以![]() 为焦点,以
为焦点,以![]() 为准线的抛物线,方程为
为准线的抛物线,方程为![]() .
.
(Ⅱ)当线段![]() 的中点到点
的中点到点![]() 的距离为
的距离为![]() 长度的一半时,
长度的一半时,![]() 为直角三角形,
为直角三角形,![]() .
.
假设存在满足条件的点![]() ,点
,点![]() 坐标为
坐标为![]() .
.
当过点![]() 的直线垂直于
的直线垂直于![]() 轴时,依题意有
轴时,依题意有![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
![]() 点
点![]() 在抛物线
在抛物线![]() 上,
上,![]() .
下面证明点
.
下面证明点![]() 满足条件.
满足条件.
当过点![]() 直线不垂直于
直线不垂直于![]() 轴时, 设该直线的斜率为
轴时, 设该直线的斜率为![]()
![]() ,
,
则直线方程为![]() ,又设
,又设![]() 、
、![]() 两点的坐标为
两点的坐标为![]() 、
、![]() .
.
![]()
![]()
![]()
![]() ,
,![]() .……(1)
.……(1)
把![]() 、
、![]() 代入(1)中,得
代入(1)中,得
![]() . ……………(2)
. ……………(2)
由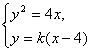 消去
消去![]() ,得
,得![]() ,
,
![]()
![]() .
.
则(2)的左边
![]() .
.
![]() (2)式对任意
(2)式对任意![]() 恒成立.
恒成立.
因此,存在满足条件的点![]() ,点
,点![]() 坐标为
坐标为![]() .
.
 20.(本题满分14分)已知椭圆的中心在原点
20.(本题满分14分)已知椭圆的中心在原点![]() ,焦点在
,焦点在![]() 轴上,过其右焦点
轴上,过其右焦点![]() 作斜率为
作斜率为![]() 的直线
的直线![]() ,交椭圆于
,交椭圆于![]() 、
、![]() 两点,若椭圆上存在一点
两点,若椭圆上存在一点![]() ,使四边形
,使四边形![]() 为平行四边形.
为平行四边形.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若![]() 的面积为
的面积为![]() ,求这个椭圆的方程.
,求这个椭圆的方程.
解:(Ⅰ)设椭圆方程为![]() (
(![]() ),
),
直线![]() ,
,![]() 、
、![]() ,
,![]() 中点为
中点为![]() .
.
由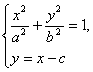 得
得
![]()
![]()
![]() .
.
则![]() ,
,![]() .
.
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,![]()
![]() ,
,![]() .
.
把点![]() 的坐标代入椭圆方程,并化简得
的坐标代入椭圆方程,并化简得![]() ,
,
![]() ,
,![]() 得
得![]() ,即
,即![]() .
.
(Ⅱ)由四边形![]() 为平行四边形,得
为平行四边形,得![]() 的面积等于
的面积等于![]() 的面积.
的面积.
![]() 直线
直线![]() 过焦点
过焦点![]() ,
,![]() 由焦半径公式有
由焦半径公式有
![]()
![]()
![]() , ……………………………(*)
, ……………………………(*)
由![]()
![]()
![]() ,
,![]() ,代入(*),得
,代入(*),得![]() .
.
又![]() 原点到直线
原点到直线![]() 的距离为
的距离为![]() ,
,![]()
![]() 的面积等于
的面积等于![]() .
.
由![]() ,得
,得![]() ,
,![]()
![]() .
.
![]() 椭圆的方程为
椭圆的方程为![]() .
.