南京市汤山中学高二年级数学月考(二)
姓名:___________ 班级:__________ 得分:___________
一、选择题(4*12=48)
1、 若![]() ,则
,则![]() 、
、![]() 、
、![]() 的大小关系为
的大小关系为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、 直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,则
,则![]() 、
、![]() 满足
满足
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3、 在空间,下列命题正确的是 ( )
(A)二组对边分别相等的四边形是平行四边形
(B)四边相等的四边形是平行四边形
(C)有一组对边相等且平行的四边形是平行四边形
(D)两组对角分别相等的四边形是平行四边形
4、 圆![]() 与直线
与直线![]() (
(![]() 且
且![]() )的位置关系是
)的位置关系是
A.相交 B.相切 C.相离 D.不确定
5、 方程x+![]() =0所表示的图形是
=0所表示的图形是
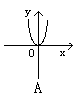
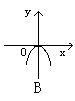
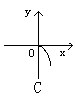

6、 直线y=kx+2与椭圆2x2+3y2=6有两个不同共同点,则有:( )
A.k>![]() B.
B.![]()
C.![]() D.
D.![]()
7、 若关于![]() 的不等式
的不等式![]() 有解,则实数
有解,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、 过点(2,-2)且与双曲线x2-2y2=2有公共渐近线的双曲线方程是( A )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
9、 已知![]() ,则
,则![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、 四个函数:(1)![]() ; (2)y=sinx+
; (2)y=sinx+![]() (0<x<
(0<x<![]() );
);
(3)y=![]() ;(4)
;(4)![]() ,其中最大值为4的函数是( )
,其中最大值为4的函数是( )
A、(1),(2) B、(2),(3) C、(2) D、(4)
11、 原点O到直线![]() 的距离设为
的距离设为![]() ,当正数
,当正数![]() 变动时,
变动时,![]() 的最大值为
的最大值为
A.![]() B.
B.![]() C.1
D.2
C.1
D.2
12、已知P是椭圆![]() 上一点,F1、F2是椭圆的两个焦点,若∠P F
上一点,F1、F2是椭圆的两个焦点,若∠P F
A ![]() B
B
![]() C
C
![]() D
D
![]()
二、填空题(4*6=24分)
13、双曲线![]() 与椭圆
与椭圆![]() 有共同的焦点,则m=
.
有共同的焦点,则m=
.
14、一动圆M和直线l:x= —2相切,且经过点F(2,0),则圆心的轨迹方程是
15.约束条件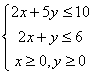 所表示的区域中,整点共有___个
所表示的区域中,整点共有___个
16、被椭圆![]() 内一点P(2,1)平分的弦的斜率为
。
内一点P(2,1)平分的弦的斜率为
。
17、 直角三角形的周长是2,则它的面积的最大值是__________
18.点![]() 在椭圆
在椭圆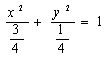 上则
上则![]() 的最小值为____________。
的最小值为____________。
三、解答题(19,20题12分、21、22每题目13分, 23,24题14分)
19、设已知![]() 为正数,(1)求证:
为正数,(1)求证:![]() (2)求证:
(2)求证:![]() ;
;
20、已知B(-5,0),C(5,0)是△ABC的两个顶点,且sinB-sinC=![]() sinA求顶点A的轨迹方程。
sinA求顶点A的轨迹方程。
21、双曲线![]() 的离心率为
的离心率为![]() ,求实数k的值。
,求实数k的值。
22、已知直线![]() 过点
过点![]() ,分别求满足下列条件的
,分别求满足下列条件的![]() 的方程:
的方程:
(1)与坐标轴在第一象限所围成之三角形面积最小;
(2)![]() 在
在![]() 轴、
轴、![]() 轴正半轴上的交点分别为A、B,MA·MB最小。
轴正半轴上的交点分别为A、B,MA·MB最小。
|
24、已知抛物线y2=2px(p>0)与圆(x-2)2+y2=3相交,A、B是它们在x轴上方的交点(如图)若线段AB的中点M在直线y=x上,求p的值。
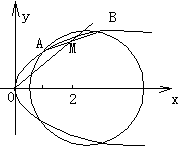 |