排列组合、二项式定理单元测试卷
一、选择题（每题5分，计50分）
1．从7人中选派5人到10个不同交通岗的5个中参加交通协管工作，则不同的选派方法有（ ）
A、
种
B、
种
C、
种 D、
2．某乒乓球队共有男女队员18人，现从中选出男女队员各一人组成一对双打组合，由于男队员中有两人主攻单打项目，不参与双打组合，这样共有64种组合方式，则此队中男队员的人数有（ ）
A、10人 B、8人 C、6人 D、12人
3．设
，则S等于（ ）
A、x4 B、x4+
4．学校要选派4名爱好摄影的同学中的3名参加校外摄影小组的3期培训（每期只派1名），由于时间上的冲突，甲、乙两位同学都不能参加第1期培训，则不同的选派方式有（ ）
A、6种 B、8种 C、10种 D、12种
5．甲、乙、丙三个同学在课余时间负责一个计算机房周一至周六的值班工作，每天1人值班，每人值班2天。如果甲同学不值周一的班，乙同学不值周六的班，则可以排出不同的值班表有（ ）
A、36种 B、42种 C、50种 D、72种
6．(1-2x)7展开式中系数最大的项为（ ）
A、第4项 B、第5项 C、第7项 D、第8项
7．若
展开式中含有常数项，则n的最小值是（ ）
A、4
B、
8．. 一道数学选择题，有四个可供选择的答案，其中有且只有一个答案是正确的，一个学生解答五道这样的数学选择题，每道题都作了选择，问至多有多少种错误情形?( )
A.1021 B.1022 C.1023 D.1024
9．若一个m、n均为非负整数的有序数对（m，n），在做m+n的加法时，各位均不进位则称（m，n）为“简单的有序实数对”，m+n称为有序实数对（m，n）之值。则值为2004的“简单的有序实数对”的个数是（ ）
A、10 B、
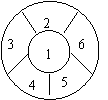10．如图：用四种不同的颜色给标有数字的6个区域染色，
要求相邻的区域不能染同色，则不同的染色方法有（ ）
A、720 B、
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
|
|
|
|
|
|
|
|
|
|
二、填空题（每题4分，计16分）
13．若
，(2-x)n=a0+a1x+a2x2+…+anxn，则a0-a1+a2-…+(-1)nan=_______________________。
14．从10个学生中挑选若干人组成一组，如果必含其中某人的组合数等于必不含某人的组合数，则这样的一个组合的人数有___________________个．
15．计算：
+
+
+……+
=____________________________。
16．3个人坐在一排8个座位上，若每个人的两边都需要有空位，则不同的坐法种数为 ．
三、解答题：
17．（13分）如果a(1-a)4+a2(1+
18．（13分）在1000和9999之间由四个不同数字组成，且个位数字与千位数字之差的绝对值是2的整数个数有多少个？
19．（16分）有3名男生，4名女生，在下列不同要求下，求不同的排列方法总数．
（1）全体排成一行，其中甲只能在中间或者两边位置．
（2）全体排成一行，其中甲不在最左边，乙不在最右边．
（3）全体排成一行，其中男生必须排在一起．
（4）全体排成一行，男、女各不相邻．
（5）全体排成一行，男生不能排在一起．
（6）全体排成一行，其中甲、乙、丙三人从左至右的顺序不变．
（7）排成前后二排，前排3人，后排4人．
（8）全体排成一行，甲、乙两人中间必须有3人．
20．（14分）求
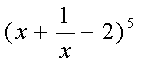展开式中的常数项的值
21．（14分）已知数列
是等比数列，
，公比q是
的展开式的第二项（按x的降幂排列）
（1）求数列的通项
与前n项和
。
（2）若
，求
。
22．（14分）20个不加区别的小球放入编号为1、2、3的三个盒子中，要求每个盒内的球数不小于它的编号数，求不同的放法种数．
排列组合、二项式定理及概率单元试卷答案
一、选择题
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | A | A | D | B | C | A | C | B | C |
二、填空题
| 13 | 14 | 15 | 16 |
| 81 | 5 |
| 120 |
三、解答题
17．由已知得:
，即: 
18．当千位数字分别为：1 2 3 4 5 6 7 8 9
个位数字对应为： 3 0,4 1,5 2,6 3,7 4,8 5,9 6 7
满足条件的四位数有N=
840（个）
19．（14分）解：(1)利用元素分析法，甲为特殊元素，故先安排甲左、右、中共三个位置可供甲选择．有A
种，其余6人全排列，有A
种．由乘法原理得AA=2160种．
(2)位置分析法．先排最右边，除去甲外，有A
种，余下的6个位置全排有A种，但应剔除乙在最右边的排法数A
A
种．则符合条件的排法共有AA－AA=3720种．
(3)捆绑法．将男生看成一个整体，进行全排列．再与其他元素进行全排列．共有A
A=720种．
(4)插空法．先排好男生，然后将女生插入其中的四个空位，共有AA
=144种．
(5)插空法．先排女生，然后在空位中插入男生，共有AA
=1440种．
(6)定序排列．第一步，设固定甲、乙、丙从左至右顺序的排列总数为N，第二步，对甲、乙、丙进行全排列，则为七个人的全排列，因此A
=N×A，∴N =
= 840种．
(7)与无任何限制的排列相同，有A=5040种．
(8)从除甲、乙以外的5人中选3人排在甲、乙中间的排法有A种，甲、乙和其余2人排成一排且甲、乙相邻的排法有A
A．最后再把选出的3人的排列插入到甲、乙之间即可．共有A×A
×A=720种．
20．-
21．（1）q=
，所以
（i）当x=1时，
。
(ii)当
时，
。
（2）(i)当x=1时，＝
(ii)当时，＝
＝
＝
。
22 ．(14分) 解： 首先按每个盒子的编号放入1个、2个、3个小球，然后将剩余的14个小球排成一排，如图，OOOOOOOOOOOOOO，有15个空档，其中“O”表示小球，“”表示空档．将求小球装入盒中的方案数，可转化为将三个小盒插入15个空档的排列数．对应关系是：以插入两个空档的小盒之间的“O”个数，表示右侧空档上的小盒所装有小球数．最左侧的空档可以同时插入两个小盒．而其余空档只可插入一个小盒，最右侧空档必插入小盒，于是，若有两个小盒插入最左侧空档，有C种；若恰有一个小盒插入最左侧空档，有
种；若没有小盒插入最左侧空档，有C
种．由加法原理，有N=
=120种排列方案，即有120种放法．