抛物线（A）
一．选择题：
1． 准线为x=2的抛物线的标准方程是
A.
B. 
C. 
D. 
(答：B)
2． 焦点是（-5，0）的抛物线的标准方程是
A.
B. 
C. 
D. 
(答：C)
3． 抛物线F是焦点，则p表示
A.
F到准线的距离 B.F到准线距离的
B.
C. F到准线距离的
D. F到y轴距离的
（答：B）
4． 动点M（x,y）到点F(4,0)的距离比它到直线x+5=0的距离小1，则点M的轨迹方程是
A.
B. 
C. D. 
(答：D)
5．
若抛物线
的准线方程是x=-3，那么抛物线的焦点坐标是
A.（3，0） B.（2，0） C.1，0） D.（-1，0） （答：C）
6．
点于直线
对称的抛物线的焦点坐标为
A
B
C
D
（答：A）
7．
动点P到直线的距离减去它到
的距离之差等于2，则点P的轨迹是
A直线 B椭圆 C双曲线 D抛物线 （答：D）
8．
抛物线的顶点在原点，焦点在y轴上，抛物线上一点
到焦点的距离为5，则抛物线的准线方程是
A
B
C
D
（答：C）
9．
抛物线
的焦点坐标和准线方程分别为
A
B
C
D
（答：C）
10. 在上有一点P，它到焦点的距离是20，则P点的坐标是
A
B
C
或 D
或
（答：C）
11．
物线
的焦点到准线的距离是
A.10 B.5 C.20 D.
（答：B）
12．
抛物线
的焦点坐标是
A.
B.
C.
D.
(答：D)
二．填空题：
1．
的焦点坐标是
答：
2．
的焦点坐标是 准线方程是 （答：（0，
），
3．
顶点在原点，焦点为（0，-2）的抛物线的方程为 （答：）
4．
抛物线
上一点M到焦点的距离是
，则点M到准线的距离是 点M的横坐标是 （答：
）
5． 一条隧道的顶部是抛物拱形，拱高1.1米，跨度是2.2米，则拱形的抛
物线方程是 （答：
）
6．
抛物线点
到其焦点的距离是5，则p=_______ （答：4）
7．
抛物线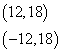
上一点A的纵坐标为4，则点A与抛物线的焦点为_______ （答：5）
三．解答题：
1． 根据下列条件写出抛物线的标准方程
（1）
焦点是F（3，0）
（答：
）
（2）
准线方程是
（答：
）
（3）
焦点到准线距离是2
（答：
）
2．
求顶点在原点，对称轴为坐标轴，过点（2，-8）的抛物线方程，并指出焦点和准线。(
,
3．
抛物线的焦点弦，被焦点分为长为m,n的两部分，求m+n的值。
(答：mn)
4．
正三角形的一个顶点位于坐标原点，另外两个顶点在抛物线
上，求这个正三角形的边长 （答：
）
5．
垂直于
轴的直线交抛物线点A,B,且
，求直线AB的方程 （答：
）
6．
抛物线的顶点在原点，焦点在直线
上，求抛物线的标准方程 （答：
）
抛物线（B）
一．选择题：
1．在直角坐标平面内，到点A(1,1)和到直线x+2y=3的距离相等的点的轨迹
A.直线 B.抛物线 C.圆 D.双曲线 （答：A）
2、线
上到直线2x-y=4的距离最短的点的坐标是
A.
B.(1,1) C. 
D.(2,4)
(答：B)
3、(x0y0)是
上任一点，P到焦点的距离是
A.∣
∣ B.∣
∣ C.∣
∣ D.∣
∣ （答：B）
4、P是抛物线上的点，若P到准线的距离是5，则P点的坐标
是
A.(4,4) B.
C. 
D.
(答：B)
5、方程x2-4x+1=0的两根可分别作为
一椭圆和一双曲线的离心率 B.两抛物线的离心率
C.一椭圆和一抛物线的离心率 D.两椭圆的离心率 （答：A）
6、已知抛物线的焦点为B，点
，T是抛物线上一点，则
的最小值是
A8 B9 C
D10 （答：B）
7、点
到曲线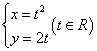
上的点的最短距离为
A0 B1 C
D2 （答：B）
8、与直线
平行的抛物线
的切线的方程是
A
B
C
D
（答：C）
二．填空题：
1．过抛物线
的焦点作倾角为
的弦，此弦的长度是
（答：40）
2. 抛物线
，焦点坐标是（0，-2），则a的值为 （答：1）
3、过抛物线
的焦点作一直线交抛物线于A(x1,y1),B(x1,y1)两点,则
的值是
（答：-4）
4、抛物线被点P（-1，1）平分的弦的直线方程为
（答：4x+y+3=0）
5、在抛物线上顶点和焦点距离相等的点的坐标
是 (答： 
)
6、将抛物线进行平移，使其焦点为
，则此时其顶点坐标为________
（答：22）
7、抛物线
上有一点M，它的横坐标是3，它到焦点的距离是5，则抛物线的方程为_________ （答：）
三．解答题：
1．
求抛物线上各点与焦点连线中点的轨迹方程。
答：
2．
过抛物线的焦点的一条直线与此抛物线相交，两个交点的纵坐标为y1,y2,求y1y2的值。
（答：-p2）
3．
已知动点M到定点A（1，0）与定直线x=3的距离之和等于4，求点M的轨迹方程。 答：
抛物线（C）
一．选择题:
1． 平面上动点P到定点F（1，0）的距离比P到y轴的距离大1，则动点P的轨迹方程为
A.
B.
C. 
D. 
（答：D）
2．
若
,则方程
所表示的曲线一定不是
A.直线 B.圆 C.抛物线 D.双曲线 （答：C）
3．
抛物线
与直线2x-3y-8=0交于M,N两点，线段MN的中点坐标为
A.
B.
C.
D.
(答：A)
4．
抛物线C: 关于直线x+y=2对称的曲线C’的顶点坐标是
A.(0,0) B.(2,2) C.(-2,2) D.(2,0) (答：B)
5．
过抛物线的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点，若x1+x2=6,则∣AB∣得值为
A.10 B.8 C.6 D.4 (答：B)
6．
设抛物线的准线与轴交于点Q，若过Q点的直线L与抛物线有公共点，则直线L的斜率的取值范围是
A
B
C
D
（答：C）
二．填空题：
1．已知圆
与抛物线的准线相切，则p=
（答：2）
2. 以原点为焦点，以x+y-1=0为准线的抛物线方程为
(
)
3．抛物线
上两点A,B到焦点的距离之和是5，则线段AB中点的横坐标是
（答：2）
4． 已知定点A（3，2）在抛物线的内部F为抛物线的焦点，点Q在抛物线上移动，当∣AQ∣+∣QF∣取最小值4时，
p= （答：2）
5．顶点与椭圆
的中心重合，且以椭圆的焦点为焦点的抛物线方程为
（答：
）
6．若双曲线
的一条准线与抛物线的准线重合，则双曲线的离心率为_______ （答：2）
三．解答题：
1．抛物线的顶点在原点，焦点在x轴上，若直线y=2x+1被抛物线截得的弦长为
，求次抛物线方程 。 （答:
）
2．求顶点在原点，以x轴为对称轴，抛物线通径长为8，求抛物线方程
（答:
）
3、已知定点A(3,2)在抛物线的内部，F为抛物线的焦点，点Q在抛物线上移动，当p为何值时∣AQ∣+∣QF∣最小。
（答: 当P=2时∣AQ∣+∣QF∣最小为4）