测试题

1．判断题：（正确的命题在题后括号内画√，错误的命题在题后括号内画×．）

（1）三角形、四边形、圆都是平面图形．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　)

（2）三条平行直线最多可以确定三个平面．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　)

（3）四条边相等的四边形不一定是平面图形．　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

（4）若四点不共面，则任何三点也不共线．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　)

（5）三条直线若两两相交，则三条直线共面．　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　)

2．填空题

（6）平面α经过直线a的充要条件是___________________________________．

（7）“确定一个平面”的充要条件是：______________________________．

（8）两个不同的平面如果有无穷多个公共点，那么这些公共点所在的平面有______个．

3．解答题

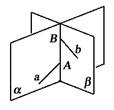
（9）两个平面α和β交于直线l，直线a在α内，直线b在β内，且a，b与l分别交于点A和点B．

试用符号表示上述语句，并画出相应的图形．

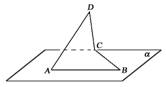
（10）已知如右图

试用文字语言和符号语言说明该图表示的一个几何事实．

（11）求证：两条平行直线确定一个平面．

（12）求证：对角线相交的四边形是平面四边形．

（13）已知：如第（9）题，求证直线a、b相交的充要条件是A、B两点重合．

答案与提示

1．判断题

　　　 （1）×　　　　 （2）√　　　　 （3）√　　　　 （4）√　　　　 （5）×

2．填空题

（6）a上有两个点在平面α内．

（7）略．

（8）无穷多个．

3．解答题

（9），，，，

（10）ABCD是空间四边形，点A、B、C确定平面α，点D在平面α外．点A、B、C∈α，点．

（11）已知：直线a∥b．

求证：经过a、b的平面有且仅有一个

证明：根据平行线的定义，a、b在同一平面α内．

在b上取点B，显然B在a外，

根据推论1，过a和点B，有且只有一个平面，

而过a、b的平面α必过a和B，

因此过a、b的平面只有一个．

综上知，题断正确．

（12）已知：四边形ABCD中，对角线AC、BD相交于点O．

求证：ABCD是平面四边形．

证明：过AC、BD有平面α存在，

于是点A、B、C、D均在α内，

这样AB、BC、CD、DA都在α内，

故ABCD是平面四边形．

（13）充分性：A、B重合，显然a、b相交；

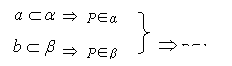必要性：设a、b相交，交点为P

即A、B、P实际上是一个点．

∴ A、B重合．