江苏省西亭高级中学2005-2006学年度第一学期

高二数学期中测试卷

制卷人：朱新星

（全卷满分150分　 考试时间129分钟）

第一卷（选择题共60分）

一．选择题：本大题共12小题，每小题5分，共60分。在每小题给出的四个选项中，只有一项是符合题意要求的。

1．若直线的斜率k= -5，则倾斜角α=　　　　　　　　　　　　　　　 （　）

A．arctan(-5)　　　　　B． π-arctan(-5)　　　C．arctan5　　　　　　　D． π-arctan5

2．直线在两坐标轴上的截距相等，则满足条件是（　 ）

A．　 B．　　C．且　 D．或且　

3．如果l₁,l ₂的斜率分别是二次方程x²-4x+1=0的两根，则l₁,l ₂的夹角是　　 　　(　 )

A．　　　 B.　　C.　　　D.

4． 在下面四个椭圆中，最接近与圆的是　 　　　　　　　　　　　　　　　　（　　）

A.9x²+y²=36　　 B.　　C.　　D.2x²+y²=8

5．是直线和直线平行且不重合的（　　）

　A.充分不必要条件　B.必要不充分条件　C.充要条件　　D. 既不充分也不必要条件

6．到点A（-1，0）和点B（1，0）的斜率之积为-1的动点P的轨迹方程是　　（　　）A．x²+y²=1　　　　　　　　B． x²+y²=1 (x≠±1)

C．x²+y²=1 (x≠0)　　　　　　　　　D．y=

7．若过点P(-2,1)作圆(x-3)²+(y+1)²=r²的切线有且仅有一条，则圆的半径r为　 (　 )

A.29　　 B.　　C.小于 　　　D.大于

8．若椭圆上一点P到右焦点距离为3，则P到左准线的距离为　　　（　　）

　A．　　　　　　 B．　　　　　　  C．2　　　　　　  D．4

9．有一动圆P恒过定点F(a,0)(a>0)且在与y轴相交与点A、B,若△ABP为正三角形，则点P的轨迹为　 　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

A.直线　　　 B.圆　　　　 C.椭圆　　　　  D.双曲线

10．点P（-3,1）在椭圆的左准线上.过点P且方向为a=(2,-5)的光线，经直线y=-2反射后通过椭圆的左焦点，则这个椭圆的离心率为　　　　（　 ）

A.　　　 B.　　　　C.　　　　D.

11．椭圆有这样的光学性质：从椭圆的一个焦点出发的光线，经椭圆反射后，反射光线经过椭圆的另一个焦点. 今有一个水平放置的椭圆形台球盘，点A、B是它的两个焦点，其中焦距为，长轴长为，当放在点A处的小球被击出发，经椭圆壁反弹后再回到点A时，小球经过的路程是　　　　　　　　　　　　　　　　　　　 （　　 ）

　　　 A. 　　　 B. 　　　 C. 　　D.以上答案均有可能

12.已知圆，直线：，和圆交于、两点，以为始边，、为终边的最小正角分别为和．有如下四个命题：

①当和都是常数时，是定值．　　　

②当为常数，是变数时，是定值．

③当为变数，是常数时，是定值．

④当和都是变数时，是定值．

其中正确命题的序号是　　　　　　　　　　　　　　　　　　　　　　 （　　）

A.①、②　　　　　　　　　　　　　　B.②、③　　　　　　　 C.③、④　　　　　　　　　　 D.①、④

第二卷（非选择题共90分）

二、填空题：本大题共6小题，每小题4分，共24分。把答案填在答题卡相应位置。

13. A(0,7)、B(1,10）、C(2,3)、D(-3,5)四点中在直线3x-y+7=0上的点有　　 　　　　　。

14. 若动点分别在直线：和：上移动，则中点到原点距离的最小值为　　　　　　　  。

15. 已知x, y满足约束条件

16.若双曲线的渐近线方程为，它的一个焦点是，则双曲线的方程是__________。

17. 对于椭圆和双曲线有下列命题：

①椭圆的焦点恰好是双曲线的顶点;　②双曲线的焦点恰好是椭圆的顶点;

③双曲线与椭圆共焦点;　　　　　  ④椭圆与双曲线有两个顶点相同.

其中正确命题的序号是　　　　　　  .

18.我们知道若AB是椭圆的不平行于对称轴且不过原点的弦，M为AB的中点，则.在双曲线中是否也有类似的命题？若有，请写出在双曲线中的一个类似的正确命题：　　　　　　　　　　　　　  　　　　　　　　　　　　　  。

三、解答题：本大题共5小题，共66分.解答应写出文字说明、证明过程或演算步骤.

19.（12分）已知以坐标原点为中心的椭圆，满足条件

（1）焦点F₁的坐标为 ( 3, 0 )；

（2）长半轴长为5.

则可求得此椭圆方程为 　　　　　（※）

问可用其他什么条件代替条件（2），使所求得的椭圆方程仍为（※）？请写出两种替代条件，并说明理由。

 

20.（12分）圆x²+y²=8内有一点P₀(-1,2),AB为过点P₀且倾斜角为α的弦。

（1）当时，求AB的长；

(2)当弦AB被点P₀平分时，求AB的方程。

21.（14分）已知与曲线C：相切的直线交的正半轴与两点，O为原点，=a，，．

（1）求线段中点的轨迹方程；

（2）求的最小值．

22.（14分）已知椭圆的一个焦点F₁(0,)，对应的准线方程为y=,且一个顶点的坐标为（0，3）。

（1）求椭圆方程。

（2）是否存在直线l，使l与椭圆交于不同的两点M、N，且线段MN恰被直线x＝平分；若存在求出l的倾斜角的范围，若不存在，请说明理由。

23.(14分)如图，根据指令（γ，θ）（γ≥0，-180°<θ≤180°），机器人在平面上能完成下列动作：先原地旋转角度θ（θ为正时，按逆时针方向旋转θ，θ为负时，按顺时针方向旋转θ），再朝其面对的方向沿直线行走距离γ．

（1）现机器人在平面直角坐标系的坐标原点，且面对x轴正方向．试给机器人下一个指令，使其移动到点（4，4）．

（2）机器人在完成该指令后，发现在点（17，0）处有一小球 正向坐标原点作匀速直线滚动．已知小球滚动的速度为机器人直线行走速度的2倍，若忽略机器人原地旋转所需的时间，问机器人最快可在何处截住小球？并给出机器人截住小球所需的指令（结果用反三角函数表示）．

　　　　　　　　　　　　　　　 

　　　　  　江苏省西亭高级中学2005-2006学年度第一学期

　　　　 　　高二数学期中测试答卷

填空题：

13．　 　　　　　，14．　　　　　　　 ，15．　　　　　　，16．　　　　　　，17． 　　　　　 ，18．　　　　  　　　　　　　　　　　　　　　　　　　　　　。

解答题：

19（12分）：

第一种：

班级　　　　

第二种：

姓名　　　　

考号　　　　 

20（12分）：

（1）

（2）

21（14分）：

（1）

（2）

22（14分）：

（1）

班级　　　　

　　　　　　 （2）

姓名　　　　

考号　　　　

23（14分）：

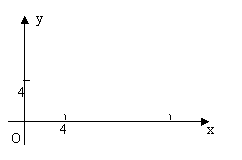（1）

（2）

江苏省西亭高级中学2005-2006学年度第一学期

高二数学期中测试答案

一、选择题

DDCBC,BBCDA,DA

二、填空题

13.A、B; 14.3;15.1;16.;17.①②;18.

三、解答题

19．① 短半轴长为4；

② 离心率 e = ；

③ 右准线方程为 x = ；

④ 点P ( 3, ) 在椭圆上；

⑤ 椭圆上两点间的最大距离为10；

　　　　……

　　（答案是开放的，还可写出多种替换条件.）

20．（1）,　 AB:y=-x+1,  AB=

(2) AB⊥OP₀,AB:x-2y+5=0

21. （1）设AB的中点为P(x,y) ,圆C的方程化简为：

又直线的方程为：，，

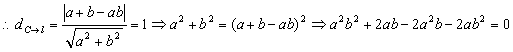
　 ①，

又∵P是AB的中点，

，代入①得，

即线段中点的轨迹方程为；．

（2），

，.∴．

 22.(1).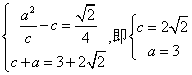

可得椭圆的方程：

（2）令l：y=kx+m,代入椭圆方程得：(k²+9)x²+2kmx+m²-9=0

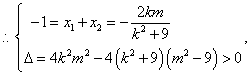解得.

∴倾斜角。

23．（1）如图γ=，θ=，所下指令为（，）

（2）设机器最快在点P（x，0）处截住小球，则因为小球速度是机器人速度的2倍，所以在相同时间内有

即

因为要求机器人最快地去截住小球，即小球滚动距离最短，所以x =7,

故机器人最快可在点P（7，0）处截住小球，

又设Q（4，4），机器人在Q点旋转的角度为

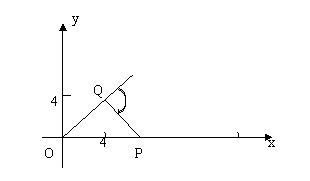则PQ

,

（法一）：由∠QOP=45°，　　

∠QPx=

， -

（法二）：

，

故，所给的指令为（5，）或（5，）